Элементы электрических цепей
Тема 1. Введение в дисциплину.
Основные понятия и определения теории электрических цепей
Электротехника — наука о методах и технических средствах производства, передачи и применения электрической энергии. Электроэнергия — один из видов материальной энергии; она может быть произведена путем преобразования других видов энергии (световой, тепловой, механической, химической), а также используется для производства этих видов энергии.
Промышленная электроника — отрасль электротехники, в которой рассматриваются физические и технические принципы построения электронных приборов и вопросы промышленного применения различных электронных устройств, выполняющих функции управления, контроля, измерения, регулирования.
Теоретические основы электротехники — базовая дисциплина, которая позволяет теоретически исследовать процессы в электромагнитных цепях путем составления их идеализированных моделей (эквивалентных схем замещения) и анализа этих моделей с применением основных законов электродинамики.
1.1 Основные понятия теории цепей
Электрическая цепь — совокупность устройств (элементов, служащих для передачи, распределения или преобразования электромагнитной энергии в цепи), процессы в которых могут быть описаны с помощью понятий тока, напряжения, электродвижущей силы (ЭДС).
Электрический ток — упорядоченное движение электрических зарядов на определенном участке электрической цепи. За положительное направление тока принимается направление движения положительно заряженных частиц.
Величина (сила) тока і отражает скорость изменения заряда q, прошедшего через поперечное сечение проводника в единицу времени t :
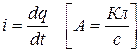 . (1.1)
. (1.1)
Если количество зарядов, проходящих через поперечное сечение проводника в единицу времени, не изменяется, то электрический ток называется постоянным. Переменный ток (или электрический сигнал) является функцией времени, которая может непрерывной или импульсной, с различным законом изменения амплитуды (табл.1.1).
Таблица 1.1 — Виды электрических сигналов
| Электрический сигнал | периодический | непериодический |
| непрерывный | 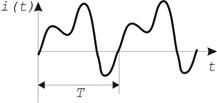 | 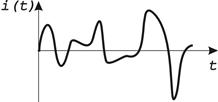 |
| импульсный | 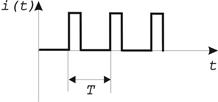 | 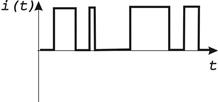 |
Напряжение— количество энергии W, затрачиваемое на перенос единицы заряда из одной точки в другую:
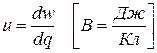 . (1.2)
. (1.2)
Напряжение между точками 1 и 2 электрической цепи есть разность потенциалов φ между этими точками 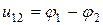 .
.
ЭДС источника энергии Е численно равна работе, совершаемой сторонними силами по перемещению единичного положительного заряда от зажима источника с меньшим потенциалом к зажиму с большим потенциалом.
Энергия, затрачиваемая на перенос заряда q на участке цепи с напряжением и к моменту времени t , может быть определена из (1.2) как
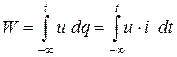 . (1.3)
. (1.3)
Мощность — это скорость изменения энергии во времени. Дифференцируя (1.3) по времени, получаем выражение для определения мощности р
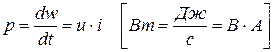 . (1.4)
. (1.4)
1.2 Элементы электрических цепей
Элементы электрической цепи — устройства, входящие в состав цепи и выполняющие в ней определенную функцию. Основными идеализированными элементами электрических цепей являются активные элементы (или источники, вносящие энергию в цепь) и пассивные элементы (или приемники, преобразующие или накапливающие энергию в цепи).
В теории электрических цепей схемные модели пассивных элементов представлены резистивным, емкостным и индуктивным элементами.
Резистивный элемент (сопротивление)— модель устройства, в котором энергия электромагнитного поля необратимо преобразовывается в теплоту. Наиболее близкими по свойствам реальными элементами являются резисторы, электронагревательные элементы.
В соответствии с законом Ома падение напряжения на резистивном элементе uR прямо пропорционально току (табл.1.2), где коэффициент пропорциональности называется сопротивлением R (измеряется в Омах).
В случае, если R=0, то резистивный элемент моделирует короткозамкнутый участок цепи (перемычку). Если же сопротивление бесконечно велико, то резистивный элемент моделирует разомкнутый участок цепи (разрыв).
Величина, обратная сопротивлению 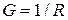 , называется проводимостью (измеряется в Сименсах).
, называется проводимостью (измеряется в Сименсах).
Величина сопротивления и проводимости резистивного элемента R не зависит от закона изменения тока и напряжения в цепи (табл.1.2). В силу закона Ома формы тока и напряжения на резистивном элементе при любом изменении во времени повторяют друг друга: 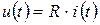 .
.
Мощность, выделяемая на резистивном элементе, является квадратичной функцией тока или напряжения, поэтому она всегда принимает положительные значения. Это означает, что энергия, поступая от источника к резистивному элементу, только потребляется (преобразуется в тепло).
Таблица 1.2 — Параметры пассивных элементов
| Вид элемента | Определение | Напряжение,В | Мощность, Вт | Энергия, Дж |
Резистивный 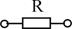 | 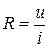 , [Ом] , [Ом]  , [См] , [См] | 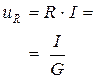 | 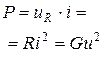 | 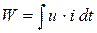 тепловое поле тепловое поле |
Индуктивный 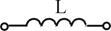 | 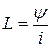 , [Гн] , [Гн] | 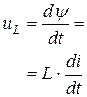 | 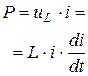 | 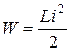 магнитное поле магнитное поле |
Емкостной 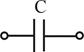 | 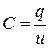 , [Ф] , [Ф] | 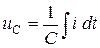 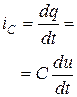 | 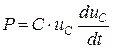 | 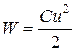 электрич. поле электрич. поле |
Индуктивный элемент (индуктивность)— модель устройства, накапливающего энергию магнитного поля на локальном участке цепи. Наиболее близким по свойствам реальным элементом является катушка индуктивности.
В соответствии с законом электромагнитной индукции падение напряжения на индуктивном элементе uL равно производной потокосцепления ψ по времени, а, значит, пропорционально скорости изменения тока (табл.1.2). Коэффициент пропорциональности называется индуктивностью L (измеряется в Генри). При отсутствии изменения тока величина uL=0, поэтому и L=0, следовательно, индуктивный элемент в цепи постоянного тока эквивалентен короткозамкнутому участку (перемычке).
Приизменении во времени форма тока и напряжения на индуктивном элементе не повторяют друг друга.
Мгновенная мощность, выделяемая на индуктивном элементе (табл.1.1), может иметь разные знаки в зависимости от знака производной тока. Если мощность положительна, то индуктивный элемент потребляет (накапливает) энергию. Если же знак мощности отрицательный, то в этих условиях индуктивный элемент возвращает энергию во внешнюю цепь.
Емкостной элемент (емкость)— модель устройства, накапливающего энергию электрического поля на локальном участке цепи. Наиболее близким по свойствам реальным элементом является конденсатор.
Ток в ветви с емкостным элементом пропорционален скорости изменения заряда, и, соответственно, напряжения uС (табл.1.1). Коэффициент пропорциональности называется емкостью С (измеряется в Фарадах). При отсутствии изменения напряжения ток в ветви с емкостным элементом протекать не будет, поэтому емкостной элемент в цепи постоянного тока эквивалентен разрыву цепи.
Приизменении во времени форма тока и напряжения на емкостном элементе не повторяют друг друга.
Мгновенная мощность, выделяемая на емкостном элементе (табл.1.1), может иметь разные знаки в зависимости от знака производной напряжения. Если мощность положительна, то емкостной элемент потребляет (накапливает) энергию. Если же мощность отрицательна, то емкостной элемент возвращает запасенную энергию во внешнюю цепь.
Рассмотренные выше параметры пассивных элементов (R, L, C) являются константами, т.е. не зависят от величины и направления тока или напряжения. Элементы с такими неизменными параметрами называются линейными. Соответственно, линейными называются и электрические цепи, построенные на линейных элементах.
Реальные электротехнические и электронные приборы могут быть представлены совокупностью линейных элементов лишь в определенных диапазонах изменения тока или напряжения в цепи. В общем случае реальные приборы являются нелинейнымиэлементами, а все электронные устройства представляют нелинейными электрическими цепями.
При теоретическом анализе процессов в электрических цепях источники электромагнитной энергии представляют в виде идеализированных источников напряжения (ЭДС) или тока (токодвижущей силы), которые в схеме изображают активной ветвью-двухполюсником (табл.1.2).
Независимый источник напряжения (ЭДС) — это источник, у которого напряжение на зажимах аb практически не зависит от тока и режима работы присоединенной внешней цепи (табл.1.3). Идеальным можно считать источник ЭДС, у которого внутреннее сопротивление R0 пренебрежимо мало по сравнению с сопротивлением внешней цепи. Если же внутреннее сопротивление соизмеримо с сопротивлением внешней цепи, источник ЭДС называют реальным. Примером источников ЭДС являются гальванические и солнечные батареи, электрические генераторы, аккумуляторы в режиме разрядки.
Таблица 1.3 — Основные параметры источников электроэнергии
| Вид источ-ника | Схемная модель источника | Основные пара-метры | Вольт- Амперная Характерист. | Эквива-лентная замена | Особые режимы работы |
| Ист. ЭДС (напря-жения) Е,[B] | Идеальный 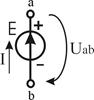 | 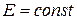 І– любой, R0 = 0 І– любой, R0 = 0 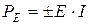 | 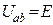 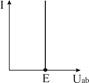 | нет | Холостой ход (Х.Х.) 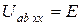 Короткое замыкание (К.З.) Короткое замыкание (К.З.) 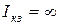 |
Реальный 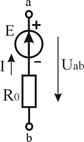 | 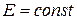 І=0... E/R0 R0 > 0 І=0... E/R0 R0 > 0 | 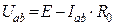 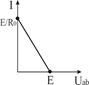 | Ист.тока 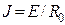 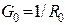 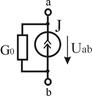 | Х.Х. 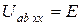 К.З. К.З. 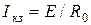 | |
| Ист. ТДС (тока) J, [A] | Идеальный 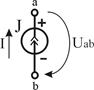 | 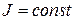 U- любое, G0 = 0 U- любое, G0 = 0 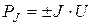 | 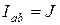 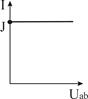 | нет | К.З. 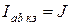 |
Реальный 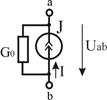 | 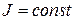 U=0...J/G0 G0 > 0 U=0...J/G0 G0 > 0 | 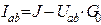 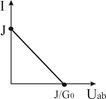 | Ист.ЭДС 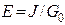 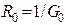 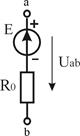 | К.З. 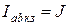 Х.Х. Х.Х. 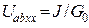 |
Мощность, развиваемая источником ЭДС на участке цепи ab, определяется как 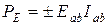 . Величина мощности положительна в случае, если знаки сомножителей совпадают (т.е. совпадают направление действия источника ЭДС и тока в ветви). При противоположных направлениях мощность источника отрицательна, т.е. источник является не генератором, а потребителем энергии (например, аккумулятор в режиме зарядки).
. Величина мощности положительна в случае, если знаки сомножителей совпадают (т.е. совпадают направление действия источника ЭДС и тока в ветви). При противоположных направлениях мощность источника отрицательна, т.е. источник является не генератором, а потребителем энергии (например, аккумулятор в режиме зарядки).
Независимый источник тока (ТДС) — это источник, у которого ток на зажимах аb практически не зависит от величины приложенного к нему напряжения (режима работы присоединенной внешней цепи). Идеальным можно считать источник тока, у которого внутреннее сопротивление R0 намного больше сопротивления внешней цепи. Если же внутреннее сопротивление соизмеримо с сопротивлением внешней цепи, источник тока называют реальным.
Примером источников тока являются устройства, испускающие поток заряженных частиц.
Мощность, развиваемая источником тока на участке цепи ab, определяется как 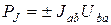 .
.
Из приведенных определений реальных источников ЭДС и тока понятно, что они взаимозаменяемы. Поэтому для упрощения расчетов можно производить эквивалентную замену источников (табл.1.3).
Зависимые источники энергии. Наряду с рассмотренными выше независимыми источниками тока и напряжения существуют зависимые (или управляемые) источники тока и напряжения. Зависимый источник представляет собой элемент с парой входных и парой выходных зажимов (четырехполюсник).
В зависимом источнике входной ток или напряжение является управляющим по отношению к выходному. Входная ветвь источника может быть короткозамкнутая (управляющий ток і1) либо разомкнутая (управляющее напряжение u1), а выходная ветвь представлена источником тока или напряжения. В соответствии с этим различают четыре типа зависимых источников (табл.1.4).
Многие реальные электротехнические и электронные приборы и устройства, служащие источниками электрического сигнала, можно представить приведенными схемами управляемых источников (например, трансформатор — ИНУН, транзистор — ИТУТ).
Таблица 1.4 — Управляемые источники
| Тип | Управляемый напряжением (УН) | Управляемый током (УТ) |
| источник напряже-ния (ИН) | ИН УН 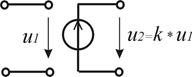 | ИН УТ 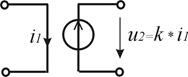 |
| источник тока (ИТ) | ИТ УН 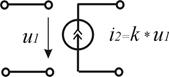 | ИТ УТ 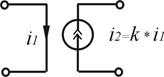 |
1.3 Схема электрической цепи
При теоретическом анализе процессов, происходящих в реальной электрической цепи, необходимо составить ее идеализированную модель, наиболее полно учитывающую свойства соответствующей реальной цепи. Графическое изображение модели реальной цепи называется схемой замещения или просто схемой (рис.1.1). Она отображает как количество и характер элементов, так и их взаимосвязь в цепи. Топологическими элементами схемы являются ветвь, узел, контур.
Ветвь— это участок цепи, содержащий один либо несколько соединенных друг за другом элементов. При этом вдоль одной ветви протекает один и тот же ток.
На рис.1.1 ветвями являются 5 участков: между точками 1-2, 2-3`, 2-3``, 1-3`, 1-3``. Участок 3`-3`` ветвью не является, поскольку в нем нет элементов, он моделирует участок проводника (перемычку). Ветвь 1-2 является активной (содержит источник), остальные ветви схемы — пассивные.
Узел — это точка соединения трех и более ветвей. На рис.1.1 узлами являются три точки — 1, 2 и связанные проводником точки 3`-3`` (узел 3). Узлы 1 и 2 являются сосредоточенными, а узел 3 — распределенный узел.
Контур — это некоторый замкнутый путь вдоль ветвей и узлов схемы. Простейшая цепь состоит из одного контура. На практике чаще рассматриваются многоконтурные схемы. На рис.1.1 кроме отмеченных пунктиром контуров I, II, III, можно определить контуры, проходящие вдоль ветвей схемы через точки 1-2-3``-1, 1-2-3`-3``-1 либо 1-2-3``-3`-1.
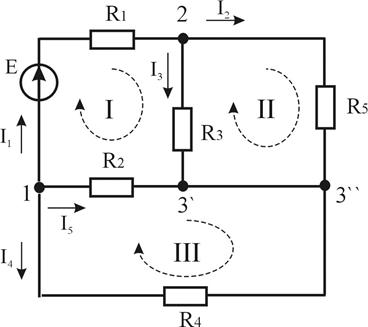
Рисунок 1.1 — Схема электрической цепи
В дальнейшем при анализе цепи нужно уметь определять не все контуры, а лишь необходимое их количество (независимые контуры), охватывая при этом все ветви схемы. Независимым является контур, отличающийся от прежде выбранного контура хотя бы одной новой ветвью. На рис.1.1 отмеченные пунктиром контуры I, II, III являются независимыми (они выбраны по ячейкам схемы). В схеме есть и другие независимые контуры, например I, II, 1-2-3``-1 или II, III, 1-2-3`-3``-1.
1.4 Общая постановка задач в теории электрических цепей
Общая задача анализа электрической цепи состоит в том, что по заданной конфигурации и параметрам цепи (ЭДС, ТДС, сопротивлениям) необходимо рассчитать токи, напряжения на отдельных участках, а также мощность, развиваемую или потребляемую электрической цепью.
Обратная задача (задача синтеза электрической цепи) заключается в определении конфигурации цепи и расчете параметров ее элементов по известным электрическим величинам (токам, напряжениям, мощности).
Для расчета линейных электрических цепей существуют различные аналитические методы, каждый из которых имеет свои преимущества и ограничения. Рациональный выбор расчетного метода определяется свойствами конкретной цепи и постановкой задачи.
Й ВАРИАНТ ГЛАВЫ 1
Тема1 Основные понятия и определения теории электрических цепей
Основные понятия теории цепей
Электрическая цепь — совокупность устройств (элементов, служащих для передачи, распределения или преобразования электромагнитной энергии в цепи), процессы в которых могут быть описаны с помощью понятий тока, напряжения, электродвижущей силы (ЭДС).
Электрический ток — упорядоченное движение электрических зарядов на определенном участке электрической цепи. За положительное направление тока принимается направление движения положительно заряженных частиц.
Величина (сила) тока і отражает скорость изменения заряда q, прошедшего через поперечное сечение проводника в единицу времени t :
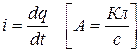 . (1.1)
. (1.1)
Если количество зарядов, проходящих через поперечное сечение проводника в единицу времени, не изменяется, то электрический ток называется постоянным. Переменный ток (или электрический сигнал) является функцией времени, которая может непрерывной или импульсной, с различным законом изменения амплитуды (табл.1.1).
Таблица 1.1 — Виды электрических сигналов
| Электрический сигнал | периодический | непериодический |
| непрерывный | 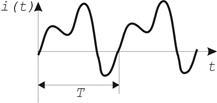 | 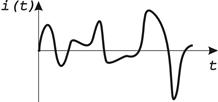 |
| импульсный | 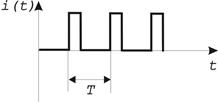 | 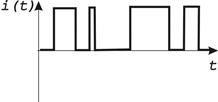 |
Напряжение— количество энергии W, затрачиваемое на перенос единицы заряда из одной точки в другую:
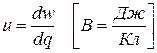 . (1.2)
. (1.2)
Напряжение между точками 1 и 2 электрической цепи есть разность потенциалов φ между этими точками 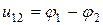 .
.
ЭДС источника энергии Е численно равна работе, совершаемой сторонними силами по перемещению единичного положительного заряда от зажима источника с меньшим потенциалом к зажиму с большим потенциалом.
Энергия, затрачиваемая на перенос заряда q на участке цепи с напряжением и к моменту времени t , может быть определена из (1.2) как
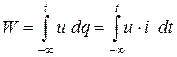 . (1.3)
. (1.3)
Мощность — это скорость изменения энергии во времени. Дифференцируя (1.3) по времени, получаем выражение для определения мощности р
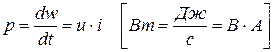 . (1.4)
. (1.4)
Элементы электрических цепей
Элементы электрической цепи — устройства, входящие в состав цепи и выполняющие в ней определенную функцию. Основными идеализированными элементами электрических цепей являются активные элементы (или источники, вносящие энергию в цепь) и пассивные элементы (или приемники, преобразующие или накапливающие энергию в цепи).
В теории электрических цепей схемные модели пассивных элементов представлены резистивным, емкостным и индуктивным элементами.
Резистивный элемент (сопротивление)— модель устройства, в котором энергия электромагнитного поля необратимо преобразовывается в теплоту. Наиболее близкими по свойствам реальными элементами являются резисторы, электронагревательные элементы.
В соответствии с законом Ома падение напряжения на резистивном элементе uR прямо пропорционально току (табл.1.2), где коэффициент пропорциональности называется сопротивлением R (измеряется в Омах).
Величина, обратная сопротивлению 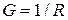 , называется проводимостью (измеряется в Сименсах).
, называется проводимостью (измеряется в Сименсах).
Мощность, выделяемая на резистивном элементе, является квадратичной функцией тока или напряжения, поэтому она всегда принимает положительные значения. Это означает, что энергия, поступая от источника к резистивному элементу, только потребляется (преобразуется в тепло).
Таблица 1.2 — Параметры пассивных элементов
| Вид элемента | Определение | Напряжение,В | Мощность, Вт | Энергия, Дж |
Резистивный 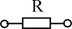 | 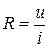 , [Ом] , [Ом]  , [См] , [См] | 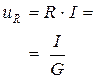 | 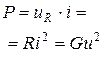 | 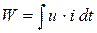 тепловое поле тепловое поле |
Индуктивный 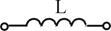 | 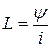 , [Гн] , [Гн] | 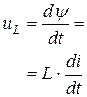 | 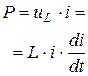 | 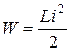 магнитное поле магнитное поле |
Емкостной  | 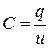 , [Ф] , [Ф] | 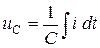 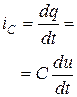 | 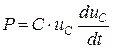 | 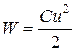 электрич. поле электрич. поле |
Индуктивный элемент (индуктивность)— модель устройства, накапливающего энергию магнитного поля на локальном участке цепи. Наиболее близким по свойствам реальным элементом является катушка индуктивности.
В соответствии с законом электромагнитной индукции падение напряжения на индуктивном элементе uL равно производной потокосцепления ψ по времени, а, значит, пропорционально скорости изменения тока (табл.1.2). Коэффициент пропорциональности называется индуктивностью L (измеряется в Генри). При отсутствии изменения тока величина uL=0, поэтому и L=0, следовательно, индуктивный элемент в цепи постоянного тока эквивалентен короткозамкнутому участку (перемычке).
Мгновенная мощность, выделяемая на индуктивном элементе (табл.1.1), может иметь разные знаки в зависимости от знака производной тока. Если мощность положительна, то индуктивный элемент потребляет (накапливает) энергию. Если же знак мощности отрицательный, то в этих условиях индуктивный элемент возвращает энергию во внешнюю цепь.
Емкостной элемент (емкость)— модель устройства, накапливающего энергию электрического поля на локальном участке цепи. Наиболее близким по свойствам реальным элементом является конденсатор.
Ток в ветви с емкостным элементом пропорционален скорости изменения заряда, и, соответственно, напряжения uС (табл.1.1). Коэффициент пропорциональности называется емкостью С (измеряется в Фарадах). При отсутствии изменения напряжения ток в ветви с емкостным элементом протекать не будет, поэтому емкостной элемент в цепи постоянного тока эквивалентен разрыву цепи.
Мгновенная мощность, выделяемая на емкостном элементе (табл.1.1), может иметь разные знаки в зависимости от знака производной напряжения. Если мощность положительна, то емкостной элемент потребляет (накапливает) энергию. Если же мощность отрицательна, то емкостной элемент возвращает запасенную энергию во внешнюю цепь.
Рассмотренные выше параметры пассивных элементов (R, L, C) являются константами, т.е. не зависят от величины и направления тока или напряжения. Элементы с такими неизменными параметрами называются линейными. Соответственно, линейными называются и электрические цепи, построенные на линейных элементах.
Реальные электротехнические и электронные приборы могут быть представлены совокупностью линейных элементов лишь в определенных диапазонах изменения тока или напряжения в цепи. В общем случае реальные приборы являются нелинейнымиэлементами, а все электронные устройства представляют нелинейными электрическими цепями.
При теоретическом анализе процессов в электрических цепях источники электромагнитной энергии представляют в виде идеализированных источников напряжения (ЭДС) или тока (токодвижущей силы), которые в схеме изображают активной ветвью-двухполюсником (табл.1.2).
Независимый источник напряжения (ЭДС) — это источник, у которого напряжение на зажимах аb практически не зависит от тока и режима работы присоединенной внешней цепи (табл.1.3). Идеальным можно считать источник ЭДС, у которого внутреннее сопротивление R0 пренебрежимо мало по сравнению с сопротивлением внешней цепи. Если же внутреннее сопротивление соизмеримо с сопротивлением внешней цепи, источник ЭДС называют реальным. Примером источников ЭДС являются гальванические и солнечные батареи, электрические генераторы, аккумуляторы в режиме разрядки.
Таблица 1.3 — Основные параметры источников электроэнергии
| Вид источ-ника | Схемная модель источника | Основные пара-метры | Вольт- Амперная Характерист. | Эквива-лентная замена | Особые режимы работы |
| Ист. ЭДС (напря-жения) Е,[B] | Идеальный 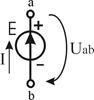 | 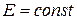 І– любой, R0 = 0 І– любой, R0 = 0 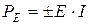 | 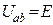 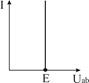 | нет | Холостой ход (Х.Х.) 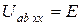 Короткое замыкание (К.З.) Короткое замыкание (К.З.) 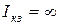 |
Реальный 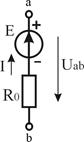 | 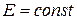 І=0... E/R0 R0 > 0 І=0... E/R0 R0 > 0 | 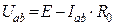 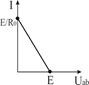 | Ист.тока 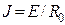 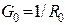 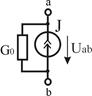 | Х.Х. 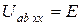 К.З. К.З. 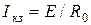 | |
| Ист. ТДС (тока) J, [A] | Идеальный 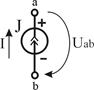 | 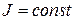 U- любое, G0 = 0 U- любое, G0 = 0 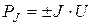 | 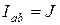 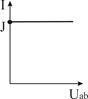 | нет | К.З. 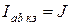 |
Реальный 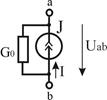 | 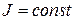 U=0...J/G0 G0 > 0 U=0...J/G0 G0 > 0 | 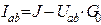 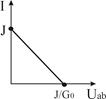 | Ист.ЭДС 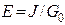 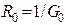 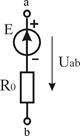 | К.З. 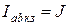 Х.Х. Х.Х. 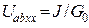 |
Мощность, развиваемая источником ЭДС на участке цепи ab, определяется как 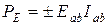 . Величина мощности положительна в случае, если знаки сомножителей совпадают (т.е. совпадают направление действия источника ЭДС и тока в ветви). При противоположных направлениях мощность источника отрицательна, т.е. источник является не генератором, а потребителем энергии (например, аккумулятор в режиме зарядки).
. Величина мощности положительна в случае, если знаки сомножителей совпадают (т.е. совпадают направление действия источника ЭДС и тока в ветви). При противоположных направлениях мощность источника отрицательна, т.е. источник является не генератором, а потребителем энергии (например, аккумулятор в режиме зарядки).
Независимый источник тока (ТДС) — это источник, у которого ток на зажимах аb практически не зависит от величины приложенного к нему напряжения (режима работы присоединенной внешней цепи). Идеальным можно считать источник тока, у которого внутреннее сопротивление R0 намного больше сопротивления внешней цепи. Если же внутреннее сопротивление соизмеримо с сопротивлением внешней цепи, источник тока называют реальным.
Примером источников тока являются устройства, испускающие поток заряженных частиц.
Мощность, развиваемая источником тока на участке цепи ab, определяется как 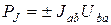 .
.
Из приведенных определений реальных источников ЭДС и тока понятно, что они взаимозаменяемы. Поэтому для упрощения расчетов можно производить эквивалентную замену источников (табл.1.3).
Схема электрической цепи
При теоретическом анализе процессов, происходящих в реальной электрической цепи, необходимо составить ее идеализированную модель, наиболее полно учитывающую свойства соответствующей реальной цепи. Графическое изображение модели реальной цепи называется схемой замещения или просто схемой (рис.1.1). Она отображает как количество и характер элементов, так и их взаимосвязь в цепи. Топологическими элементами схемы являются ветвь, узел, контур.
Ветвь— это участок цепи, содержащий один либо несколько соединенных друг за другом элементов. При этом вдоль одной ветви протекает один и тот же ток.
На рис.1.1 ветвями являются 5 участков: между точками 1-2, 2-3`, 2-3``, 1-3`, 1-3``. Участок 3`-3`` ветвью не является, поскольку в нем нет элементов, он моделирует участок проводника (перемычку). Ветвь 1-2 является активной (содержит источник), остальные ветви схемы — пассивные.
Узел — это точка соединения трех и более ветвей. На рис.1.1 узлами являются три точки — 1, 2 и связанные проводником точки 3`-3`` (узел 3). Узлы 1 и 2 являются сосредоточенными, а узел 3 — распределенный узел.
Контур — это некоторый замкнутый путь вдоль ветвей и узлов схемы. Простейшая цепь состоит из одного контура. На практике чаще рассматриваются многоконтурные схемы. На рис.1.1 кроме отмеченных пунктиром контуров I, II, III, можно определить контуры, проходящие вдоль ветвей схемы через точки 1-2-3``-1, 1-2-3`-3``-1 либо 1-2-3``-3`-1.

Рисунок 1.1 — Схема электрической цепи
В дальнейшем при анализе цепи нужно уметь определять не все контуры, а лишь необходимое их количество (независимые контуры), охватывая при этом все ветви схемы. Независимым является контур, отличающийся от прежде выбранного контура хотя бы одной новой ветвью. На рис.1.1 отмеченные пунктиром контуры I, II, III являются независимыми (они выбраны по ячейкам схемы). В схеме есть и другие независимые контуры, например I, II, 1-2-3``-1 или II, III, 1-2-3`-3``-1.
Для расчета линейных электрических цепей существуют различные аналитические методы, каждый из которых имеет свои преимущества и ограничения. Рациональный выбор расчетного метода определяется свойствами конкретной цепи и постановкой задачи.
