Некоторые основные градационные преобразования
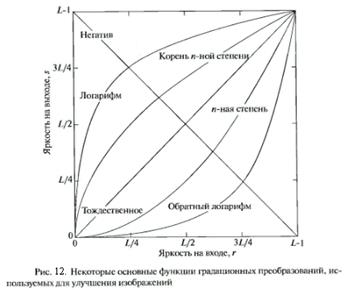
Рис.12 – три основных типа преобразований:
· Линейное (негатив: преобразование ЦИ с яркостями в диапазоне 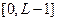 определяется выражением
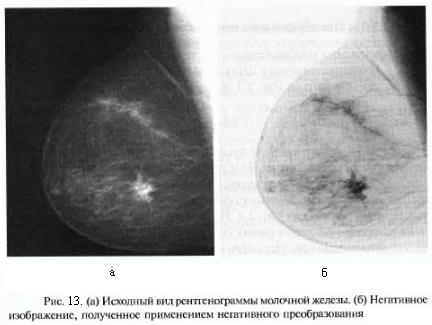
определяется выражением 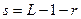 (рис.13); тождественное преобразование:
(рис.13); тождественное преобразование: 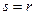 ;
;
· Логарифмическое (общий вид: 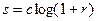 ,
, 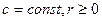 ) ;
) ;
· Степенное (общий вид: 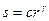 ,
, 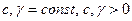 ).
).
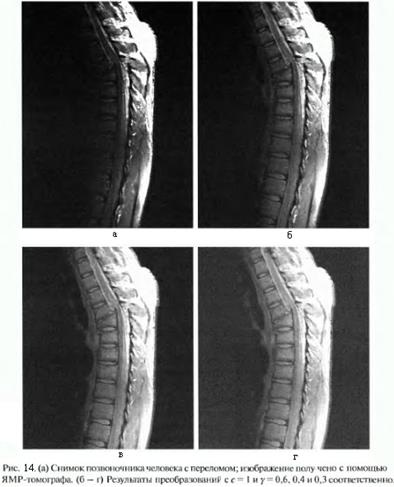
Пример.Улучшение контрастов с помощью степенных преобразований (рис.14). Изображение преимущественно темное, желательно осуществить растяжение уровней яркости. Это может быть достигнуто с помощью степенного преобразования с показателем степени меньше 1.
Пример. Нужно улучшить изображение, которое выглядит «вылинявшим» (рис.15). Это достигается путем степенных преобразований с показателем степени больше 1.

Очень важным объектом, используемым в процессе обработки ЦИ, является его гистограмма. Гистограммой ЦИ с уровнями яркости в диапазоне 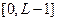 называется дискретная функция
называется дискретная функция 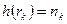 , где
, где 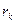 - это
- это 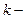 ый уровень яркости, а
ый уровень яркости, а 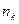 - число пикселей на ЦИ, имеющих яркость
- число пикселей на ЦИ, имеющих яркость 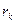 . Общей практикой является нормализация гистограммы путем деления каждого из ее значений на общее число пикселей в ЦИ, обозначаемое
. Общей практикой является нормализация гистограммы путем деления каждого из ее значений на общее число пикселей в ЦИ, обозначаемое 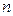 . Тогда значения нормализованной гистограммы будут
. Тогда значения нормализованной гистограммы будут 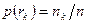 . Сумма всех значений нормализованной гистограммы равна 1. Видоизменение гистограммы может успешно использоваться для улучшения ЦИ.
. Сумма всех значений нормализованной гистограммы равна 1. Видоизменение гистограммы может успешно использоваться для улучшения ЦИ.
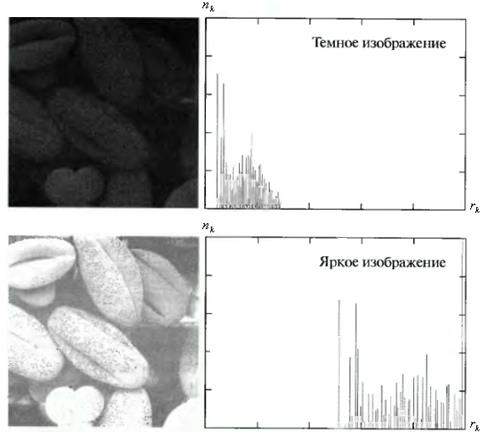
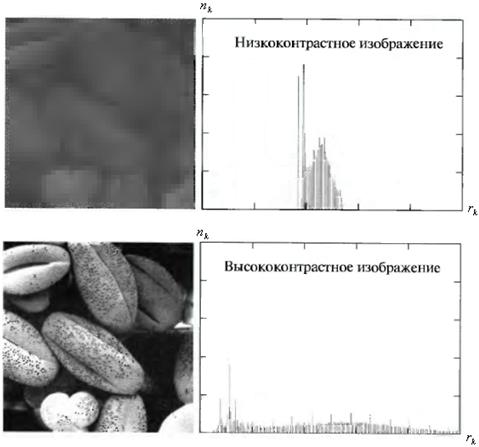
Рис.16. Четыре основных типа изображений
Один из часто используемых способов обработки изображения, которая выполняется с различными целями, является пространственная фильтрация. Пространственная фильтрация – фильтрация, которая выполняется непосредственно над элементами ЦИ. Схема пространственной фильтрации представлена на рис.1.6. Процесс основан на простом перемещении маски фильтра от точки к точке ЦИ; в каждой точке отклик фильтра вычисляется с использованием предварительно заданных связей.
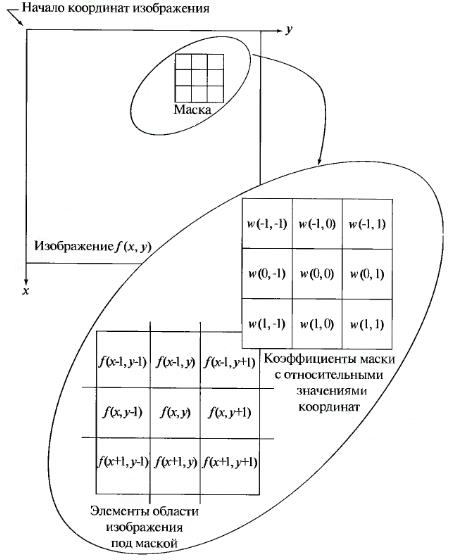
Рис.1.6. Схема пространственной фильтрации
В случае линейной пространственной фильтрации отклик задается суммой произведений коэффициентов фильтра на соответствующие значения пикселей в области, покрытой маской. Для маски 3*3 (рис.1.6), результат (отклик) 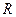 линейной фильтрации в точке
линейной фильтрации в точке 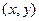 вычисляется как
вычисляется как
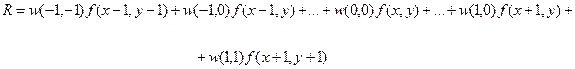
Отклик простейшего линейного сглаживающего пространственного фильтра есть среднее значение элементов по окрестности, покрытой маской фильтра (рис.18). Такие фильтры называют усредняющими или сглаживающими фильтрами. Далее они также будут называться низкочастотными фильтрами. Идея: заменой исходных значений элементов ЦИ на средние значения по маске фильтра достигается уменьшение «резких» переходов уровней яркости, подавление шумов. Однако контуры также характеризуются резкими перепадами яркости, поэтому негативной стороной применения сглаживающих фильтров является расфокусировка контуров, однако такие фильтры позволяют сглаживать ложные контура, которые возникают при преобразованиях с недостаточным числом уровней яркости.
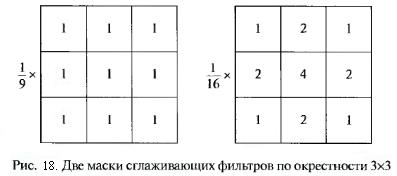
Фильтр, маска которого представлена на рис.18(а) – все коэффициенты одинаковы – наз.однородным усредняющим фильтром. Маска на рис.18(б) дает так называемое взвешенное среднее: коэф-т в центре маски имеет самое большое значение (вес), тем самым давая соответствующему элементу бóльшую важность при вычислении среднего. Значения остальных коэф-тов в маске уменьшается по мере удаления от центра маски. Основная стратегия присвоения центральному пикселю наибольшего веса, а остальным – обратно пропорционально их расстоянию до центра, имеет целью уменьшение расфокусировки при сглаживании.
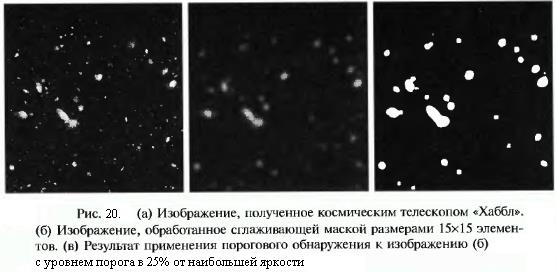
Применение пространственного сглаживания, приводящего к расфокусировке изображения, позволяет создать грубый образ объектов, которые могут представлять интерес. При этом интенсивность мелких объектов смешивается с фоном, в то время как большие объекты остаются в виде пятен и могут быть легко обнаружены. Размеры объектов, которые будут смешиваться с фоном, приблизительно совпадают с размерами маски сглаживающего фильтра. Пример на рис.20. Результат на рис.20(в) является более приемлемым, чем исходное изображение, для задачи поиска самых больших и ярких объектов.
Существуют и другие принципы построения масок фильтров.
Более детально с вопросами, касающимися пространственной фильтрации, видами масок фильтров можно ознакомиться в соответствующем разделе Методических указаний для самостоятельного изучения темы «Принципы построения цифрового изображения и методы его улучшения» по курсу «Стеганография» для студентов специальности 8.04030201 — Информатика (МУ.Стего).
Преобразование Фурье
Прямое преобразование Фурье 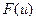 непрерывной функции одной переменной
непрерывной функции одной переменной 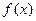 определяется равенством:
определяется равенством:
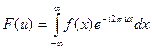 .
.
По заданному преобразованию Фурье 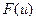 можно получить исходную функцию
можно получить исходную функцию 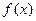 при помощи обратного преобразования Фурье:
при помощи обратного преобразования Фурье:
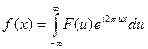 .
.
Для функции двух переменных 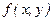 прямое преобразование Фурье
прямое преобразование Фурье 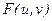 :
:
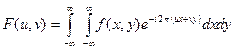 ,
,
Обратное:
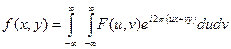 .
.
Преобразование Фурье дискретной функции одной переменной 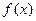 ,
, 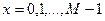 , - дискретное преобразование Фурье (ДПФ) - определяется равенством:
, - дискретное преобразование Фурье (ДПФ) - определяется равенством:
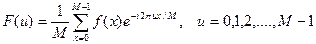 .
.
Исходная функция восстанавливается при помощи обратного ДПФ:
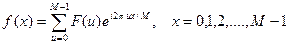 .
.
Понятие частотной области прямо следует из формулы Эйлера: 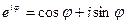 :
:
тогда
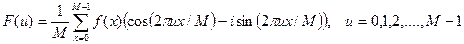 .
.
Таким образом, каждый элемент преобразования Фурье 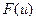 состоит из суммы по всем значениям функции
состоит из суммы по всем значениям функции 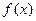 . Значения функции
. Значения функции 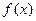 , в свою очередь, умножаются на синусы и косинусы разных частот. Область значений переменной
, в свою очередь, умножаются на синусы и косинусы разных частот. Область значений переменной 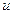 , на которой принимает свои значения функция
, на которой принимает свои значения функция 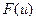 , называется частотной областью, поскольку значения переменной
, называется частотной областью, поскольку значения переменной 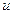 определяют частоты слагаемых, составляющих преобразование. (Значения переменной
определяют частоты слагаемых, составляющих преобразование. (Значения переменной 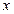 также влияют на частоты, но поскольку по этой переменной производится суммирование, это влияние одинаково для всех значений переменной
также влияют на частоты, но поскольку по этой переменной производится суммирование, это влияние одинаково для всех значений переменной 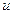 ). Каждый из
). Каждый из 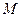 элементов функции
элементов функции 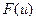 называется частотной компонентой преобразования.
называется частотной компонентой преобразования.
Модулем или спектром Фурье-преобразования называется величина:
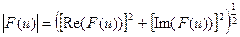 ,
,
Фазой или фазовым спектром:
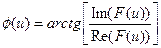 ,
,
Энергетическим спектром называется:
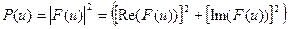 .
.
Дискретное прямое и обратное преобразование Фурье допускает обобщение на двумерный случай. Прямое ДПФ функции 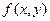 (ЦИ) размерами
(ЦИ) размерами 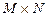 :
:
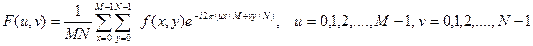 .
.
Обратное ДПФ:
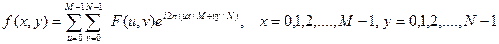 .
.
Переменные 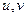 называются частотными переменными, переменные
называются частотными переменными, переменные 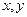 - пространственными переменными или переменными изображения.
- пространственными переменными или переменными изображения.
Фурье-спектр, фаза, энергетический спектр определяются аналогично одномерному случаю:
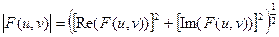 ,
,
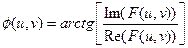 ,
,
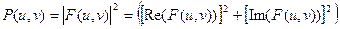 .
.
Значение
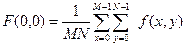
определяет среднее значение функции 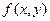 .
.
Обычной практикой является умножение исходной функции (ЦИ) на 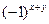 перед вычислением преобразования Фурье. Можно показать, что
перед вычислением преобразования Фурье. Можно показать, что
F 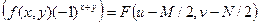 ,
,
Где F – обозначает преобразование Фурье своего аргумента. Это равенство означает, что начало координат для фурье-преобразования функции 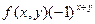 (т.е. та точка, где значение этого преобразования равно
(т.е. та точка, где значение этого преобразования равно 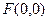 ) находится в точке с координатами
) находится в точке с координатами 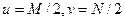 . Другими словами, умножение функции
. Другими словами, умножение функции 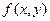 на величину
на величину 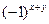 приводит к сдвигу начала координат для ее образа
приводит к сдвигу начала координат для ее образа 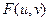 в точку с частотными координатами
в точку с частотными координатами 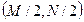 .
.
Далее продемонстрирован результат обработки блока цифрового изображения в среде Matlab.
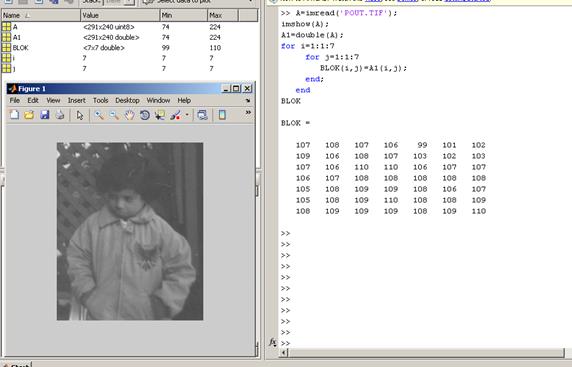
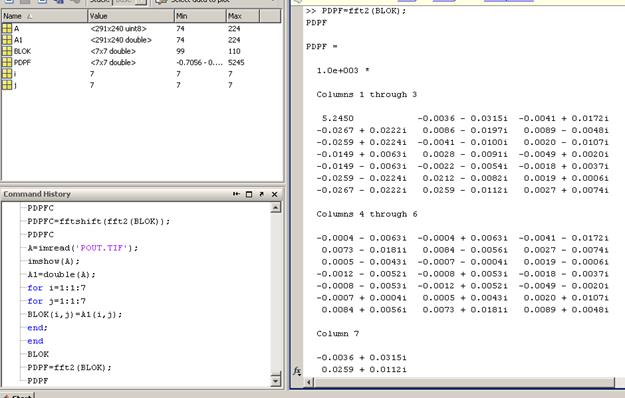
PDPF=
1000*

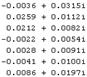
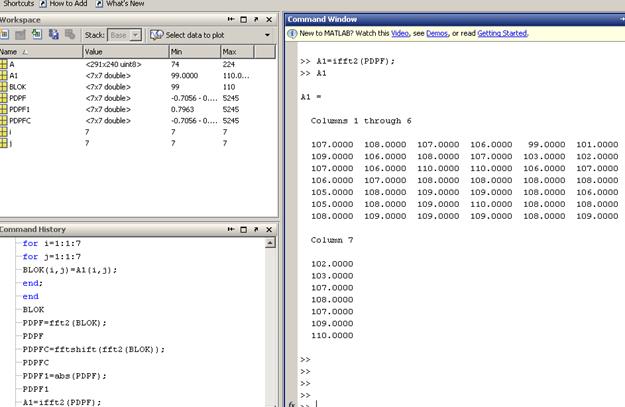
Обратное преобразование Фурье:
Центрирование спектра
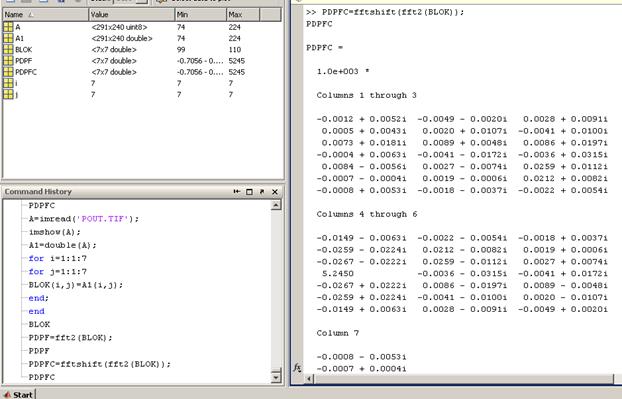
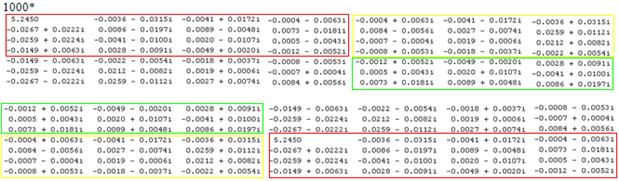
PDPFC=
1000*

Для сравнения матрицы ДПФ и центрированного ДПФ вместе: