Визначення питомого заряду електрона
Методом магнетрона
13.1 Мета роботи
Дослідити рух зарядженої частинки у взаємно перпендикулярних електричному та магнітному полях і визначити питомий заряд електрона 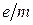 .
.
13.2 Вказівки до організації самостійної роботи
 В даній роботі відношення
В даній роботі відношення 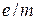 для електрона визначається за допомогою методу, який отримав назву «метод магнетрона». Ця назва пов'язана з тим, що конфігурація електричного і магнітного полів, яка використовується в роботі нагадує конфігурацію полів в магнетронах – генераторах електромагнітних коливань в області надвисоких частот.
для електрона визначається за допомогою методу, який отримав назву «метод магнетрона». Ця назва пов'язана з тим, що конфігурація електричного і магнітного полів, яка використовується в роботі нагадує конфігурацію полів в магнетронах – генераторах електромагнітних коливань в області надвисоких частот.
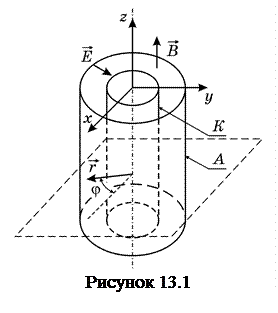
Рух електронів в цьому випадку відбувається в кільцевому просторі, розташованому між катодом і анодом двоелектродної електронної лампи. Нитка розжарювання (катод) розміщується вздовж осі циліндричного анода так, що напруженість електричного поля спрямована вздовж радіуса (рис.13.1). Лампа розміщується всередині соленоїда, який створює магнітне поле, вектор індукції якого паралельний осі катода. Розглянемо траєкторію електро-
нів, які рухаються під дією електричного і магнітного полів. Вважатимемо, що початкова (теплова) швидкість електрона, який вилетів із катода, дорівнює нулю.
Тоді за заданою орієнтацією електричного і магнітного полів рух електрона відбуватиметься в площині, перпендикулярній магнітному полю. Скористаємось полярною системою координат. В цьому випадку положення точки визначається відстанню від осі циліндра 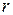 , полярним кутом
, полярним кутом 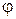 і зсувом уздовж осі Z. Розглянемо спочатку сили, які діють на електрон з боку електричного поля. Напруженість електричного поля в циліндричному конденсаторі має тільки радіальну компоненту Еr. .Тому сила, яка діє на електрон в такому полі спрямована по радіусу так, що
і зсувом уздовж осі Z. Розглянемо спочатку сили, які діють на електрон з боку електричного поля. Напруженість електричного поля в циліндричному конденсаторі має тільки радіальну компоненту Еr. .Тому сила, яка діє на електрон в такому полі спрямована по радіусу так, що
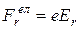 ,
, 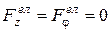 . (13.1)
. (13.1)
Розглянемо тепер сили, які діють на електрон з боку магнітного поля. Оскільки магнітне поле в нашому випадку спрямовано по вісі Z, для проекції сили на вісь Z маємо
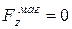 . (13.2)
. (13.2)
Інші дві складові сили знайдемо за допомогою формули Лоренца
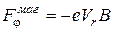 ,
, 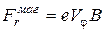 . (13.3)
. (13.3)
З простих кінематичних міркувань зрозуміло, що
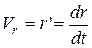 ,
, 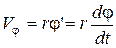 . (13.4)
. (13.4)
Отже, ні магнітні, ні електричні сили, які діють на електрон, не мають складових уздовж осі Z. Рух уздовж осі Z є рівномірним. Рух в площині (r,j) зручно описати за допомогою рівняння моментів
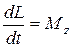 , (13.5)
, (13.5)
де 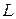 – момент імпульсу електрона відносно осі Z, який дорівнює, як відомо,
– момент імпульсу електрона відносно осі Z, який дорівнює, як відомо, 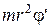 .Величина
.Величина 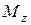 дорівнює
дорівнює 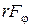 . За допомогою (13.1) і (13.3) знайдемо
. За допомогою (13.1) і (13.3) знайдемо
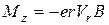 . (13.6)
. (13.6)
Після підстановки (13.4) і (13.6) у (13.5) знайдемо
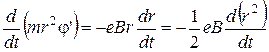 . (13.7)
. (13.7)
Після інтегрування рівняння (13.7) і урахування негативного заряду електрона буде
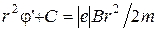 , (13.8)
, (13.8)
де С – стала інтегрування, яку необхідно визначити з початкових умов. На початку руху радіус r дорівнює радіусу катода і є досить малим. Права частина (13.8) і перший член лівої частини також дуже малі. З достатньою точністю можна припустити, що С=0. Тоді рівняння матиме простий вигляд
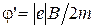 . (13.9)
. (13.9)
Розглянемо тепер рух електрона вздовж радіуса. Робота сил електричного поля , яка виконується під час переміщення електрона від катода до точки з потенціалом U, дорівнює A=eU. Магнітне поле ніякої роботи не виконує. Знайдена робота має дорівнювати кінетичній енергії електрона (початковою швидкістю електрона ми знову нехтуємо)
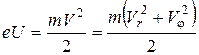 .
.
За допомогою (13.4) і (13.9) знаходимо
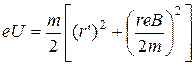 . (13.10)
. (13.10)
 Рівняння (13.10) визначає радіальний рух електрона.
Рівняння (13.10) визначає радіальний рух електрона.
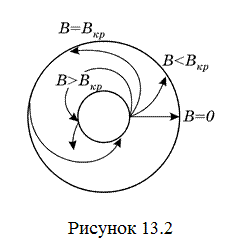
Далі розглядаємо траєкторію електронів, які вилетіли з катода при анодній напрузі 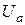 . За відсутності магнітного поля (рис. 13.2) електрони рухаються прямолінійно вздовж радіуса. В слабкому полі траєкторія трохи викривляється, але електрон досягає анода. При збільшенні магнітного поля траєкторія викривляється настільки, що стає дотичною до анода. Це поле називається критичним
. За відсутності магнітного поля (рис. 13.2) електрони рухаються прямолінійно вздовж радіуса. В слабкому полі траєкторія трохи викривляється, але електрон досягає анода. При збільшенні магнітного поля траєкторія викривляється настільки, що стає дотичною до анода. Це поле називається критичним 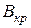 .
.
У випадку 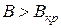 електрон не потрапляє на анод і повертається до катода. Знайдемо величину
електрон не потрапляє на анод і повертається до катода. Знайдемо величину 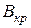 із співвідношення (13.8), звернувши увагу на те, що в цьому випадку радіальна швидкість електрона
із співвідношення (13.8), звернувши увагу на те, що в цьому випадку радіальна швидкість електрона 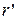 при
при 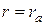 перетвориться на нуль
перетвориться на нуль
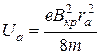 (13.11)
(13.11)
звідки
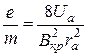 . (13.12)
. (13.12)
Із формули (13.12) знаходимо 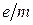 , якщо при заданому
, якщо при заданому 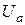 визначене таке значення магнітного поля (або навпаки, при заданому В таке значення
визначене таке значення магнітного поля (або навпаки, при заданому В таке значення 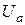 ), при якому електрони перестають потрапляти на анод.
), при якому електрони перестають потрапляти на анод.
13.3 Опис комп’ютерної програми
Зовнішній вигляд інтерфейсу програми зображено на рис. 13.3. Програма базується на модифікованому алгоритмі Ейлера (додаток Б), який описує двовимірний рух електрона в перехрещених магнітному та електричному полях. Програма має основну – “траєкторія” та допоміжному – “Схема та настройки” панелі. В режимі “траєкторія” програма дозволяє вивчити траєкторію руху електрона в широких межах; зміни анодної напруги, величини струму в соленоїді, початкової (теплової) швидкості електрона, з якою він вилітає з катода. Програма також дає можливість спостерігати рух будь-якої кількості електронів, які вилітають із катода з різними початковими швидкостями, прослідкувати вплив на рух електрона (або електронів) просторової густини заряду, який завжди існує в проміжку між анодом та катодом
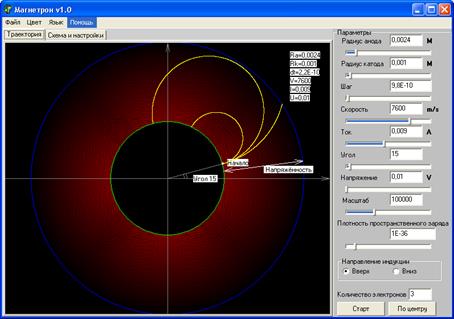
Рисунок 13.3
двоелектродної лампи. В процесі роботи з програмою є також можливість змінювати параметри електронної лампи – радіус катода, анода, регулювати точність обчислень, змінюючи крок переміщення електрона, змінювати масштаб зображення, його положення відносно центра екрана і, нарешті, вибрати приємні кольори зображення траєкторії, анода, катода та електронів.
13.4 Інструкція користувачу
1. Значення об’ємної густини заряду 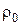 , індукції В (струм котушки), анодної напруги
, індукції В (струм котушки), анодної напруги 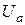 покласти рівними нулю. Значення радіуса анода
покласти рівними нулю. Значення радіуса анода 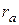 покласти 0,0024 м, радіуса катода – 0,001 м. Початкову швидкість V вибрати відповідно до табл. 13.1. Зарисувати траєкторію руху електрона.
покласти 0,0024 м, радіуса катода – 0,001 м. Початкову швидкість V вибрати відповідно до табл. 13.1. Зарисувати траєкторію руху електрона.
2. Покладіть V=0, анодну напругу 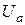 згідно з таблицею. Збільшуючи індукцію (струм котушки) від нуля слід добиватися, щоб електрон пролітав повз анод. Запишіть значення струму
згідно з таблицею. Збільшуючи індукцію (струм котушки) від нуля слід добиватися, щоб електрон пролітав повз анод. Запишіть значення струму 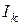 (критичне значення).
(критичне значення).
3. Обчисліть критичне значення індукції 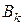 за формулою
за формулою 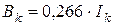 . Результат запишіть в табл. 13.2.
. Результат запишіть в табл. 13.2.
Таблиця 13.1 – Вихідні дані
| Номер вар. | V, м/с | 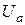 , B , B | Номер вар. | V, м/с | 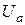 , B , B |
| 2,5 | |||||
| 1,5 | 1,5 | ||||
| 1,2 | |||||
| 1,8 | 2,5 |
Таблиця 13.2 – Результати розрахунків
| Номер | 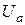 , B , B | 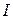 , А , А | 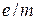 ·10-11, Кл/кг ·10-11, Кл/кг | 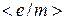 ·10-11, Кл/кг ·10-11, Кл/кг | 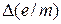 ·10-11, Кл/кг ·10-11, Кл/кг |
4. Повторіть дослід пунктів 3, 4 п’ять разів, збільшуючи кожного разу 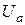 на 0,2В. Отримані дані запишіть в табл. 13.2.
на 0,2В. Отримані дані запишіть в табл. 13.2.
5. Обчисліть відношення 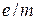 за формулою (13.12), знайдіть його середнє значення і похибку. Похибку визначення
за формулою (13.12), знайдіть його середнє значення і похибку. Похибку визначення 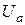 та
та 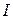 взяти 5%.
взяти 5%.
6. Установіть швидкість електрона, анодну напругу згідно з таблицею. Чому при малих швидкостях траєкторія електрона утворює петлю при збільшенні величини індукції?
7. Змінюючи об’ємну густину заряду 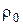 зробіть висновок, як
зробіть висновок, як 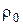 впливає на величину
впливає на величину 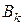 .
.
8. Встановіть початкову швидкість згідно з таблицею, задайте кількість електронів: n=2, 3, 5.
9. Зробіть висновок, як впливає на значення 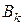 початкова швидкість електронів (в залежності від значення n початкова швидкість 1-го електрона
початкова швидкість електронів (в залежності від значення n початкова швидкість 1-го електрона 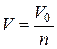 , другого
, другого 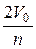 і т.д.).
і т.д.).
13.5 Зміст звіту
Звіт має містити: мету роботи, три зарисовані траєкторії у вигляді прямої, кривої, петлі з поясненнями, чому вони мають такий вигляд, результати у вигляді таблиці, похибки вимірювань, висновки.
13.6 Контрольні запитання і завдання
1. Що являє собою прилад магнетрон?
2. Які сили діють на електрон під час його руху в лампі?
3. Запишіть формулу для сили Лоренца у векторному вигляді.
4. Проаналізуйте формулу для сили Лоренца . Коли сила буде максималь-
на, мінімальна?
5. Який напрямок матиме сила Лоренца на рис.13.1?
6. Якими рівняннями описується рух електрона?
7. Який наближений метод розв’язку рівнянь руху використовується в даній роботі?
ЧАСТИНА IV. ОПТИКА
