Визначення середньої довжини вільного пробігу молекули
4.1 Мета роботи
Ознайомитись з основними положеннями молекулярно-кінетичної теорії (МКТ). Вивчити хаотичний рух молекул, визначити середню довжину вільного пробігу молекул.
4.2 Вказівки до організації самостійної роботи
Двовимірна динамічна модель ідеального газу базується на загальних положеннях МКТ:
1. Всі речовини складаються з молекул (або атомів).
2. Атоми (молекули) знаходяться в стані хаотичного руху.
3. Молекули й атоми взаємодіють між собою. Характер взаємодії зрештою і визначає: чи буде речовина газом, рідиною або твердим тілом.
Внаслідок хаотичного (теплового) руху між молекулами безперервно відбуваються зіткнення. Рухаючись рівномірно і прямолінійно молекула проходить деякий шлях між двома послідовними зіткненнями, який називається довжиною вільного пробігу. Довжина вільного пробігу весь час змінюється. Середня відстань, яку проходить молекула між двома послідовними ударами, має назву середньої довжини вільного пробігу молекули  . Для визначення
. Для визначення  досить розділити шлях, який проходить молекула за 1с, що чисельно дорівнює середній швидкості V, на середню кількість зіткнень
досить розділити шлях, який проходить молекула за 1с, що чисельно дорівнює середній швидкості V, на середню кількість зіткнень 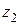 , яких молекула зазнає за 1с:
, яких молекула зазнає за 1с:  =
= 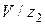 .
.
Для визначення 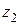 вважатимемо молекулу диском, діаметр якого дорівнює d. Зобразимо шлях диска всередині ламаної смуги шириною 2d (рис.4.1).
вважатимемо молекулу диском, діаметр якого дорівнює d. Зобразимо шлях диска всередині ламаної смуги шириною 2d (рис.4.1).
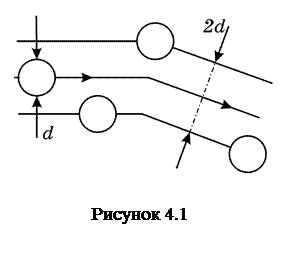 Інші молекули вважаємо нерухомими. Молекула, що рухається, зіткнеться тільки з тими молекулами, центри яких знаходяться на відстанях рівних або менших d. Середня кількість зіткнень
Інші молекули вважаємо нерухомими. Молекула, що рухається, зіткнеться тільки з тими молекулами, центри яких знаходяться на відстанях рівних або менших d. Середня кількість зіткнень 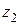 за 1с дорівнює кількості молекул в площі ламаної смуги:
за 1с дорівнює кількості молекул в площі ламаної смуги: 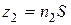 , де
, де  – концентрація молекул (в даному випадку
– концентрація молекул (в даному випадку  – це кількість молекул (дисків), яка припадає на одиницю площі). Площу ламаної смуги можна прирівняти площі спрямленої смуги довжиною V та шириною 2d, отже
– це кількість молекул (дисків), яка припадає на одиницю площі). Площу ламаної смуги можна прирівняти площі спрямленої смуги довжиною V та шириною 2d, отже  . Тоді середня довжина пробігу
. Тоді середня довжина пробігу
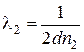 . (4.1)
. (4.1)
Подібні міркування наводять для тривимірної моделі до формули вигляду
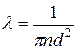 , (4.2)
, (4.2)
де 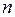 – кількість молекул в одиниці об’єму газу.
– кількість молекул в одиниці об’єму газу.
Порівнюючи формули (4.1) та (4.2) можна встановити зв’язок між довжинами вільного пробігу для дво- та тривимірної моделі
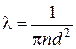 . (4.3)
. (4.3)
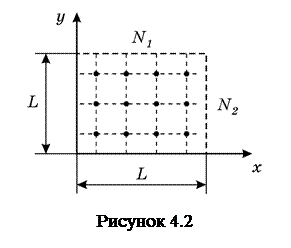
Встановимо зв’язок між  і
і 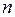 .
.
Визначимо концентрацію молекул  на площині (грані куба) (рис.4.2)
на площині (грані куба) (рис.4.2)
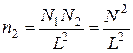 .
.
Якщо розглядати куб з однаковою кількістю молекул в трьох напрямках (рис.4.3), то
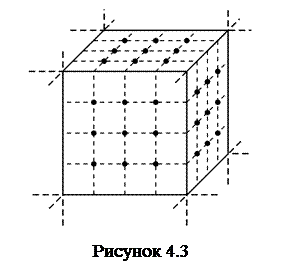
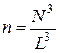 ,
,
тоді
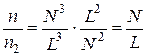 . (4.4)
. (4.4)
Порівнюючи вирази (4.1) та (4.2), можна зробити висновок, що залежність λ від концентрації молекул та розмірів молекули в обох випадках (дво- і тривимірному) залишається однаковою. Як правило, при цьому треба враховувати, що в двовимірному випадку 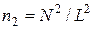 , розміри молекули характеризуються діаметром d, а в тривимірному –
, розміри молекули характеризуються діаметром d, а в тривимірному – 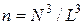 , розміри ~
, розміри ~ 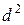 .
.
4.3 Опис комп’ютерної програми
Програма створює такі масиви даних: координати 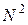 молекул
молекул  ,
, 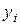 на площині XY та їх початкові складові швидкостей
на площині XY та їх початкові складові швидкостей 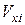 ,
, 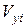 . Початкові швидкості молекул задаються однаковими за величиною та рівними ймовірній швидкості при даній температурі
. Початкові швидкості молекул задаються однаковими за величиною та рівними ймовірній швидкості при даній температурі
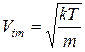 , (4.5)
, (4.5)
де m – маса молекули, T – абсолютна температура, k – стала Больцмана. Ймовірна швидкість (4.5) для двовимірного випадку відрізняється від тривимірного випадку (додаток В). Напрямок швидкості кожної молекули визначається в межах кутів 0...2π за допомогою генератора випадкових чисел. Зовнішній вигляд інтерфейсу програми зображено на рис. 4.4.
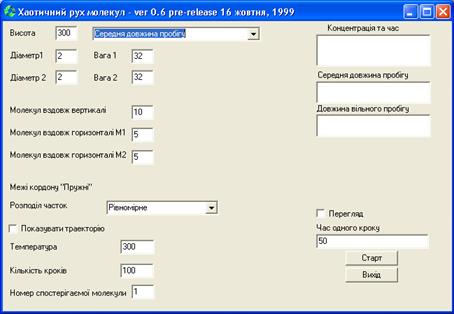
Рисунок 4.4
Розподіл молекул на площині в початковий момент і під час руху відображається на екрані дисплея (рис.4.5). Наступні координати молекул визначаються за кінематичними формулами Ейлера
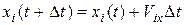 ,
, 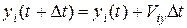 , (4.6)
, (4.6)
 де
де 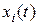 ,
, 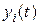 – положення і-ї молекули в момент часу t;
– положення і-ї молекули в момент часу t; 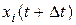 ,
, 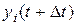 – положення молекули в наступний момент часу
– положення молекули в наступний момент часу 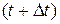 . Зіткнення молекул між собою описується як нецентральний удар твердих пружних кульок. Так називають зіткнення, коли в момент удару початкові швидкості куль
. Зіткнення молекул між собою описується як нецентральний удар твердих пружних кульок. Так називають зіткнення, коли в момент удару початкові швидкості куль 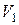 ,
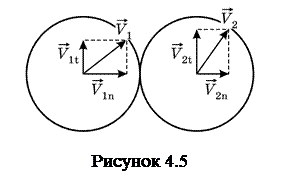
, 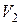 не співпадають за напрямком з лінією, яка з’єднує їхні центри (рис.4.5). Оскільки
не співпадають за напрямком з лінією, яка з’єднує їхні центри (рис.4.5). Оскільки 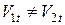 , під час зіткнення розвивалися би сили тертя ковзання, що надало б кулі обертальний рух і тоді енергія поступального руху кульок не зберігалася б. А тому приймаючи удар ідеально пружним, ми вважаємо кульки ідеально гладкими. Під час їх зіткнення тангенціальні сили не виникають, а значить, для тангенціальних швидкостей можна записати
, під час зіткнення розвивалися би сили тертя ковзання, що надало б кулі обертальний рух і тоді енергія поступального руху кульок не зберігалася б. А тому приймаючи удар ідеально пружним, ми вважаємо кульки ідеально гладкими. Під час їх зіткнення тангенціальні сили не виникають, а значить, для тангенціальних швидкостей можна записати
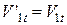 ,
, 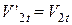 . (4.7)
. (4.7)
У цьому випадку виконуються закони збереження імпульсу та механічної енергії, тоді записуючи ці закони
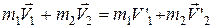 , (4.8)
, (4.8)
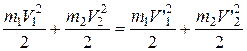 , (4.9)
, (4.9)
де 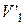 ,
, 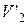 – швидкості кульок після удару, для нормальних складових швидкостей після удару, маємо такі співвідношення:
– швидкості кульок після удару, для нормальних складових швидкостей після удару, маємо такі співвідношення:
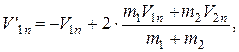
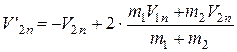 .
.
4.4 Інструкція користувачу
1. Встановити режим роботи програми „Середня довжина пробігу”, вибрати „Розподіл частинок – рівномірний”, ввімкнути „Перегляд”, „Показати траєкторію”.
2. Задати числові дані відповідно до номера варіанта завдання, згідно з табл. 4.1, де маса молекули m вибирається однаковою «Маса 1», «Маса 2», 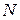 – кількість молекул уздовж осі («Уздовж вертикалі»),
– кількість молекул уздовж осі («Уздовж вертикалі»), 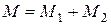 , (
, ( 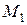 – кількість молекул в першій половині площини,
– кількість молекул в першій половині площини, 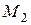 – кількість молекул в другій половині площини уздовж осі х – вибираються однаковими
– кількість молекул в другій половині площини уздовж осі х – вибираються однаковими 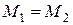 ), d – діаметр молекули («Діаметр 1», «Діаметр 2» – вибираються однакові), Т – температура. Задайте «Кількість кроків» – 1000.
), d – діаметр молекули («Діаметр 1», «Діаметр 2» – вибираються однакові), Т – температура. Задайте «Кількість кроків» – 1000.
Таблиця 4.1 – Вихідні дані
| Номер вар. | ||||||||||||
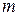 | ||||||||||||
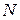 | ||||||||||||
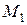 | ||||||||||||
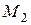 | ||||||||||||
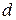 |
3. Спостерігати хаотичний рух молекул і траєкторію виділеної молекули (вона виділяється синім кольором).
4. Для прискорення вимірювань вимкнути «Перегляд» та «Показати траєкторію». Обчислити середню довжину вільного пробігу для ваших даних (кнопка «Старт»). Не змінюючи вихідних даних повторити вимірювання чотири рази. Результати записати в табл. 4.2.
5. Повторити п.4 ще для шести значень діаметра, збільшуючи його від початкового значення з кроком 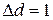 (10-10м). Програма видає середнє значення довжини вільного пробігу молекули, перераховане для тривимірної моделі. Результати записати до табл. 4.2.
(10-10м). Програма видає середнє значення довжини вільного пробігу молекули, перераховане для тривимірної моделі. Результати записати до табл. 4.2.
Таблиця 4.2 – Результати розрахунків
| Номер | 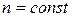 | 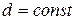 | ||||||||||||||||
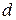 | 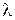 ·10-9, м ·10-9, м | 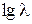 | 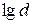 | 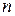 ·1024, м-3 ·1024, м-3 | 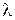 ·10-9, м ·10-9, м | 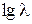 |  | |||||||||||
| <l> | Dl | <l> | Dl | |||||||||||||||
6. Встановити числові дані всіх величин згідно з таблицею 4.1 і номера варіанта.
7. Збільшуючи концентрацію молекул шляхом зміни чисел N і M одночасно від початкових значень з кроком 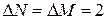 , отримати сім значень
, отримати сім значень 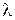 для семи значень концентрації
для семи значень концентрації 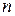 при сталому значенні діаметра молекул
при сталому значенні діаметра молекул 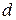 (згідно з таблицею 4.1 і номером варіанта). Записати в табл. 4.2.
(згідно з таблицею 4.1 і номером варіанта). Записати в табл. 4.2.
8. За підрахованими значеннями логарифмів величин побудувати графіки в логарифмічному масштабі: 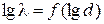 при
при 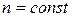 і
і 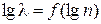 при
при 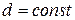 .
.
9. Порівняти результати, отримані з модельного експерименту, з теоретичними. За теоретичною формулою (4.2), беручи десятковий логарифм, маємо для 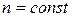 :
:
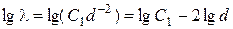 ,
,
 де
де 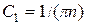 , тобто лінійна залеж-
, тобто лінійна залеж-
ність 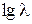 як функції від аргументу
як функції від аргументу 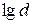 , коефіцієнт нахилу якої дорівнює
, коефіцієнт нахилу якої дорівнює 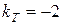 . Якщо з експериментального графіка
. Якщо з експериментального графіка 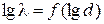 визначити коефіцієнт нахи-
визначити коефіцієнт нахи-
лу 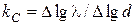 (рис.4.6), то з порів-
(рис.4.6), то з порів-
няння 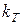 і
і 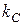 можна зробити висновок, як узгоджуються теоретичні результати
можна зробити висновок, як узгоджуються теоретичні результати
з експериментальними (як залежить 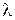 від
від 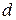 ). Аналогічно перевірити, як залежить
). Аналогічно перевірити, як залежить 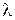 від
від 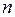 . Зробити висновки.
. Зробити висновки.
4.5 Зміст звіту
Звіт має містити: мету роботи, результати вимірювань, зведені в таблиці, похибки вимірювань, графіки залежностей 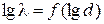 при
при 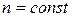 і
і 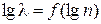 при
при 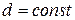 , висновки.
, висновки.
4.6 Контрольні запитання і завдання
1. Сформулюйте три основні положення МКТ.
2. Що таке довжина вільного пробігу молекули?
3. Що таке середня довжина вільного пробігу молекули?
4. Як визначається середня довжина вільного пробігу 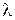 у двовимірній моделі хаотичного руху?
у двовимірній моделі хаотичного руху?
5. Як визначається 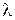 у тривимірній моделі?
у тривимірній моделі?
6. Як пов’язані концентрації молекул у двовимірній і тривимірній моделях?
7. Який удар тіл називається нецентральним?
8. Як записується закон збереження імпульсу при пружному ударі двох кульок?
9. Як записується закон збереження енергії при пружному ударі двох кульок?
10. Якими формулами обчислюються подальші значення координат молекули через попередні?
