Задача 8. Використовуючи властивості якобіанів (1.4), (1.6), довести співвідношення

Розв’язання. Ліву частину цієї рівності можна зобразити у вигляді  Розглядаючи внутрішню енергію
Розглядаючи внутрішню енергію 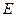 як функцію
як функцію 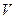 і
і 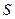 , запишемо
, запишемо

Порівнюючи з формулою (3.13) знаходимо, що 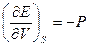 і
і 
Отже, маємо

Використовуючи результат задачі 1 цього розділу, остаточно отримуємо

що й потрібно було довести.
Задача 9. Довести, що для системи, внутрішня енергія якої не залежить від об’єму 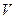 , сам об’єм залежить лише від відношення
, сам об’єм залежить лише від відношення  .
.
Розв’язання. Згідно з (3.19), враховуючи умову  маємо
маємо
 (1)
(1)
Вважатимемо об’єм 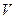 функцією
функцією  і
і 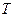 . Тоді
. Тоді

Підставляючи цю похідну в (1), знаходимо:  Використовуючи результати задачі 2 з розділу 1, для трійки змінних
Використовуючи результати задачі 2 з розділу 1, для трійки змінних  можна записати
можна записати

звідки одразу отримуємо (через те, що  )
)

Аналогічно, розглядаючи 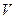 як функцію
як функцію  і
і 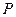 , переконуємося, що
, переконуємося, що

З двох останніх рівностей випливає, що в умовах задачі об’єм 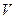 є строго функцією
є строго функцією  .
.
Задача 10. Для ізотермічного і адіабатного модулів пружності довести співвідношення

Розв’язання. За визначенням (0.27) і (0.28) маємо  і
і  Отже,
Отже,

Мовою якобіанів цю рівність можна представити у вигляді
 (1)
(1)
З іншого боку, відношення  на підставі результатів задачі 1 цього розділу дорівнює
на підставі результатів задачі 1 цього розділу дорівнює

або, використовуючи якобіани,
 (2)
(2)
Порівнюючи праві частини в (1) і (2), переконуємося в шуканій рівності

Задачі для самостійного розв’язування
3.1. Довести співвідношення

3.2. Довести співвідношення для різниці теплоємностей

де  термічні коефіцієнти.
термічні коефіцієнти.
3.3. Довести співвідношення

3.4. Довести, що ізотерма не може двічі перетнути адіабату.
3.5. Яка залежність внутрішньої енергії 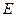 газу від об’єму
газу від об’єму 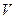 при постійній температурі, якщо термічне рівняння стану описується рівністю Бертло (0.16)?
при постійній температурі, якщо термічне рівняння стану описується рівністю Бертло (0.16)?
3.6. Знайти зміну ентропії системи у випадку її розширення при постійному тиску.
3.7. Довести, що для системи, внутрішня енергія якої не залежить від об’єму, різниця теплоємностей 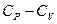 залежить тільки від відношення
залежить тільки від відношення  .
.
3.8. Два гази з фіксованими об’ємами і постійними теплоємностями 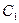 і
і 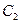 знаходяться в початкових станах з температурами
знаходяться в початкових станах з температурами 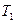 і
і 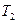
 відповідно. Знайти вираз для температури
відповідно. Знайти вираз для температури  яка встановлюється в результаті прямого теплообміну між газами. Визначити зміну ентропії при цьому і показати, що
яка встановлюється в результаті прямого теплообміну між газами. Визначити зміну ентропії при цьому і показати, що 
3.9.Знайти рівняння адіабати для речовини, термічне рівняння стану якої має вигляд 

3.10.Обчислити різницю молярних теплоємностей  газу, термічне рівняння стану якого описується рівнянням Бертло (0.16), залишаючи лише лінійні члени по відношенню до сталих a і b.
газу, термічне рівняння стану якого описується рівнянням Бертло (0.16), залишаючи лише лінійні члени по відношенню до сталих a і b.
Розділ 4
КОЕФІЦІЄНТ КОРИСНОЇ ДІЇ (ККД) ЦИКЛІВ.
ЦИКЛ КАРНО
Теоретичні відомості
ККД циклів. За визначенням ККД  теплового двигуна (циклу) називається відношення роботи
теплового двигуна (циклу) називається відношення роботи 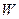 , що здійснюється машиною за цикл, до кількості теплоти
, що здійснюється машиною за цикл, до кількості теплоти  , отриманою робочим тілом машини за цей цикл:
, отриманою робочим тілом машини за цей цикл:
 (4.1)
(4.1)
Якщо позначити через 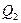 кількість теплоти, яку робоче тіло віддає за цикл, то за першим началом
кількість теплоти, яку робоче тіло віддає за цикл, то за першим началом

звідки
 (4.2)
(4.2)
На підставі (3.4) можна також записати
 (4.3)
(4.3)
тут у знаменнику  підкреслюється, що
підкреслюється, що  кількість теплоти саме на тій ділянці циклу, де
кількість теплоти саме на тій ділянці циклу, де 
Цикл Карно. Теореми Карно. В 20-х роках ХІХ ст. при дослідженні шляхів підвищення ККД теплових машин Саді Карно сформулював дві теореми, які сумісно еквівалентні другому началу термодинаміки.
Перша теорема стосується так званого циклу Карно, який складається з двох ізотермічних  і двох адіабатичних
і двох адіабатичних  процесів. ККД цього циклу легко розраховується за допомогою формули (4.3) і дає:
процесів. ККД цього циклу легко розраховується за допомогою формули (4.3) і дає:
 (4.4)
(4.4)
де 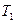 і
і  характеристики двох ізотерм циклу, тобто відповідно температури тепловіддавача (нагрівача) і теплоприймача (холодильника). Перша теорема Карно випливає з цього результату і разом з ним має формулювання: ККД циклу Карно не залежить від природи робочої речовини і граничних адіабат
характеристики двох ізотерм циклу, тобто відповідно температури тепловіддавача (нагрівача) і теплоприймача (холодильника). Перша теорема Карно випливає з цього результату і разом з ним має формулювання: ККД циклу Карно не залежить від природи робочої речовини і граничних адіабат  і
і  , а визначається лише температурами
, а визначається лише температурами 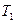 і
і 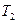 .
.
Важливо зазначити, що вплив температур 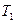 і
і 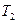 на ККД
на ККД  різний. З (4.4) легко показати, що
різний. З (4.4) легко показати, що
 (4.5)
(4.5)
тобто ця теорема вказує і оптимальні шляхи підвищення ККД, пов’язані зі зменшенням 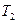 .
.
Друга теорема Карно стверджує, що при однакових значеннях  ККД необоротного циклу менший за ККД оборотного. Це пов’язано з явищем компенсації, в результаті якого частина теплоти при необоротному процесі іде на нагрівання навколишніх тіл.
ККД необоротного циклу менший за ККД оборотного. Це пов’язано з явищем компенсації, в результаті якого частина теплоти при необоротному процесі іде на нагрівання навколишніх тіл.
Зазначимо, що на практиці жодна теплова машина не працює за циклом Карно. Однак його значення полягає в тому, що він визначає максимальний ККД при даних температурних межах циклу.
Нагадаємо також, що в координатах  і
і  робота
робота
 (4.6)
(4.6)
що здійснена системою за цикл, буде додатною при спрямованості обходу контуру в інтегралах (4.6) за годинниковою стрілкою.
