Задача 7. Знайти статистичний інтеграл , внутрішню енергію і теплоємність ультрарелятивістського газу з законом дисперсії для окремої частинки, де – швидкість світла
Розв’язання. У межах канонічного розподілу Гіббса статистичний інтеграл  для ультрарелятивістськього ідеального газу запишемо як
для ультрарелятивістськього ідеального газу запишемо як
 .
.
Конфігураційний інтеграл  ідеального газу дорівнює:
ідеального газу дорівнює:  . Отже, переходячи до сферичних координат
. Отже, переходячи до сферичних координат  , матимемо
, матимемо
 . (1)
. (1)
Внутрішня енергія  розраховується через статистичний інтеграл за формулою
розраховується через статистичний інтеграл за формулою
 . (2)
. (2)
Тому, підставляючи (1) в (2), остаточно знаходимо:

та
 .
.
Задача 8. Система являє собою стовп висотою і перетином одноатомного ідеального газу з частинок, які знаходяться в однорідному полі тяжіння з напруженістю . Визначити у граничних випадках: , .
Розв’язання. У нашому випадку повна енергія системи має вигляд
 ,
,
де  – висота і-ї молекули газу. Для такої системи статистичний інтеграл Z можна записати у вигляді
– висота і-ї молекули газу. Для такої системи статистичний інтеграл Z можна записати у вигляді
 ,
,
що дає
 .
.
Внутрішню енергію  системи знаходимо за формулою (2) попередньої задачі:
системи знаходимо за формулою (2) попередньої задачі:
 . (1)
. (1)
Отже, з (1) маємо
 . (2)
. (2)
Математичний аналіз точного результату (2) у граничних випадках дає:
1) при 
 ,
,
2) при 
 .
.
Як бачимо, перший граничний випадок призводить до класичного значення 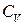 для одноатомного ідеального газу у відсутності зовнішнього поля, що зрозуміло, оскільки при цьому припущенні поле тяжіння не впливає на рух частинок системи.
для одноатомного ідеального газу у відсутності зовнішнього поля, що зрозуміло, оскільки при цьому припущенні поле тяжіння не впливає на рух частинок системи.
У другому випадку можна було б скористатися теоремою про віріал, що дало б такий самий результат. До речі, у першому випадку ця теорема не працює, оскільки не виконується вимога:  при
при  .
.
Задачі для самостійного розв’язування
12.1. За допомогою канонічного розподілу Гіббса показати, що диференціальний вираз для елемента кількості теплоти  має інтегрувальний множник, і знайти цей множник.
має інтегрувальний множник, і знайти цей множник.
12.2. Показати, що для класичного одноатомного газу з  частинок, енергія якого може змінюватися у вузькому інтервалі
частинок, енергія якого може змінюватися у вузькому інтервалі  біля значення
біля значення 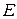
 , ентропію можна зобразити у вигляді
, ентропію можна зобразити у вигляді
 ,
,
де  – коефіцієнт, що залежить від
– коефіцієнт, що залежить від  .
.
12.3. Показати, що отриманий у попередній задачі вираз для ентропії ідеального газу, узгоджується з отриманим в термодинаміці (формула (3.27)).
12.4. Два тіла з постійними температурами  ○С і
○С і  ○С вступають у теплообмін, завдяки якому більш холодне тіло отримало кількість теплоти
○С вступають у теплообмін, завдяки якому більш холодне тіло отримало кількість теплоти  Дж. Знайти:
Дж. Знайти:
а) зміну ентропії системи;
б) зміну термодинамічної імовірності стану (числа доступних мікростанів) системи  .
.
12.5. Відповідно до умови попередньої задачі знайти ймовірність зворотного переходу кількості теплоти  Дж від холоднішого тіла до теплішого. Розглянути також випадок, коли
Дж від холоднішого тіла до теплішого. Розглянути також випадок, коли  Дж.
Дж.
12.6. Виразити через статистичний інтеграл  : термічне та калоричне рівняння стану, ентальпію
: термічне та калоричне рівняння стану, ентальпію 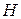 , потенціал Гіббса
, потенціал Гіббса 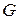 та хімічний потенціал
та хімічний потенціал 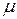 .
.
Розділ 13
СТАТИСТИЧНА ТЕОРІЯ КЛАСИЧНИХ
ІДЕАЛЬНИХ СИСТЕМ
Теоретичні відомості
Розподіли Максвелла – Больцмана, Больцмана, Максвелла. Система називається ідеальною, якщо її гамільтоніан  можна зобразити у вигляді
можна зобразити у вигляді
 , (13.1)
, (13.1)
де  – повна енергія і-ї частинки. До ідеальних систем відносяться ідеальний газ, випромінювання, тверде тіло (у гармонічному наближенні).
– повна енергія і-ї частинки. До ідеальних систем відносяться ідеальний газ, випромінювання, тверде тіло (у гармонічному наближенні).
Розглянемо найпростішу з таких систем – ідеальний газ у відсутності зовнішнього силового поля. Конфігураційний інтеграл QN у цьому випадку легко розраховується, оскільки  , якщо
, якщо  та
та  , якщо
, якщо  . При цьому зразу одержуємо
. При цьому зразу одержуємо
 . (13.2)
. (13.2)
Тоді з (12.27) статистичний інтеграл Z матиме вигляд
 (13.3)
(13.3)
або з урахуванням формули Стірлінга 
 . (13.4)
. (13.4)
Степеневий вигляд (13.4) дозволяє ввести статистичний інтеграл  , який припадає на одну частинку:
, який припадає на одну частинку:
 , (13.5)
, (13.5)
де n – число частинок в одиниці об’єму.
Розглянемо тепер ідеальний газ у деякому зовнішньому полі  ; тут
; тут  – набор трьох координат і-ї частинки. Тоді з канонічного розподілу (12.16) матимемо фазову щільність
– набор трьох координат і-ї частинки. Тоді з канонічного розподілу (12.16) матимемо фазову щільність  однієї (умовно першої) частинки:
однієї (умовно першої) частинки:
 (13.6)
(13.6)
або детальніше у декартових координатах
 , (13.7)
, (13.7)
де  . З (13.7) можна також одержати концентрацію
. З (13.7) можна також одержати концентрацію  частинок – середню їх кількість в одиниці об’єму. Розподіл (13.6) чи (13.7) називається розподілом Максвелла-Больцмана.
частинок – середню їх кількість в одиниці об’єму. Розподіл (13.6) чи (13.7) називається розподілом Максвелла-Больцмана.
Якщо проінтегрувати  за імпульсами
за імпульсами  , матимемо розподіл за координатами концентрації частинок ідеального газу у зовнішньому полі:
, матимемо розподіл за координатами концентрації частинок ідеального газу у зовнішньому полі:
 , (13.8)
, (13.8)
де  – концентрація частинок у точках, в яких
– концентрація частинок у точках, в яких  . Цей розподіл називається розподілом Больцмана.
. Цей розподіл називається розподілом Больцмана.
Проінтегрувавши (13.7) за координатами  , одержимо розподіл Максвелла за компонентами імпульсу
, одержимо розподіл Максвелла за компонентами імпульсу
 , (13.9)
, (13.9)
який легко перетворити й у розподіл за компонентами швидкості vх , vу , vz :
 . (13.10)
. (13.10)
Теорема про рівнорозподіл кінетичної енергії за ступенями вільності. Теорема про віріал.Визначення середніх значень за фазовою щільністю  , як вже зазначалося, зводиться до розрахунку
, як вже зазначалося, зводиться до розрахунку  , що в загальному випадку є досить складною задачею. Однак внутрішню енергію
, що в загальному випадку є досить складною задачею. Однак внутрішню енергію  (зокрема її кінетичну частину) можна вирахувати минаючи обчислення конфігураційного інтеграла. Покажемо це. Отже, позначимо через
(зокрема її кінетичну частину) можна вирахувати минаючи обчислення конфігураційного інтеграла. Покажемо це. Отже, позначимо через  кінетичну енергію, яка припадає на і-тий ступінь вільності системи. Величину
кінетичну енергію, яка припадає на і-тий ступінь вільності системи. Величину  можна записати, використовуючи гамільтоніан Н усієї системи:
можна записати, використовуючи гамільтоніан Н усієї системи:  . Знайдемо середнє значення
. Знайдемо середнє значення  за канонічним розподілом Гіббса. Матимемо
за канонічним розподілом Гіббса. Матимемо
 . (13.11)
. (13.11)
Зобразимо багатовимірний інтеграл в (13.11) у вигляді
 (13.12)
(13.12)
і обчислимо останній з них інтегруванням частинами, поклавши  ,
,  . Одержимо
. Одержимо

 . (13.13)
. (13.13)
Повертаючи результат (13.13) у (13.12), отримаємо
 . (13.14)
. (13.14)
Цей загальний результат класичної статистичної фізики називають теоремою про рівнорозподіл кінетичної енергії за ступенями вільності. Повна кінетична енергія  матиме вигляд
матиме вигляд
 , (13.15)
, (13.15)
де ν – число ступенів вільності системи. Зазначимо, що кількість ν не обмежується лише поступальними ступенями вільності.
Аналогічний розрахунок можна провести з величиною
 ,
,
яка називається віріалом, що припадає на і-тий ступінь вльності. Однак для одержання рівності  необхідно накласти обмеження на потенціальну енергію
необхідно накласти обмеження на потенціальну енергію  :
:  при
при  (чому?). Отже, результат
(чому?). Отже, результат
 (13.16)
(13.16)
у класичній статистичній фізиці називають теоремою про віріал.
Якщо потенціальна енергія  є однорідною функцією усіх своїх координат
є однорідною функцією усіх своїх координат  , користуючись (13.16), можна легко визначити кількісне значення
, користуючись (13.16), можна легко визначити кількісне значення  величини
величини  . Дійсно, за теоремою Ейлера для однорідних функцій маємо
. Дійсно, за теоремою Ейлера для однорідних функцій маємо
 , (13.17)
, (13.17)
де  – степінь однорідності функції
– степінь однорідності функції  . Це зразу дозволяє отримати
. Це зразу дозволяє отримати
 . (13.18)
. (13.18)
Тоді для повної енергії
 . (13.19)
. (13.19)
Наведені дві теореми часто використовуються для обчислень теплоємності систем.
