Дослід Резерфорда з розсіювання a-частинок
18.1 Мета роботи
Вивчити будову атома, впевнитись у справедливості теорії, яка базується на кулонівській взаємодії між  -частинкою та ядром атома.
-частинкою та ядром атома.
18.2 Вказівки з організації самостійної роботи
Розподіл позитивних і негативних зарядів в атомі можна з’ясувати шляхом безпосереднього “зондування” внутрішніх областей атома. Такий експеримент здійснив Резерфорд за допомогою  -частинок, спостерігаючи за напрямком їхнього руху під час проходження крізь тонкий шар речовини [3, 6].
-частинок, спостерігаючи за напрямком їхнього руху під час проходження крізь тонкий шар речовини [3, 6].
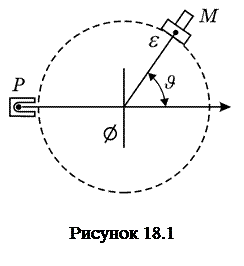
Дослід був здійснений таким чином. Вузький пучок  -частинок, які випромінювались радіоактивною речовиною Р (рис.18.1), падає на тонку металічну фольгу
-частинок, які випромінювались радіоактивною речовиною Р (рис.18.1), падає на тонку металічну фольгу  . Розсіяні
. Розсіяні  -частинки спричиняли сцинтиляції, які спостерігались у мікроскоп М. Екран і мікроскоп можна було встановлювати під будь-яким кутом
-частинки спричиняли сцинтиляції, які спостерігались у мікроскоп М. Екран і мікроскоп можна було встановлювати під будь-яким кутом  . Весь пристрій знаходився у вакуумі.
. Весь пристрій знаходився у вакуумі.
 Шар речовини фольги був настільки тонкий, що кожна
Шар речовини фольги був настільки тонкий, що кожна  -частинка під час проходження крізь нього пролітала поблизу тільки одного ядра і зазнавала лише одного розсіювання.
-частинка під час проходження крізь нього пролітала поблизу тільки одного ядра і зазнавала лише одного розсіювання.
Відхилення  -частинок обумовлені дією на них тільки з боку ядра. Помітного відхилення через взаємодію з електронами бути не може, оскільки маса електрона на чотири порядки менше маси
-частинок обумовлені дією на них тільки з боку ядра. Помітного відхилення через взаємодію з електронами бути не може, оскільки маса електрона на чотири порядки менше маси  -частинки. Коли частинка пролітає поблизу ядра, на неї діє кулонівська сила відштовхування
-частинки. Коли частинка пролітає поблизу ядра, на неї діє кулонівська сила відштовхування
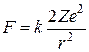 ,
,
де 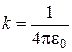 ,
, 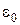 – електрична стала, е – заряд електрона, Z – порядковий номер елемента в таблиці Менделєєва, r – відстань між
– електрична стала, е – заряд електрона, Z – порядковий номер елемента в таблиці Менделєєва, r – відстань між  -частинкою та ядром. Відстань від ядра до вихідного напрямку польоту
-частинкою та ядром. Відстань від ядра до вихідного напрямку польоту  -частинки b називається прицільним параметром. Чим ближче від ядра пролітає частинка, тим сильніше вона повинна відхилятися.
-частинки b називається прицільним параметром. Чим ближче від ядра пролітає частинка, тим сильніше вона повинна відхилятися.
В результаті дослідів виявилось, що на великі кути (близькі до 180º) розсіювалася дуже мала кількість частинок. Аналізуючи результати, Резерфорд дійшов висновку, що сильне розсіювання частинок можливе тільки тоді, якщо всередині атома існує надзвичайно сильне електричне поле, яке створюється зарядом, пов’язаним з великою масою та сконцентроване в малому об’ємі. Базуючись на цьому висновку, Резерфорд запропонував у 1911 р. ядерну модель атома. Згідно з Резерфордом атом є системою зарядів, у центрі якої розташоване важке позитивне ядро з зарядом Zе, розміри якого не перевищують 10-14 м, а навколо нього розташовані Z електронів.
Виходячи з таких положень, Резерфорд розробив кількісну теорію розсіювання  -частинок, згідно з якою відхилення
-частинок, згідно з якою відхилення  -частинок обумовлені дією на них з боку атомного ядра. Помітного відхилення внаслідок взаємодії з електронами бути не може, оскільки маса електрона на чотири порядки менше маси
-частинок обумовлені дією на них з боку атомного ядра. Помітного відхилення внаслідок взаємодії з електронами бути не може, оскільки маса електрона на чотири порядки менше маси  -частинки. Коли частинка пролітає поблизу ядра, на неї діє кулонівська сила відштовхування
-частинки. Коли частинка пролітає поблизу ядра, на неї діє кулонівська сила відштовхування
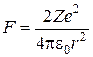 . (18.1)
. (18.1)
Сила (18.1) залежить від відстані як 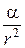 , (якщо позначити
, (якщо позначити 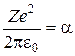 ) і є центральною силою.
) і є центральною силою.
Якщо 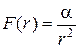 , де
, де 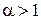 , то це відштовхуюча сила. У випадку відштовхування траєкторією частинки є гіпербола, а кут
, то це відштовхуюча сила. У випадку відштовхування траєкторією частинки є гіпербола, а кут 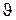 являє собою кут між асимптотами гіперболи.
являє собою кут між асимптотами гіперболи.
За формулою, яку отримав Резерфорд, можна обчислити відносну кількість частинок 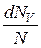 від загальної кількості
від загальної кількості 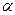 -частинок N, які розсіюються на ядрі в межах кута від
-частинок N, які розсіюються на ядрі в межах кута від 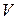 до
до 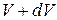 (рис.18.1).
(рис.18.1).
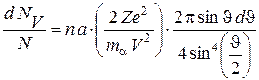 , (18.2)
, (18.2)
де n – кількість атомів в одиниці об’єму, a – товщина фольги. Ця формула відома як формула Резерфорда для розсіювання  -частинок.
-частинок.
Для даної речовини певної товщини фольги формулу можна записати у вигляді
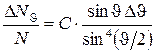 , (18.3)
, (18.3)
де 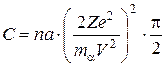 ;
; 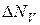 – кількість частинок, які розсіюються в межах кутів від
– кількість частинок, які розсіюються в межах кутів від 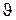 до
до 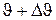 .
.
Справедливість теорії, яка походить із кулонівської взаємодії між
 -частинкою та ядром атома, свідчить про те, що навіть та частинка, яка відкидається в зворотному напрямку не проникає в середину ядра атома.
-частинкою та ядром атома, свідчить про те, що навіть та частинка, яка відкидається в зворотному напрямку не проникає в середину ядра атома.
 -частинка, що точно летить в напрямку до ядра, підійшла б до його центра на відстань, яку можна визначити, прирівнюючи кінетичну енергію
-частинка, що точно летить в напрямку до ядра, підійшла б до його центра на відстань, яку можна визначити, прирівнюючи кінетичну енергію  -частинки потенціальній енергії взаємодії
-частинки потенціальній енергії взаємодії  -частинки з ядром в момент повної зупинки частинки
-частинки з ядром в момент повної зупинки частинки
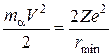 ,
,
де 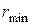 – мінімальна відстань між центрами
– мінімальна відстань між центрами  -частинки та ядра
-частинки та ядра
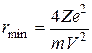 . (18.4)
. (18.4)
18.3 Опис комп’ютерної програми
Інтерфейс програми зображено на рис. 18.2. Програма базується на модифікованому алгоритмі Ейлера (див. додаток Б) та дозволяє розраховувати траєкторії руху  -частинок. Відповідні параметри дорівнюють:
-частинок. Відповідні параметри дорівнюють: 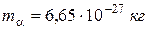 ,
, 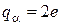 , де
, де 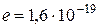 Кл. Вважаємо, що ядро (
Кл. Вважаємо, що ядро ( 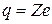 ) нерухоме. Внаслідок того, що характерна відстань взаємодії є приблизно 10-15 м, для сили, вираженої в ньютонах, виходитимуть дуже великі числа, які не придатні для комп’ютера. Відстані вимірюватимемо в фермі (1Ф=10-15 м) [10], а швидкості в одиницях швидкості світла
) нерухоме. Внаслідок того, що характерна відстань взаємодії є приблизно 10-15 м, для сили, вираженої в ньютонах, виходитимуть дуже великі числа, які не придатні для комп’ютера. Відстані вимірюватимемо в фермі (1Ф=10-15 м) [10], а швидкості в одиницях швидкості світла 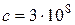 м/с.
м/с.
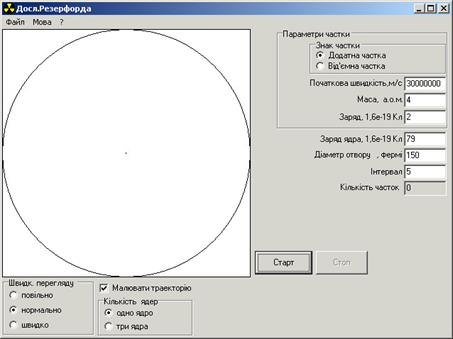
Рисунок 18.2
Програма дозволяє розраховувати і спостерігати на екрані траєкторію
 - частинки в полі нерухомого ядра з величиною заряду
- частинки в полі нерухомого ядра з величиною заряду 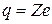 . Величина кута
. Величина кута 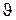 , під яким розсіюється
, під яким розсіюється  -частинка, залежить від її швидкості та прицільного параметра b. Під час натискування на старт
-частинка, залежить від її швидкості та прицільного параметра b. Під час натискування на старт  -частинки починають одна за одною вилітати з джерела, розташованого в лівій частині кола. Для того, щоб обмежитися спостереженням однієї частинки, треба після натискування на кнопку “Cтарт”, натиснути відразу кнопку “Cтоп”, при цьому у вікні “Количество частиц” з’являється цифра один. Можна спостерігати взагалі будь-яку кількість частинок, вони вилітатимуть доки не буде натиснута кнопка “Стоп”. На панель виведені вікна для введення заряду ядра Z ( в одиницях заряду електрона) початкової швидкості частинки. Причому швидкість в одиницях швидкості світла всіх частинок – однакова. Прицільний параметр
-частинки починають одна за одною вилітати з джерела, розташованого в лівій частині кола. Для того, щоб обмежитися спостереженням однієї частинки, треба після натискування на кнопку “Cтарт”, натиснути відразу кнопку “Cтоп”, при цьому у вікні “Количество частиц” з’являється цифра один. Можна спостерігати взагалі будь-яку кількість частинок, вони вилітатимуть доки не буде натиснута кнопка “Стоп”. На панель виведені вікна для введення заряду ядра Z ( в одиницях заряду електрона) початкової швидкості частинки. Причому швидкість в одиницях швидкості світла всіх частинок – однакова. Прицільний параметр 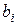 для кожної наступної частинки випадково змінюється в межах від b до –b.
для кожної наступної частинки випадково змінюється в межах від b до –b.
Програма також дає можливість побудувати діаграму розподілу кількості частинок 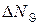 , кут відхилення яких попадає в проміжок кутів
, кут відхилення яких попадає в проміжок кутів 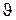 ,
, 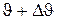 . Отримуючи розподіл
. Отримуючи розподіл 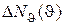 для різної кількості частинок N, можна переконатись, що розподіл, отриманий в комп’ютерному експерименті, буде тим ближчий до теоретичного (отриманого за формулою (18.2)), чим більша кількість частинок прийматиме участь в експерименті.
для різної кількості частинок N, можна переконатись, що розподіл, отриманий в комп’ютерному експерименті, буде тим ближчий до теоретичного (отриманого за формулою (18.2)), чим більша кількість частинок прийматиме участь в експерименті.
Програма дозволяє регулювати швидкість огляду руху частинки.
Щоб прискорити побудову діаграми при великій кількості частинок, можна взагалі не рисувати траєкторії руху.
18.4 Інструкція користувачу
1. Вибрати максимальне значення прицільного параметра (діаметр отвору) 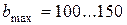 ф. Спостерігати траєкторію руху
ф. Спостерігати траєкторію руху  -частинок в залежності від значення b.
-частинок в залежності від значення b.
2. Створити умови для спостереження однієї – декількох  -частинок при параметрі
-частинок при параметрі 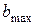 . Яку форму має траєкторія
. Яку форму має траєкторія  -частинки?
-частинки?
3. Задати “діаметр отвору” 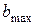 (тобто діаметр пучка
(тобто діаметр пучка  -частинок) і початкову швидкість згідно з табл. 18.1. Натиснути на кнопку “Старт” і спостерігати розсіювання
-частинок) і початкову швидкість згідно з табл. 18.1. Натиснути на кнопку “Старт” і спостерігати розсіювання 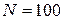 частинок.
частинок.
4. Зарисувати діаграму розсіювання частинок. Виконати розрахунок за формулою (18.2). Порівняти результати розрахунку з наведеними на діаграмі.
5. Повторити дослід пунктів 3, 4 для 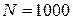 ,
, 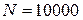 частинок. Зробити висновок.
частинок. Зробити висновок.
Таблиця 18.1 – Вихідні дані
| Номер вар. | 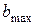 , ф , ф | Z | 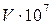 , м/c , м/c | Номер вар. | 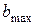 , ф , ф | Z | 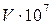 , м/c , м/c |
| 3,5 | |||||||
| 3,5 | |||||||
| 3,5 | |||||||
| 3,5 | |||||||
| 3,5 | |||||||
| 3,5 |
6. Результати виконання роботи занести до табл. 18.2. Таблиця складена для випадку, коли 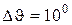 , підраховано відношення для цього випадку величини
, підраховано відношення для цього випадку величини 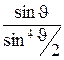 , змінної в формулі Резерфорда (18.3). У величині теоретичній
, змінної в формулі Резерфорда (18.3). У величині теоретичній 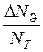
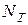 має підраховуватися як сума всіх значень
має підраховуватися як сума всіх значень 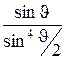 , наведених у відповідному стовпчику табл. 18.2, тобто
, наведених у відповідному стовпчику табл. 18.2, тобто 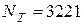 . В цьому випадку не має значення, яку величину матиме константа С у формулі (18.3).
. В цьому випадку не має значення, яку величину матиме константа С у формулі (18.3).
Таблиця 18.2 – Результати розрахунків
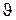 ,° ,° | 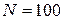 | 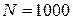 | 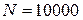 | |||||||||
| Експер. | Теорія | Експер. | Теорія | Експер. | Теорія | |||||||
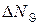 | 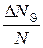 | 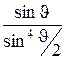 | 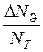 | 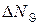 | 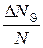 | 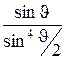 | 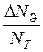 | 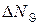 | 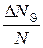 | 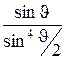 | 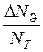 | |
| 9,4 | 9,4 | 9,4 | ||||||||||
| 5,8 | 5,8 | 5,8 | ||||||||||
| 2,8 | 2,8 | 2,8 |
Експериментальне значення 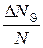 підраховується для відповідного значення
підраховується для відповідного значення 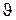 , як відношення висоти стовпчика на діаграмі
, як відношення висоти стовпчика на діаграмі 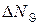 до повної кількість частинок, які приймають участь в експерименті.
до повної кількість частинок, які приймають участь в експерименті.
18.5 Зміст звіту
Звіт має містити: мету роботи, діаграму розсіювання частинок, результати вимірювань і розрахунків, зведені в таблиці, висновки на основі отриманих результатів та пунктів завдання 1...5.
18.6 Контрольні запитання і завдання
1. В чому ідея експерименту Резерфорда?
2. З чого складалась експериментальна установка Резерфорда?
3. Яку модель атома запропонував Резерфорд, базуючись на результатах дослідів?
4. На чому базувалася кількісна теорія розсіювання α-частинок?
5. Яку траєкторію мають описувати α-частинки в центральному полі кулонівської сили?
6. Що дає можливість обчислити формула Резерфорда?
7. Як описується рух α-частинки в полі ядра (яким алгоритмом)?
8. Що таке “прицільний параметр”?
9. В якому вигляді мають бути наведені результати модельного експерименту?
10. Як здійснюється порівняння теоретичних результатів (за формулою Резерфорда) та результатів модельного експерименту?
