Перше начало термодинаміки
Теоретичні відомості
Формулювання першого начала. Перше начало термодинаміки встановлює, що внутрішня енергія є однозначною функцією стану системи, а її зміна можлива лише під впливом зовнішніх факторів. У термодинаміці розрізняють два типи зовнішніх впливів за їх дією на зовнішні параметри системи. Це впливи, які призводять до зміни зовнішніх параметрів, що супроводжується здійсненням роботи 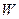 системою. А також впливи, не пов’язані зі зміною зовнішніх параметрів, але які супроводжуються передачею деякої кількості теплоти
системою. А також впливи, не пов’язані зі зміною зовнішніх параметрів, але які супроводжуються передачею деякої кількості теплоти 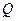 системі.
системі.
Отже, на підставі закону збереження енергії зміна внутрішньої енергії  системи при її переході зі стану 1 в стан 2 дорівнюватиме алгебраїчній сумі
системи при її переході зі стану 1 в стан 2 дорівнюватиме алгебраїчній сумі 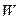 та
та  . Через домовленість (див. розділ 0) про знаки величин
. Через домовленість (див. розділ 0) про знаки величин 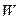 та
та  і з урахуванням того, що додатна робота призводить до зменшення внутрішньої енергії, математичний запис цього твердження буде таким:
і з урахуванням того, що додатна робота призводить до зменшення внутрішньої енергії, математичний запис цього твердження буде таким:

або
 (2.1)
(2.1)
Для елементарного процесу  співвідношення (2.1) набирає вигляду
співвідношення (2.1) набирає вигляду
 (2.2)
(2.2)
Формули (2.1) та (2.2) є математичними виразами першого начала термодинаміки.
Через те, що внутрішня енергія  є однозначною функцією стану системи,
є однозначною функцією стану системи,  буде повним диференціалом змінних
буде повним диференціалом змінних  . При цьому різниця
. При цьому різниця  залежить лише від станів 2 і 1, але не залежить від шляху переходу системи зі стану 1 в стан 2. В той же час величини
залежить лише від станів 2 і 1, але не залежить від шляху переходу системи зі стану 1 в стан 2. В той же час величини  і
і 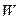 в загальному випадку є функціями шляху, тобто функціоналами.
в загальному випадку є функціями шляху, тобто функціоналами.
Для кругових процесів (циклів) через те, що  , рівність (2.1) дає
, рівність (2.1) дає
 , (2.3)
, (2.3)
тобто робота в цьому випадку здійснюється лише за рахунок отримання системою теплоти від зовнішніх тіл. Тому перше начало термодинаміки часто формулюють у вигляді положення про неможливість вічного двигуна першого роду, тобто такого періодично діючого пристрою, який би здійснював роботу не забираючи енергію зовні. Докладніше (2.2) можна записати у вигляді

або, оскільки 
 (2.4)
(2.4)
Отже, згідно з (2.4) dQ являє собою диференціальну форму (форму Пфаффа) змінних  . Підкреслимо, що в загальному випадку
. Підкреслимо, що в загальному випадку  .
.
Теплоємність. Властивості термодинамічних систем підрозділяють на термічні і калоричні. Ті з них, які визначаються лише термічними рівняннями стану, називаються термічними властивостями. Ті властивості, для визначення яких необхідно знати ще й калоричне рівняння стану системи, називаються калоричними. Важливою калоричною властивістю є теплоємність  системи. Вона визначається як кількість теплоти, що необхідна для зміни температури системи на 1К, тобто
системи. Вона визначається як кількість теплоти, що необхідна для зміни температури системи на 1К, тобто
 . (2.5)
. (2.5)
З (2.4) видно, що  визначається парою нескінечнно близьких станів у просторі
визначається парою нескінечнно близьких станів у просторі  змінних. Звідси випливає, що теплоємність С залежить від умов, за яких визначається
змінних. Звідси випливає, що теплоємність С залежить від умов, за яких визначається  . Це означає, що вона є не функцією стану, а саме функцією процесу: одна й та ж система має різні значення
. Це означає, що вона є не функцією стану, а саме функцією процесу: одна й та ж система має різні значення 
Визначення теплоємності призводить до такого важливого поняття в термодинаміці, як термостат. Термостат - це таке тіло, у якого  . Коли говорять про систему, поміщену в термостат, мають на увазі, що за будь-яких процесів у ній температура підтримується постійною.
. Коли говорять про систему, поміщену в термостат, мають на увазі, що за будь-яких процесів у ній температура підтримується постійною.
Перше начало термодинаміки дозволяє визначити значення всіх теплоємностей, а також встановити зв’язок між ними, якщо відомі термічні і калоричне рівняння стану. Так, наприклад, для простої системи, коли задані рівняння стану

 , (2.6)
, (2.6)
з (2.4) знайдемо
 (2.7)
(2.7)
Звідси бачимо, що для процесу, коли  ,
,
 (2.8)
(2.8)
Якщо  , то
, то
 (2.9)
(2.9)
і
 . (2.10)
. (2.10)
Основні термодинамічні процеси. В будь-якій термодинамічній системі можливі два процеси: ізотермічний  і політропний
і політропний  ; адіабатний процес
; адіабатний процес  - окремий випадок політропного. Для конкретних систем можливі й інші процеси, які залежать від природи системи. Так, наприклад, для простої системи з зовнішнім параметром
- окремий випадок політропного. Для конкретних систем можливі й інші процеси, які залежать від природи системи. Так, наприклад, для простої системи з зовнішнім параметром 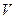 існує ще ізохорний процес
існує ще ізохорний процес  і ізобарний процес
і ізобарний процес  . Названі п’ять процесів виявляються найбільш важливими в термодинаміці. Функціональний зв’язок між парою з величин
. Названі п’ять процесів виявляються найбільш важливими в термодинаміці. Функціональний зв’язок між парою з величин  при відповідному процесі називається рівнянням цього процесу. Рівняння ізотермічного, ізохорного й ізобарного процесів можна отримати одразу з термічного рівняння стану даної системи. Зокрема, для ідеального газу рівняння цих процесів містяться в формулі Менделєєва-Клапейрона (0.12). Для знаходження рівняння політропного процесу необхідне як знання рівнянь стану конкретної системи, так і використання першого начала термодинаміки.
при відповідному процесі називається рівнянням цього процесу. Рівняння ізотермічного, ізохорного й ізобарного процесів можна отримати одразу з термічного рівняння стану даної системи. Зокрема, для ідеального газу рівняння цих процесів містяться в формулі Менделєєва-Клапейрона (0.12). Для знаходження рівняння політропного процесу необхідне як знання рівнянь стану конкретної системи, так і використання першого начала термодинаміки.
Співвідношення (2.7), що випливає з першого начала, вже можна розглядати як диференціальне рівняння (в змінних  ) політропи для простої системи з зовнішнім параметром
) політропи для простої системи з зовнішнім параметром  і відповідною йому узагальненою силою
і відповідною йому узагальненою силою  . Як бачимо, для його інтегрування необхідно мати і термічне, і калоричне рівняння стану. Це диференціальне рівняння можна записати також через теплоємності
. Як бачимо, для його інтегрування необхідно мати і термічне, і калоричне рівняння стану. Це диференціальне рівняння можна записати також через теплоємності  і
і  . Для цього перенесемо вліво перший доданок
. Для цього перенесемо вліво перший доданок  правої частини (2.7) і отриману рівність розділимо на рівняння (2.10). В результаті з урахуванням
правої частини (2.7) і отриману рівність розділимо на рівняння (2.10). В результаті з урахуванням  одержимо
одержимо
 (2.11)
(2.11)
Інтегрування (2.11) після попередніх вирахування  і підстановки
і підстановки  , як функцій
, як функцій  і
і 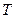 , дасть рівняння політропи в змінних
, дасть рівняння політропи в змінних  Якщо зручніше працювати в змінних
Якщо зручніше працювати в змінних  або
або  то можна скористатися формулами
то можна скористатися формулами

або

відповідно, за допомогою яких виключається “зайвий” диференціал в (2.7) або (2.11). Для адіабатичного процесу  рівняння (2.11) набирає вигляду
рівняння (2.11) набирає вигляду
 (2.12)
(2.12)
де  - так званий показник адіабати. Якщо
- так званий показник адіабати. Якщо  , то
, то  і (2.12) можна переписати як
і (2.12) можна переписати як
 (2.13)
(2.13)
де тепер  .
.
