Моделирование суммы двух и более равномерно распределенных случайных величин
Рассмотрим распределение суммы двух случайных величин, имеющих прямоугольное распределение на примере игры «Крепс».Смысл игры состоит в подбрасывании двух игральных костей, вычислении суммы выпавших очков и определении условий игры.
Очевидно, что для одной кости выпадение каждой из шести граней (и, таким образом, цифр 1, 2, 3, 4, 5 и 6) игральной кости является событием равновероятным и равным 1/6. Такой же вывод можно сделать и для второй игральной кости. Для удобства анализа сделаем кости различными, окрасив их, скажем, в красный и зеленый цвета. Тогда подбрасывание двух костей имеет 6*6=36 равновероятных исходов, которые приведены ниже в таблице 1.
Таблица 1
| Зеленая кость | |||||||
| К | |||||||
| р | |||||||
| а | |||||||
| с | |||||||
| н | |||||||
| а | |||||||
| я |
В выделенных клетках таблицы 1 указана соответствующая сумма очков. Рассчитаем распределение вероятности P суммы очков при одновременном подбрасывании двух костей. В таблице 2 представлены результаты такого расчета.
Таблица 2
| Сумма, С | |||||||||||
| Вероятность, Р | 1/36 | 2/36 | 3/36 | 4/36 | 5/36 | 6/36 | 5/36 | 4/36 | 3/36 | 2/36 | 1/36 |
Проанализируем график зависимости вероятности суммы очков Р от величины этой суммы. На рисунке 3 представлена эта зависимость.
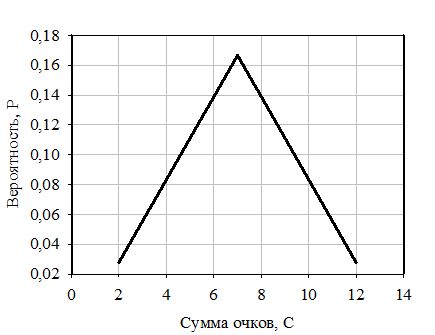 |
| Рисунок 3 - Зависимость вероятности суммы очков, от величины суммы очков |
Из рисунка 3 видно, что вероятность Р суммы очков игральных костей описывается треугольным распределением. Таким образом, при суммировании двух случайных событий, имеющих равномерное распределение, получается распределение близкое к треугольному.
При рассмотрении суммы m случайных величин, имеющих прямоугольное распределение, обнаруживается, что при повышении значения m (m=6 и более), получаемое распределение стремится к нормальному распределению, т.е. к распределению, описываемому законом Гаусса.
Моделирование Распределения Максвелла
Распределение Максвелла для скоростей газовых молекул доказано из предположения о распределении проекции скоростей молекул по нормальному закону (1). При этом случайная величина η абсолютного значения скорости записывается через компоненты скорости как
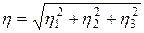 . (4)
. (4)
В настоящей работе для трех случайных величин ηi (m = 6) строится гистограмма и сравнивается с функцией распределения (3).
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Запустите программу ModelMax, ярлык программы находится на рабочем столе.
На экране монитора ЭВМ возникнет открывающееся меню «Модель распределения Максвелла», в котором появятся окошки выбора условий проведения модельного эксперимента:
· Окошко выбора температуры в кельвинах (К) и интервал изменения температур (1-900);
· Окошко выбора массы молекул газа (а.е.м.) и интервал изменения а.е.м. (1-100);
· Окошко значения постоянной Больцмана (Дж/К);
· Окошко со значением числа молекул и интервал числа молекул при проведении модельного эксперимента (5-2500);
· Кнопка «Старт», предназначенная для запуска программы моделирования распределения Максвелла при заданных условиях модельного эксперимента;
· Кнопка «Выход» для выхода из программы и окончания работы.
2. Внимательно изучите меню перед началом работы. Клавиша <F1> вызывает встроенную справку. В окошках уже имеются значения, принимаемые по умолчанию. Вам их надо заменить. О том, как это делается, прочтите во встроенной справке.
3. Установите газ - водород, температуру - 273 К, число молекул - 500.
4. Для запуска модели щелкните мышью по кнопке «Старт» или нажмите клавишу <Enter> . На экране монитора появится окно, в котором будут :
· Окошко с изображением графической информации (гистограммы и функции распределения Максвелла), над которым изображен ползунок для задания температуры и изменения ее в процессе проведения эксперимента;
· Окошко для наблюдения за характером движения молекул рассматриваемой модели термодинамической системы. Учтите, что динамическая модель движения молекул строится в плоскости XY без учета составляющей Z и не в реальном масштабе времени и скоростей молекул (определите почему );
· Значения рассчитанных наиболее вероятной, средней и среднеквадратичной скоростей молекул при заданных температурах (нижняя часть окна).
5. Для получения более подробной справки об окне моделирования нажмите клавишу <F1>.
6. Проведите модельный эксперимент для различных газов (водорода, гелия, азота, кислорода, радона и др.) при различных температурах и различном числе молекул (по заданию преподавателя). Проанализируйте характер изменения гистограмм, вид теоретической кривой распределения молекул по скоростям при изменении температуры, числа молекул и вида газа. Результаты расчета скоростей для различных газов при различных температурах запишите в таблицу 3.
7. Изобразите графики функции распределения Максвелла для одного из исследуемых газов при различных температурах и числе молекул, равном 2500.
8. Сделайте краткие выводы по работе.
Таблица 3
| Газ | Температура, К | Наиболее вероятная скорость, Vв, м/с | Средняя скорость, <V>, м/с | Среднеквадратичная скорость, Vкв, м/с |
| Водород | ||||
| Гелий | ||||
| Азот | ||||
| Кислород | ||||
| Радон | ||||
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Запишите функцию распределения молекул (распределение Максвелла) по скоростям для идеального газа.
2. Определите среднюю, наиболее вероятную и среднеквадратическую скорости.
3. Поясните физический смысл функции распределения.
4. Определите по графику относительное число молекул, скорости которых больше или меньше определенной скорости.
5. Рассчитайте относительное число молекул, скорости которых находятся в интервале скоростей от 0 до ∞.
6. Объясните методику исследования распределения молекул по скоростям. Поясните моделирование равномерного, треугольного и гауссова распределения. Докажите на примере игры «Крепс» переход от равномерного к треугольному распределению случайных событий.
