Детекторы ионизирующих излучений

Лабораторная работа № 1

Изучение счетчика Гейгера-Мюллера

Цель работы: изучение методов регистрации ядерных излучений.

Оборудование: работа выполняется на любой установке практикума по ядерной физике.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.

Работа с соответствующей установкой описана в приложении «радиометрические приборы».

Задание

1. Изучить зависимость скорости счета N от напряжения V.

2. Измерение каждой точки кривой N=f(V) производить с относительной ошибкой 3÷4%.

3. Построить график зависимости N=f(V).

4. Указать рабочую точку, протяженности «плато» (в вольтах), а также его наклон (в процентах на 100в).

5. На рабочей точке рассчитать истинное количество частиц попавших в счетчик с учетом мертвого времени, исходя из τ=10^-4 сек.

6. Измерить фон.

КОНТРОЛЬНЫЕ ВОПРОСЫ.

1. Схема установки и назначение приборов.

2. Достоинства и недостатки детекторов данного типа.

3. Каковы основные характеристики счетчиков числа частиц?

4. В чем отличие счетчиков Гейгера-Мюллера от других счетчиков

5. Что называют счетной характеристикой счетчика Г.-М.?

6. Каковы механизмы регистрации заряженных и незаряженных частиц

счетчиками Гейгера-Мюллера?

ПРИЛОЖЕНИЕ.

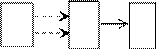
Ионизирующим излучением (ИИ) называют излучение, взаимодейст- вие которого со средой приводит к образованию ионов разных знаков (свет и ультрафиолетовое излучение не включают в это понятие) [1].Регистрация ИИ заключается в обнаружении и определении вида частиц, измерении пото- ка и спектра излучения; регистрация ИИ происходит в результате его взаи- модействия с веществом. Взаимодействие сопровождается несколькими эф- фектами: ионизацией, испусканием ионизированными и возбужденными атомами и молекулами фотонов, выделением тепла. В зависимости от эффек- та взаимодействия методы регистрации ИИ подразделяют на: ионизацион- ные, сцинтилляционные, калориметрические и т.д., однако структурная схе- ма эксперимента во всех случаях одинакова (рис. 1) [2,3].

1 2 2 5

3 4 6 7

Рис.1. Схема эксперимента по регистрации ионизирующего излучения

Излучение 2 от источника ИИ 1 после прохождения селектора 3 попа- дает в объем детектора 4. Взаимодействуя с веществом детектора, излучение теряет в нем часть или всю энергию. В результате поглощения энергии излу- чения в объеме детектора его состояние изменяется, что приводит к появле- нию сигнала 5, который усиливается, анализируется и регистрируется в уст- ройствах 6 и 7.

Детекторы ионизирующих излучений

Детектор – прибор для регистрации и измерения характеристик час-

тиц ионизирующих излучений.

Существуют различные типы детекторов как преобразователей энергии

регистрируемых излучений в сигналы.

1. Счетчики частиц, которыми могут быть любые детекторы, регист-

рирующие отдельные частицы (независимо от природы сигнала) и работаю-

щие со схемами, регистрирующими только число импульсов. При этом необ- ходимо, чтобы одной попавшей в объем детектора частице соответствовал один сигнал. Счетчики могут быть газонаполненными (ионизационные каме- ры, пропорциональные, Гейгера-Мюллера, искровые), оптическими (сцин- тилляционные, черенковские) и твердотельными (кристаллические, полупро- водниковые).

2. Пропорциональные детекторы, в которых сигнал пропорционален поглощенной в их объеме энергии. В качестве сигнала могут быть амплитуда

электрического импульса, длина трека частиц, число проявленных зерен вдоль трека и т.д. Любой пропорциональный детектор можно использовать и

в качестве счетчика частиц. Причем схема регистрации считает импульсы с амплитудой, большей определенной величины (порога срабатывания измери- тельной аппаратуры).

3. Трековые детекторы позволяют наблюдать визуально или фиксиро- вать фотографически или электромагнитными методами треки частиц в сре- де, через которую они проходят. Информацию об излучении несут в себе

геометрия треков (число треков и направление движения заряженных час- тиц), толщина трека (величина энергетических потерь на единицу длины, скорость и заряд частицы) и длина трека (энергия частицы). К трековым де- текторам относятся: камеры Вильсона, диффузионные и пузырьковые, ядер-

ные фотоэмульсии, твердотельные трековые детекторы и т.д.

Характеристики счетчиков

Сравнительные характеристики некоторых детекторов, используемых в счетчиках частиц [2], представлены в табл. 1.

Таблица 1

Характеристики детекторов, используемых в счетчиках частиц

Детектор	Эффективность регистрации излучения h,%	Разрешающее время t, c
Альфа	Бэта	Гамма
Пропорциональный Гейгера - Мюллера Сцинтилляционный Полупроводниковый			мало   <1   <30   <10	10-6 -10-8   10-3 -10-5   10-7 -10-9   10-7

Пространственное разрешение указанных детекторов около 1см.

1. Эффективность регистрации определяется из соотношения

h= N p ×100%,

N

(1)

где N p

– число зарегистрированных частиц за время измерений; N – число

частиц, попавших за то же время в рабочий объем детектора через входное окно или боковые стенки. Эффективность регистрации различна для различ- ных счетчиков и зависит от вида и энергии излучения, типа и размеров де- тектора, режима питания детектора и уровня (порога) чувствительности из- мерительного прибора, на вход которого поступает сигнал с детектора (уси- лителя).

2. Спектральная характеристика – зависимость эффективности реги-

страции частиц (квантов) от энергии частицы (кванта) при прочих равных условиях; она связана с состоянием рабочего вещества и толщиной входного

окна детектора.

3. Разрешающее время t характеризует наименьший промежуток вре-

мени между попаданиями двух частиц, при котором будут зарегистрированы обе частицы отдельно; зависит от длительности процессов, происходящих после попадания частицы в рабочий объём детектора и быстродействия из- мерительного прибора.

4. Счетная характеристика – зависимость скорости счета, т.е. числа зарегистрированных в единицу времени импульсов, от напряжения U между электродами счетчика при неизменном числе частиц, попадающих в рабочий

объем счетчика в единицу времени. Счетная характеристика имеет, как пра- вило, плато, т.е. участок, где скорость счета практически не зависит от на- пряжения между электродами.

Счетчики Гейгера-Мюллера

Счетчик Гейгера-Мюллера (Г.-М.) – детектор частиц ионизирующих излучений, действие которого основано на возникновении самостоятельного разряда в газе при попадании частиц в его объем. При напряжениях на элек- тродах, меньших напряжения пробоя, заполняющий счетчик газ сам по себе не проводит электрический ток. Проводимость газа связана с образованием пар ионов под действием ионизирующего излучения. Счетчики этого типа используют для регистрации как заряженных, так и незаряженных частиц. Регистрация незаряженных частиц осуществляется по вторичным заряжен- ным частицам (электронам и положительно заряженным ионам), возникаю- щим при взаимодействии незаряженных частиц с рабочим веществом и стен- ками детектора. При этом толщина стенок счетчика не должна превышать средней длины свободного пробега вторичных электронов. Счетчики Г.-М.

благодаря хорошей чувствительности к различным видам ионизирующих из- лучений, высокой надежности и простоте изготовления широко применяются в радиометрической технике.

Счетчики Г.-М. бывают двух ти-

пов: цилиндрические и торцовые. Ци- 1 -

линдрический счетчик (рис. 2) изготав- 2

ливают из тонкой металлической или +

металлизированной изнутри, стеклян-

ной, герметически замкнутой трубки 1 и

металлической нити 2, натянутой вдоль оси внешней оболочки. Нить служит анодом, трубка – катодом. У торцового

Рис.2. Схема цилиндрического счетчика Гейгера-Мюллера

счетчика (рис.3) металлизированный стеклянный корпус 1 является катодом,

нить 2 – анодом, а торец корпуса образует тонкое слюдяное окно 3 толщиной

20-30 мкм. Конец нити 2 для предотвращения коронного разряда на острие закрыт стеклянной бусинкой.

Ионизирующее излучение попадает в объем счетчика либо через боко- вую поверхность у цилиндрического, либо через слюдяное окно у торцового счетчика. Объем счетчиков заполняется благородными газами: аргоном или

неоном; рабочее напряжение, подаваемое на

счетчик, связано с давлением газа в объеме 2 1

счетчика (обычно оно составляет 100-200 мм 3

рт.ст.).

В лаборатории ядерной физики исполь- +

зуются цилиндрические счетчики типов СТС-

5, СТС-6, МС-9, торцовые счетчики типов -

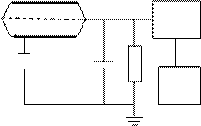
СБТ-7, СБТ-9, СБТ-11, СИ-2Б. Схема включе-

ния счетчиков приведена на рис. 4. Электроды счетчика Г.-М., находящиеся под напряжением U 0 , образуют газоразрядный промежуток с

Рис. 3. Схема торцового счетчика Гейгера-Мюллера

с . Г.-М.

сильно неоднородным электрическим полем. Ес-

ли напряжение превышает напряжение начала

У счета U HC

(U HC

может быть

300 ¸1500

В), то любая

Uo C R

ПУ

заряженная частица, попавшая в рабочий объем

счетчика и образовавшая хотя бы пару ионов,

вызовет в нем вспышку газового разряда за вре-

мя 10 -7 ¸10 -6 с. Возникающий при этом во внеш-

Рис. 4. Схема включения счетчика Гейгера-Мюллера

ней цепи импульс тока возрастает в усилителе У и регистрируется пересчетным устройством ПУ (рис.4).

Поскольку счетчики Г.-М. являются

газонаполненными детекторами, рассмотрим в целом вольтамперную

характеристику газового разряда (явление протекания ионизационного тока через газы), т.е. зависимость ионизационного тока или амплитуды импульса

DU от напряжения на электродах U при постоянной интенсивности

ионизирующего излучения в газе (рис. 5).

При напряжениях от 0 до U1

на электродах газоразрядного счетчика

амплитуда импульса (ионизационного тока) пропорциональна напряжению.

В этой области при U < U1

не все образовавшиеся под действием ионизирую-

щего излучения ионы достигают электродов, так как часть положительных ионов и электронов при столкновениях между собой рекомбинирует. С уве- личением напряжения растет скорость направленного движения электронов и ионов, вероятность рекомбинации уменьшается, что приводит к возрастанию тока.

На участке от U1

до U2

ионизационный ток практически постоянен, по-

скольку почти все ионы первичной ионизации собираются на электродах, а других источников зарядов в газе нет. Амплитуда тока пропорциональна

первичной ионизации no

(кривая 2 на рис. 5 соответствует частицам с боль-

шей первичной ионизацией). В этой области напряжений работают иониза-

ционные камеры.

DU

2

0 U1

U

U U U U

2 3 4 5

Рис.5. Вольтамперная характеристика газового разряда

На участке U > U 2

ионизационный ток возрастает с ростом U из-за вто-

ричной ионизации. В случае цилиндрического счетчика электрическое поле в нем крайне неоднородно и на расстоянии r от оси счетчика равно

E(r ) =

U ,

r ×ln(rk /ra )

(2)

где rk и r a

– радиусы катода и анода (нити) соответственно. Вблизи анода

( r » 10 -2 см) поле возрастает до такой степени, что электрон между двумя по- следовательными столкновениями приобретает кинетическую энергию, дос- таточную для ионизации атомов газа счетчика (ударная ионизация). Элек- троны вторичной ионизации вместе с электронами первичной ионизации в дальнейшем ионизируют другие атомы – происходит лавинное образование

зарядов. После попадания первой лавины (за время

»10-6 с) электронов на

анод разряд на этом не прекращается, так как при столкновении электронов с нейтральными атомами и молекулами газов происходит не только ионизация, но и возбуждение атомов, что приводит к испусканию фотонов. Фотоны об- разуются и при нейтрализации положительных ионов на катоде. Часть из об- разовавшихся в обоих случаях фотонов имеет энергию, превышающую рабо- ту выхода электронов из материала катода. Это приводит к образованию фо- тоэлектронов, которые начинают двигаться к аноду, вызывая вторичную и последующие лавины. Если начальное число пар ионов (число первичных

лавин), образованных одной частицей ионизирующего излучения, равно

no , а

каждая первичная лавина состоит в среднем из m пар ионов, то полное число

ионов во всех

no первичных лавинах будет

no × m

электронов. Если каждый из

электронов на своем пути к аноду создаст hвозбужденных атомов (молекул),

o

то будет испущено

n × m ×h

фотонов. Попав на катод счетчика, каждый из

фотонов с вероятностью

g»10-4

вырвет с его поверхности фотоэлектрон.

o

Эти

g × n

× m ×h

фотоэлектронов, двигаясь в электрическом поле от катода к

o

аноду, создадут серию вторичных лавин из личество ионных пар во всех лавинах

g × n

× m 2 ×h

электронов и т.д. Ко-

N = no

× m(1 + g ×h × m + (g ×h × m) 2 + K) =

¥

åno

k =1

(h × g ) k -1 m k .

(3)

Отношение ионизационного эффекта N к первоначальному числу пар ионов, образованных одной частицей ионизирующего излучения, называют коэффициентом газового усиления M :

M = N .

no

(4)

Если

g×h×m < 1 (область от U2

до U 3

на рис.5, когда число ионных пар

m в одной первичной лавине невелико), то в каждой последующей лавине образуется меньше пар ионов, чем в предыдущей, и газовый разряд затухает со временем. Коэффициент газового усиления в этом случае равен

а при g×h×m <1

M = m ,

1 -g×h×m

(5)

M = m,

т.е. газовое усиление обусловлено только ударной ионизацией. В области от

U2 до U 3

работают пропорциональные счетчики (величина импульса пропор-

циональна первичной ионизации), а коэффициент газового усиления M при

повышении напряжения изменяется от 1 до 102 -104. Область U < U

сит название области ограниченной пропорциональности.

< U 4

но-

При

U > U 4

на рис.5 величина

g ×h × m = 1

и разряд становится незату-

хающим (самостоятельным). Область напряжений от U4

до U 5

называется

областью Гейгера-Мюллера. Коэффициент газового усиления здесь достигает

1010 ,

а величина импульса напряжения DU

– нескольких вольт и даже десят-

ков вольт, причем DU

не зависит от первоначальной ионизации (кривые 1 и 2

на рис. 5 при

U 4 < U

< U 5

совпадают). Это связано с тем, что при увеличе-

нии напряжения на счетчике область ударной ионизации увеличивается, при-

водя к увеличению ионизации вследствие вторичных процессов (электрон-

ных и фотонных). При напряжениях

U > U 4 = U HC

коэффициент газового

усиления M ,

а соответственно и ток, протекающий через газоразрядный

промежуток, должны были бы неограниченно возрастать, так как

M ® ¥

при

g×h×m ®1

(см формулы 3,4). Однако в действительности из-за ограничения

тока пространственным зарядом (экранирование анода облаком положитель-

но заряженных ионов из-за их малой дрейфовой скорости при напряжениях

U > U 4 )

чение.

газовое усиление M имеет хотя и очень большое, но конечное зна-

При U > U5

происходит самопроизвольный пробой газа и разряд стано-

вится неуправляемым.

В области Гейгера-Мюллера

(U4 < U

< U 5 )

газовый разряд при посто-

янном напряжении на счетчике является незатухающим, но остается вынуж- денным, т.е. самопроизвольного разряда не происходит – нужна первона- чальная ионизация. Самостоятельный газовый разряд может быть использо- ван для регистрации ионизирующих излучений при условии, что он может быть быстро погашен. В противном случае разряды от двух последователь- ных во времени частиц, попавших в счетчик, могут наложиться друг на друга и две эти частицы будут сосчитаны как одна.

Если каким-либо образом разность потенциалов между электродами

счетчика понизить и сделать на 1-3

В меньше, чем напряжение начала счета

U HC ,

ток в счетчике станет неустойчивым и газовый разряд, благодаря слу-

чайным флуктуациям, оборвется. С этой целью в цепь счетчика (рис.4) вклю-

чают достаточно большое сопротивление

R(108 ¸ 1010

Ом), при котором значе-

ние тока в счетчике попадает в область неустойчивости. При выполнении данных условий вспышка газового разряда, вызванная попавшей в объем

счетчика ионизирующей частицей, спустя некоторое время (около прекращается.

10-4 с)

Высокоомное сопротивление R в цепи счетчика требуется еще и для того, чтобы замедлить возрастание напряжения между электродами и дать

время для удаления положительных ионов из рабочего объема. При этом ем-

кость счетчика C и дополнительное сопротивление должны быть такими,

чтобы постоянная времени схемы

T = RC

была порядка времени дрейфа по-

ложительных ионов к катоду. При

R = 108 ¸1010

Ом и

C = 20 пФ

T = (108 ¸1010 ) ×20 ×10-12 = (10-4 ¸10-2 ) с.

Гашения разряда в счетчике добиваются также, добавляя к основному наполнителю другую смесь газов. Это могут быть пары спирта, этилен или галогены: хлор, бром, йод. Молекулы многоатомных газов поглощают фото- ны, не испуская электронов, а в качестве одноатомных добавок выбираются электроотрицательные газы – электроны захватываются такими атомами, об- разуя малоподвижные комплексы, которые уже не участвуют в разряде.

Счетная характеристика

Счетной характеристикой (рис. 6) называют зависимость скорости

n

I II III

Uнс Uн

Uк U

Рис. 6. Счетная характеристика счетчика Гейгера-Мюллера

счета n (при неизменных условиях облучения) от величины напряжения U .

Скоростью счета n называют число частиц, зарегистрированных в единицу

времени, т.е.

n = N/t , где N – полное число частиц, зарегистрированных за

время измерения t.

Вследствие малой чувствительности электронного устройства для ре-

гистрации импульсов, при напряжениях на счетчике U < U 4

(см. рис. 5), когда

условия возникновения самостоятельного (незатухающего) разряда еще не

выполняются и амплитуды импульсов DU

n равна нулю.

очень малы, скорость счета частиц

При напряжениях начала счета

U HC ,

слегка превышающих

U 4 ,

из-за

значительного разброса импульсов по амплитудам, возникающим из-за флуктуаций в развитии и гашении разряда, заметная доля импульсов может оказаться несосчитанной пересчетным устройством. При дальнейшем повы- шении напряжения амплитуда импульсов растет, относительный вклад флук- туаций уменьшается, что приводит к быстрому нарастанию скорости счета в

области 1 от U HC

до U H

(рис.6). При U H < U < U K

амплитуды импульсов DU

выравниваются и скорость счета практически не зависит от приложенного к счетчику напряжения. Это так называемое плато – рабочая часть счетной характеристики. Счетчики хорошего качества имеют плато протяженностью

DU = UK -UH

не менее 100 В, а скорость счета в ее пределах изменяется не бо-

лее, чем на 3 -5%

(обл.II,рис.6).

В области III при

U > U K

скорость счета возрастает, что связано глав-

ным образом с "краевым эффектом", т.е. увеличением у концов анода элек- трического поля из-за конечной длины счетчика и возникновения условий для самопроизвольных разрядов (ложные импульсы). При еще больших на- пряжениях число ложных импульсов резко возрастает и в счетчике возникает непрерывный разряд, неподдающийся гашению при постоянном напряжении.

ВНИМАНИЕ!

Работа счетчика Гейгера-Мюллера в области III

может привести к его выходу из строя.

Рабочее DU

напряжение счетчика выбирают на середине плато. Так

как длина плато, напряжения начала счета

U HC , начала UH

и конца UK

плато

являются индивидуальными характеристиками счетчика, то для выбора ра-

бочего напряжения необходимо снять счетную характеристику.

При отсутствии источника ионизирующего излучения искусственного происхождения счетчик может фиксировать импульсы космического излуче-

ния, фонового излучения Земли и т.д. Скорость счета в этом случае называют фоном счетчика. Для снижения постороннего фона счетчик и исследуемый радиоактивный препарат при необходимости экранируют, помещая их в

свинцовый "домик".

Выбор режимов измерений

При любом физическом измерении результат, полученный на опыте, несколько отличается от действительного значения измеряемой величины. Погрешности измерений складываются из ошибок, связанных с несовершен-

ством методики измерений и неточностью калибровки приборов (эти ошибки принято называть систематическими), и из случайных ошибок эксперимента, изменяющих свою величину и знак от опыта к опыту. Их частным случаем являются так называемые статистические ошибки, они вызываются флуктуа- циями самой измеряемой величины. К числу флуктуирующих величин отно- сятся: плотность потока частиц, падающих на счетчик, количество ядер, ис- пытывающих радиоактивное превращение за определенный промежуток времени, и т.д.

Рассмотрим опыт по определению интенсивности потока от некоторого радиоактивного препарата. Если провести ряд опытов по измерению числа

частиц, то обнаружится, что найденные числа заметно отличаются друг от друга. Условия эксперимента часто оказываются такими, что число радиоак- тивных ядер можно считать бесконечно большим. Тогда вероятность полу-

чить при измерении то или иное число частиц подчиняется распределению Пуассона [1-4]. На самом деле многократные измерения производятся редко. Наибольший интерес представляет собой ожидаемое отличие результата, по-

лученного при одиночном измерении, от истинного значения. Из теории сле- дует, что среднеквадратичное отклонение для нормального распределения числа отсчетов за некоторый интервал времени равно корню квадратному из

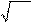истинного числа отсчетов за тот же интервал: s =

No .

Однако почти всегда

истинное значение неизвестно, поэтому в формулу для определения стан-

дартной ошибки приходится подставлять не истинное

No ,

а измеренное

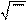среднее значение N , так что s= N .

При достаточно большом числе ядер, испытывающих радиоактивный распад , среднее значение числа отсчетов N может быть заменено на измеренное однократно значение N :

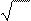
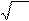s= N .

(6)

Формула (6) показывает, что, как правило (с вероятностью 68% ), сред-

нее число зарегистрированных частиц заключено в интервале

N - N

< N < N + N .

чине

Часто стандартную ошибку выражают в процентах к измеряемой вели-

d

N

= N ×100% = 100% .

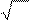
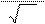
N N

Это соотношение определяет число регистрируемых частиц, необходи-

мое для достижения нужной точности. Так,

N = 102

гарантирует ошибку в

10%, а при

N = 104

ошибка не превысит 1% (предполагается, что время изме-

рено точно).

Пусть за время t зарегистрировано N частиц, тогда среднее число час-

тиц, зарегистрированных в единицу времени (скорость счета), равно

Среднеквадратичная ошибка в определении скорости счета n равна

n = N/t.

d

а относительная ошибка

= n ,

s

n t

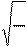
(7)

s 1

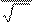= n = =

n n N

1 .

n × t

(8)

Из формулы (8) видно: точность измерения скорости счета растет с

увеличением времени измерений (при постоянной скорости счета

n).

Так как

время реального эксперимента всегда ограничено, то невозможно сделать ошибку в определении измеряемой величины меньше некоторого минималь- ного значения. Становится очевидной важность правильного планирования эксперимента с целью получения максимальной точности измерений.

Не все зарегистрированные счетчиком частицы имеют одинаковую природу. Часть их испущена радиоактивным источником, часть представляет

собой фоновое излучение.

Таким образом, если источник излучения и счетчик не экранированы,

скорость счета частиц nu

учетом фона

ионизирующего излучения должна находиться с

nu = n -nf,

(9)

где n и nf

– суммарная и фоновая скорости счета соответственно.

Среднеквадратичная ошибка в определении n находится по известным формулам подсчета среднеквадратичной ошибки функции измеряемых вели-

чин Z =

f ( x1, x2 ,...xk )

å

k

s

=

2

z

i =1

( df dxi

x

) 2 s2 .

i

(10)

Из формул (9) и (10) следует, что среднеквадратичная погрешность s

n

u

в определении скорости счета nu

только от радиоактивного источника равна

s = s2 +s2 ,

(11)

nu n nf

s

где n

n

и s определяются формулой (7); t – время измерения суммарного

f

излучения (источник + фон); t f

– время измерения фона.

Относительная погрешность

источника без учета фона равна

d определения скорости счета частиц от

n

u

n +nf

t tf

= .

d

n

u

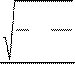n -nf

(12)

Поставим перед собой задачу определения скорости счета от источника

n

n

u

n с максимальной точностью (минимальными погрешностями s и d )

u u

при условиях, что задано полное время измерений

T = t +tf,

(13)

а скорость счета n и nf

известны и постоянны во время измерений.

Как долго нужно проводить отдельные измерения? Минимизируя фор- мулу (11) или (12), при условии (13), получим, что погрешности минималь- ны, если время отдельных измерений выбрано в отношении

t = n .

(14)

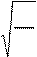tf nf

Так, например, если суммарная скорость счета (источник + фон) равна

f

n = 900c -1 , а скорость счета фона

n = 100c -1 , то на измерение суммарной

скорости счета n следует затратить в три раза больше времени, чем на изме-

рение фона.

Часто ставят иную задачу: найти наименьшие времена t и

tf, при ко-

торых относительная погрешность измерения скорости счета от источника

d не превышает заданную d ( d £d

) в предположении, что скорость счета

nu 0 nu 0

n и nf

постоянны во время измерений. По сути задача сводится к миними-

зации полного времени измерений (13) при заданной d

n

u

минимизацию, получим

= d (12). Выполнив

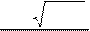n + nf×n

t ³ ,

(15)

0 f

d 2 (n - n ) 2

nf+

t ³

nf×n

,

(16)

0 f

f d 2 (n - n ) 2

где знак «равно» соответствует значениям времен t и tf

данной погрешности d0 .

для достижения за-

В дальнейшем задачу о наилучшем распределении времени студент решает самостоятельно. При подсчете полной ошибки не следует упускать и другие источники ошибок (точность в определении толщины фольги, рас- стоянии и т.п.). Все квадратичные ошибки складываются в соответствии с формулой (10).