Математичний апарат термодинаміки

Державний вищий навчальний заклад

“ЗАПОРІЗЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ”

Міністерства освіти і науки України

О.Ю. ОСИПОВ, А.М. АНДРЄЄВ

ТЕРМОДИНАМІКА

І СТАТИСТИЧНА ФІЗИКА

В ПРИКЛАДАХ І ЗАДАЧАХ

Рекомендовано

Міністерством освіти

і науки України

як навчальний посібник

для студентів

вищих навчальних закладів

ЗАПОРІЖЖЯ

УДК 535+531.19(076)

ББК 22.35 я 73

О 74

Рецензенти:

Академік НАН України, доктор фізико-математичних наук, професор,

завідувач кафедри молекулярної фізики КНУ ім. Т.Г. Шевченка

Л.А. Булавін

Доктор фізико-математичних наук, професор,

перший проректор Класичного приватного університету

О.М. Горбань

Доктор технічних наук, професор, завідувач кафедри фізики

Дніпропетровського національного університету залізничного транспорту

В.О. Заблудовський

Рекомендовано Міністерством освіти і науки України

як навчальний посібник для студентів вищих навчальних закладів

Лист № 1/11 – 3873 від 11.05.2010 р.

Осипов О.Ю.

О 74 Термодинаміка і статистична фізика в прикладах і задачах: навчальний посібник / О.Ю. Осипов, А.М. Андрєєв. – Запоріжжя, Запорізький національний університет, 2010. – 220 с.

ISBN

Навчальний посібник містить разом із необхідними теоретичними відомостями з термодинаміки і статистичної фізики широке коло характерних задач з розв’язанням, а також задачі для самостійного розв’язування. Посібник призначений для студентів фізичних спеціальностей вищих навчальних закладів.

УДК 535+531.19(076)

ББК 22.3 я 73

© Запорізький національний університет, 2010

ISBN© Осипов О.Ю., Андрєєв А.М., 2010

Передмова

Навчальний посібник призначений для студентів фізичних спеціальностей класичних університетів і відповідає курсу теоретичної фізики “Термодинаміка і статистична фізика”.

Метою авторів було надати студентам можливість під час самостійної роботи повторити основні питання (поняття, закони, методи) курсу та засвоїти їх, розібравши відповідний перелік задач.

Перша частина посібника присвячена термодинаміці, друга – статистичній фізиці. Матеріал подається за розділами, кожен з яких містить теоретичні відомості, розв’язання характерних задач та задачі для самостійного розв’язування, більшість з яких є авторськими.

У посібнику розглядаються переважно рівноважні термодинамічні системи. Останній же розділ у першій частині присвячений нерівноважній термодинаміці, в ньому висвітлені сучасні досягнення, які вже стали класичними.

Навчальний посібник відповідає освітньо-професійній програмі галузевого стандарту освіти напряму підготовки 6.040203 – фізика в частині її змістових модулів.

Частина перша

ТЕРМОДИНАМІКА

Розділ 0

ОСНОВНІ ПОНЯТТЯ І ВИХІДНІ ПОЛОЖЕННЯ

ТЕРМОДИНАМІКИ

Предмет термодинаміки. Термодинаміка є одним із методів вивчення багаточастинкових систем та фізичних і хімічних процесів, що відбуваються в цих системах. Під частинками, які складають таку, найчастіше макроскопічну систему, завжди розуміють саме мікрочастинки. Ними можуть бути атоми, молекули, іони, електрони, фотони тощо. Сутність термодинаміки як методу полягає в тому, що він не спирається ні на які модельні уявлення про внутрішню, атомно-молекулярну (або на більш глибокому мікроскопічному рівні) структуру об’єкту вивчення. В цьому відношенні він є чисто описовим або, як ще кажуть, феноменологічним методом. Як наслідок, завданням термодинамічного методу є встановлення зв’язків і закономірностей між величинами, які безпосередньо спостерігаються (вимірюються в макроскопічних дослідах). До таких належать: тиск, об’єм, температура, концентрація розчину, напруженості та індукції електромагнітного поля тощо.

Важливо підкреслити, що цей метод не має чітко обмеженої галузі фізичних явищ для вивчення, яку мають механіка, електродинаміка, оптика та інші розділи фізики. Термодинамічним методом можна вивчати будь-які системи, що складаються з достатньо великої кількості частинок: гази, рідини, тверді тіла, атомні ядра (з великою кількістю нуклонів), світлове випромінювання тощо. При цьому масштабом в оцінках за шкалою кількості частинок 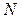, як правило, є число Авогадро 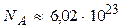моль^-1.

Не вдаючись до обговорення переваг і недоліків термодинаміки як методу, зауважимо, що більш проста її частина вивчає макроскопічні закономірності теплового руху в рівноважних системах. Цей розділ називають рівноважною термодинамікою або просто термодинамікою на відміну від нерівноважної термодинаміки, якій буде присвячена остання глава.

Основні поняття термодинаміки. Термодинаміка оперує фізичними величинами, які кількісно виражають ті чи інші макроскопічні ознаки багаточастинкової системи. Такі величини називають термодинамічними параметрами або просто параметрами системи. До них належать вже перелічені тиск, об’єм, температура, концентрація, напруженості фізичних полів тощо.

Параметри в термодинаміці розділяють на внутрішні і зовнішні. Зовнішні параметри (позначатимемо 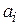) – це величини, які визначаються розташуванням об’єктів, що не входять в саму систему; наприклад: об’єм 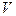системи (він визначається розташуванням зовнішніх по відношенню до неї тіл - стінок, скажімо, судини), напруженість того чи іншого поля (залежить від розташування джерел поля, які також до системи не входять) і т. п. Зовнішні параметри звичайно є функціями координат зовнішніх тіл. Величини, які визначаються спільним рухом і розподілом в просторі частинок, що входять в систему, називають внутрішніми параметрами (позначатимемо 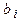). До таких належать густина, температура, енергія, поляризація, тиск та ін. Звідси випливає, що внутрішні параметри визначаються і значеннями зовнішніх параметрів.

Сукупність незалежних термодинамічних параметрів задає стан системи. Величини, які повністю визначаються станом системи (тобто сукупністю незалежних параметрів), називаються функціями стану. Стан називається стаціонарним, якщо параметри системи з плином часу не змінюються. Якщо в стаціонарному стані в системі відсутні потоки будь-яких фізичних величин, то говорять про рівноважний стан або стан термодинамічної рівноваги, так само, як і про рівноважні параметри цієї системи.

Внутрішні параметри поділяються на інтенсивні та екстенсивні. Параметри, що безпосередньо не залежать від маси або кількості частинок в системі, називаються інтенсивними (тиск, температура, ...). Параметри, пропорційні масі або кількості частинок в системі, називаються екстенсивними (або адитивними) параметрами (енергія, об’єм, ентропія, ...). Екстенсивні параметри характеризують систему як ціле, тобто вони є глобальними характеристиками. Інтенсивні ж параметри в цьому розумінні є локальними характеристиками системи.

Вихідні положення термодинаміки. Відомо, що фізика вивчає найпростіші форми руху матерії, і основною його мірою є енергія. Система, яка не обмінюється з зовнішніми тілами ні енергією, ні частинками, називається ізольованою. В термодинаміці постулюється, що в такій системі завжди існує стан термодинамічної рівноваги, в який вона приходить через певний проміжок часу і з якого самодовільно вийти не може. Це твердження становить собою перший або основний постулат термодинаміки.

Зрозуміло, що при тепловому контакті двох систем стани останніх можуть змінюватися аж до приходу їх до загального (спільного) стану рівноваги. З цього логічно випливає, що стан рівноваги системи визначається не тільки значеннями зовнішніх параметрів 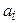. Необхідна величина, що характеризує внутрішній стан системи і регулює вирівнювання станів при їх тепловому контакті. Ця величина, що виражає інтенсивність внутрішнього руху в системі, називається температурою. Вихідне положення про існування температури як особливої функції стану системи в рівновазі є другим постулатом термодинаміки. Іноді його називають нульовим началом термодинаміки. Не обговорюючи вибір шкали температур, в подальшому будемо користуватися лише так званою абсолютною шкалою, позначаючи температуру за нею через 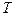. З другого постулату випливає, що стан термодинамічної рівноваги визначається сукупністю зовнішніх параметрів і температурою.

Внутрішня енергія системи, робота і теплота. Повна (сумарна) енергія частинок системи поділяється на внутрішню і зовнішню. Частина енергії, що складається з енергії руху системи як цілого та потенціальної енергії системи в полі зовнішніх сил, називається зовнішньою енергією. Решта енергії системи називається внутрішньою енергією, яку будемо позначати через 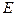. Термодинаміка цікавиться лише внутрішньою енергією. Отже, внутрішня енергія є внутрішнім параметром і при рівновазі повинна бути функцією зовнішніх параметрів 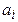і температури :

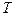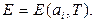(0.1)

При взаємодії термодинамічної системи з навколишнім середовищем відбувається обмін енергією. При цьому існують два різних способи передачі енергії від системи до зовнішніх тіл і навпаки: зі зміною зовнішніх параметрів і без їх зміни.

Енергія, передана системою зі зміною її зовнішніх параметрів, називається роботою, яку в подальшому будемо позначати 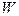. Енергія, передана системою без зміни її зовнішніх параметрів, називається кількістю теплоти і позначається 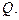Важливо, що ці два способи не є рівноцінними (певною мірою симетричними). Якщо робота може безпосередньо піти на збільшення будь-якого виду енергії (електромагнітної, пружної і т.п.), то кількість теплоти безпосередньо, без попереднього перетворення в роботу, може піти лише на збільшення внутрішньої енергії системи.

Суттєво, що робота 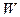і кількість теплоти 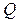характеризують тільки процес, в якому бере участь система. Стану ж системи не відповідає будь-яке значення 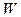або 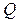. Тому не слід говорити про запас теплоти чи роботи в тілі.

Прийнято вважати роботу 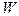додатною, якщо вона виконується системою над зовнішніми тілами. Кількість теплоти 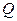вважається додатною, якщо енергія додається системі (без зміни зовнішніх параметрів).

При нескінченно малій рівноважній зміні параметрів 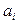робота, що здійснюється системою, дорівнює

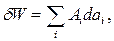(0.2)

де 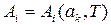- так звана узагальнена сила, що відповідає зовнішньому параметру .

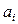Як випливає з визначення роботи, і як видно з (0.2), до цього виразу не входить диференціал температури 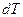. Це призводить до того, що вираз (0.2) не є в загальному випадку повним диференціалом певної функції параметрів, які описують стан системи. Через це елементарну роботу позначають 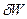, а не .

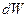Розглянемо приклади виразів для 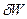в деяких конкретних випадках. Якщо 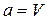, тоді 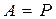(тиск газу або рідини) і

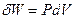. (0.3)

Елементарна робота сил поверхневого натягу при зміні площі поверхні на 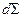дорівнює

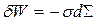; (0.4)

тут 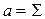, 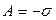– коефіцієнт поверхневого натягу із знаком “–”.

Елементарна робота у випадку процесу намагнічування записується у вигляді

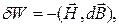(0.5)

де 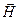– напруженість, 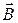– індукція магнітного поля.

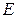Рівняння стану. Друге вихідне положення термодинаміки дозволяє розглядати рівноважні внутрішні параметри як функції зовнішніх параметрів і температури. Якщо внутрішнім параметром є внутрішня енергія , то рівняння

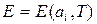(0.6)

називається калоричним рівнянням стану.

Якщо внутрішнім параметром 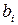є спряжена зовнішньому параметру а_і узагальнена сила 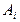, то рівняння

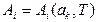(0.7)

називають термічними рівняннями стану.

Загальна кількість термічних і калоричних рівнянь стану дорівнює кількості степенів вільності системи, тобто кількості незалежних параметрів, що характеризують (і визначають) її стан. Якщо термічне і калоричне рівняння стану відомі, то за допомогою начал термодинаміки можна встановити усі термодинамічні властивості системи. Вивести самі рівняння стану з начал не можна. Ці рівняння встановлюються з досліду або виводяться методами статистичної фізики.

При вивченні властивостей рівноважних систем термодинаміка найчастіше розглядає так звані прості системи. Простою називається термодинамічна система з постійним числом частинок, стан якої визначається єдиним зовнішнім параметром 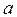і температурою 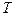. Термічне і калоричне рівняння стану при цьому матимуть вигляд

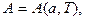(0.8)

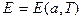. (0.9)

Якщо, скажімо 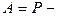тиск, а 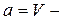об’єм системи, то ці рівняння стають більш конкретними:

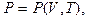(0.10)

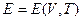. (0.11)

Для ідеального газу термічним рівнянням стану є рівняння Менделєєва-Клапейрона

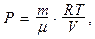(0.12)

де 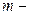маса газу, 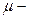молярна маса, 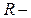газова стала. Калоричним рівнянням його стану є рівняння

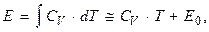(0.13)

де 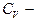теплоємність газу при постійному об’ємі. Для реальних газів емпірично встановлено понад сто термічних рівнянь станів. Найбільш простим з них є рівняння Ван-дер-Ваальса:

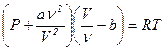, (0.14)

де 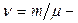число молів; 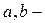сталі, що залежать від конкретного газу, але не залежать від 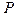і .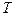

Більш сучасна форма термічного рівняння стану для реального газу дається у вигляді розкладання в ряд за степенями густини 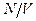газу:

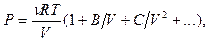(0.15)

де 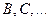є функціями 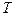і називаються віріальними коефіцієнтами. Саме рівняння (0.15) називається віріальним рівнянням.

У термодинаміці реальних газів часто розглядаються також такі термічні рівняння стану (для 1 моля):

рівняння Бертло

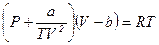, (0.16)

рівняння Клаузіуса

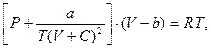(0.17)

перше рівняння Дітерічі

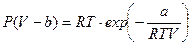, (0.18)

друге рівняння Дітерічі

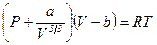. (0.19)

Вже з самого існування термічного рівняння стану можна отримати зв’язок між так званими термічними коефіцієнтами:

розширення

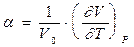, (0.20)

стиску

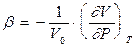, (0.21)

пружності

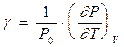; (0.22)

тут 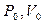– тиск і об’єм системи при .

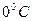Наявність термічного рівняння стану призводить до того, що ці коефіцієнти не є незалежними один від одного, а зв’язані співвідношенням:

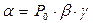, (0.23)

яке важливе для непрямого визначення 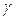, оскільки для твердих тіл і рідин практично неможливо нагріти їх без зміни об’єму.

Подібно до трьох термічних коефіцієнтів використовуються також три термодинамічних коефіцієнти:

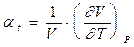, (0.24)

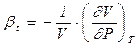, (0.25)

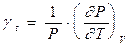, (0.26)

а також ізотермічний і адіабатичний модулі пружності:

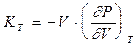, (0.27)

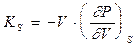, (0.28)

де S - ентропія.

Наведемо важливий для термодинаміки ідеальних газів емпіричний закон Джоуля, відповідно до якого внутрішня енергія ідеального газу при його ізотермічному розширенні не залежить від об’єму. Це твердження можна записати математично у вигляді:

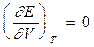. (0.29)

Раніше ми визначили ізольовану систему як таку, що не обмінюється з тілами, що її оточують ні енергією, ні речовиною. Якщо ж система має такий обмін, то вона називається відкритою. Якщо система не обмінюється з тілами, що її оточують, речовиною, але обмінюється енергією, то вона називається закритою. Якщо можливий обмін енергією в будь-якій формі крім теплоти, то така система називається адіабатною.

Наведемо на закінчення також калоричне рівняння стану газу Ван-дер-Ваальса:

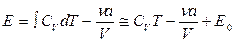. (0.30)

Розділ 1

МАТЕМАТИЧНИЙ АПАРАТ ТЕРМОДИНАМІКИ

Теоретичні відомості

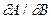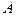Метод функціональних визначників Якобі (якобіанів). Типовим елементом математичного апарату термодинаміки є частинна похідна , де і 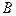- деякі термодинамічні параметри. Щоб підкреслити наявність інших “діючих” в конкретному розгляді параметрів, скажімо X та Y, вказану похідну прийнято записувати у вигляді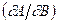 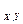.При цьому кажуть про похідну від 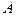за 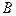при постійних X та Y (як це і повинно бути при формальному вирахуванні частинних похідних).

Для складних систем і систем зі змінною кількістю частинок, коли число присутніх в задачі термодинамічних параметрів досить велике, в розрахунках часто використовується так званий метод якобіанів, який дозволяє скоротити громіздкі підрахунки з похідними. Зокрема, цей метод формалізує процедуру переходу від одного набору незалежних змінних до іншого.

За визначенням якобіаном 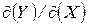перетворення 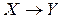змінних 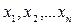до змінних 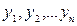називають визначник (DET) матриці 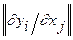і позначають

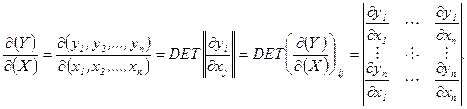(1.1)

Зокрема, при n = 2:

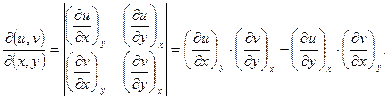(1.2)

Зрозуміло, що властивості якобіанів повторюють властивості визначника: лінійність по кожній із змінних 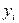, зміну знака при перестановці будь-якої пари змінних серед 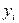чи 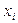. З визначення (1.1) також випливає:

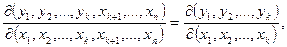(1.3)

зокрема,

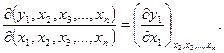(1.4)

Якщо перетворення 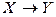відбувається за допомогою проміжного набору змінних 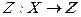і 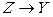, то з аналізу можна записати:

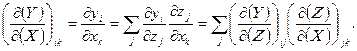(1.5)

Оскільки ця формула виражає відоме правило множення матриць, то на підставі рівності DET(A×B)=DET A×DET B (A,B - матриці) з (1.5) отримуємо важливу властивість якобіанів:

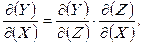(1.6)

яка дозволяє працювати з ними, як з дробами. Окремим випадком тотожності (1.6) є рівність

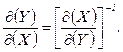(1.7)

З геометричної точки зору якобіан перетворення 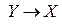пов’язує елементарні об’єми в просторах змінних 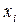та :

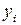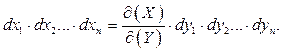(1.8)

Алгебраїчний сенс якобіана міститься в тому, що з обертання 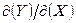в нуль у деякій області D значень змінних 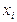випливає функціональна залежність в 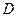величин 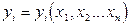. Інакше кажучи, в цьому випадку існує така нетривіальна функція 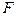змінних 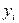, що в області 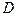виконується:

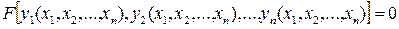. (1.9)

Лінійні диференціальні форми. Перетворення Лежандра. Вираз вигляду

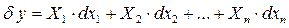, (1.10)

де 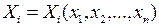, називається лінійною диференціальною формою (формою Пфаффа) змінних 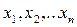. Вважатимемо, що величини 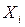є однозначні і неперервно диференційовані функції аргументів 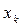. Щоб підкреслити, що ця форма в загальному випадку не є повним диференціалом, її прийнято позначати через 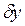замість dy. Можна говорити про інтегруючий множник 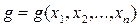, домноження якого на 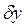перетворює праву частину (1.10) на повний диференціал. При 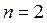форма 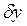завжди має інтегруючий множник. При 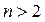інтегруючий множник для 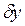в загальному випадку не існує.

У методі термодинамічних потенціалів (див. розділ 5) істотно використовується властивість повного диференціала функції кількох змінних. При цьому функцію 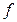називають характеристичною функцією змінних 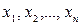, якщо її повний диференціал 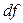виражається тільки і тільки через диференціали 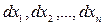цих змінних:

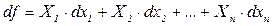; (1.11)

тоді 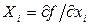. З математичної точки зору ця ситуація тривіальна. Однак в термодинаміці набір незалежних параметрів 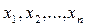часто виявляється заданим і саме під нього треба підшукувати певну функціональну конструкцію 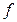, яка б задовольняла (1.11). Такий підбір функції 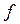не є завжди очевидним. Крім того існує і обмеження на вирази типу (1.11), яке випливає з закону збереження енергії. Цим обмеженням є фундаментальне рівняння першого начала термодинаміки.

Існує простий алгоритм знаходження нової функції, яка залишається характеристичною при заміні 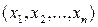на більш придатний (з точки зору дослідника) набір аргументів. Так, якщо замість 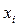в нових умовах незалежною виявляється величина 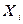(узагальнена сила, що відповідає зовнішньому параметру 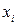), то перетворення 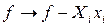визначає нову функцію :

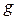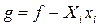, (1.12)

яка стає характеристичною функцією вже змінних 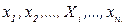. Дійсно, диференціюючи (1.12), з урахуванням (1.11) маємо:

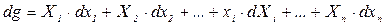. (1.13)

Перетворення такого роду називають перетвореннями Лежандра. Вони фактично міняють ролями незалежні і залежні змінні, не порушуючи при цьому властивості характеристичності нової функції.

Однорідні функції і їх властивості. Функція 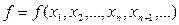, якій притаманна властивість

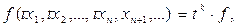(1.14)

називається однорідною функцією степеня 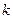відносно змінних 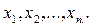Теорема Ейлера про однорідні функції стверджує, що

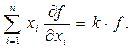(1.15)

Зокрема, якщо 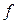є однорідною функцією степеня 1 відносно всіх своїх змінних, то звичайна формула для повного диференціала

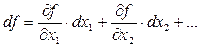
справедлива і для скінченних значень величин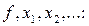

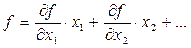. (1.16)