Преобразование сигналов в линейных и нелинейных каналах

Системой наз-т совокупность физических объектов, между которыми существуют определенные взаимодействия. Система стационарна, если ее выходная реакция не зависит от того, в какой момент времени поступает входной сигнал. Если Т — оператор стационарной системы, то 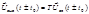при любом значении t₀. Стационарные системы называют также системами с постоянными во времени параметрами.

Если же свойства системы не инвариантны относительно выбора начала отсчета времени, то такую систему называют нестационарной(системой с переменными во времени параметрами или параметрической системой).

Если оператор системы таков, что справедливы равенства

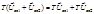
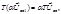
где α — произвольное число, то данная система называется линейной. Если эти условия не выполняются, то говорят, что система является нелинейной.

импульсной характеристикойсистемы называется функция h(t), являющаяся откликом системы на входной сигнал δ(t). Это означает, что функция h(t) удовлетворяет уравнению h(t)=Tδ(t).

Инт-л Дюамеля: u_вых(t)= 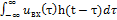. Это соотношение свидетельствует о том, что выходной сигнал линейной стационарной системы представляет собой свертку двух функций — входного сигнала и импульсной характеристики системы.

Пусть на входе линейной стационарной системы действует сигнал, изображаемый функцией Хевисайда Ϭ(t). Выходную реакцию g(t)=TϬ(t) принято называть переходной характеристикойсистемы.Поскольку система стационарна, переходная хар-ка инвариантна относительно временного сдвига: g(t-t₀)=TϬ(t-t₀).

Между импульсной и переходной характеристиками имеется тесная связь. Действительно, так как δ(t)=dσ/dt, то

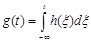
Покажем что комплексный сигнал u_вх(t) = exp (jωt) при любом значении частоты ω есть собственная функция cтaциoнaрнoгo оператора. Для этого воспользуемся интегралом Дюамеля вида (10.4) и вычислим

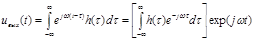
Здесь частотным коэффициентом передачисистемы является комплексное число, являющееся собственным значением системного оператора

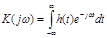
Частоный коэф-т и импульсная хар-ка связаны м/у собой преобразованием Фурье:

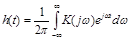
Часто пользуются представлением частотного коэффициента передачи в показательной форме:

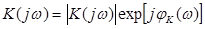
Обе входящие сюда вещественные функции носят специальные названия:|K(jω)| — амплитудно-частотная характеристика (АЧХ), φ_K(ω) - фазочастотная характеристика (ФЧХ) системы.

Спектральный метод анализа прохождения радиотехнических сигналов через линейные стационарные системы - виду целый комплекс математических приемов, в основе которых лежит использование свойств частотного коэффициента передачи системы.

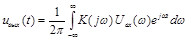
Преобразований случайных процессов при их прохождении через динамические системы (как с регулярными, так и со случайно меняю­щимися параметрами) связано с решением задач двух типов: определение кор­реляционной функции (спектральной плотности мощности) отклика Y(t) на выходе системы, заданной своими характеристиками, по данной корреляцион­ной функции (или спектральной плотности мощности) входного воздействия X(t) определение многомерного распределения вероятностей отклика У(t) на выходе системы по многомерному распределению входного воздействия X(t).

Случайную линейную систему (или линейный канал) можно описать случайной импульсной хар-кой G(t,τ), представляющей случайную функцию двух аргументов: t (момента наблюдения реакции) и t (времени, прошедшего с момента подачи d-импульса на вход цепи). Случайный линейный канал можно характеризовать также случайной пере­даточной функцией переменных ω и t