Последовательности одиночных сигналов

В радиотехнических системах используются, как правило, последовательности одиночных сигналов (рис. 1.32):

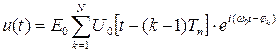, 0 ≤ t ≤ NT_п

где ψ_k -начальные фазы радиоимпульсов, принимаемые в дальнейшем одинаковыми и равными φ₀ .

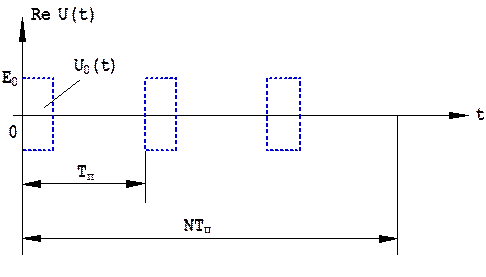
Рис.1.32. Последовательность N одиночных сигналов.

Корреляционная функция закона модуляции последовательности одиночных сигналов

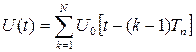
может быть представлена произведением корреляционной функции огибающей последовательности r_N(τ) и бесконечной последовательности корреляционных функций закона модуляции одиночных сигналов (рис.1.33)

.

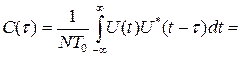
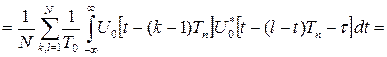
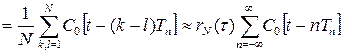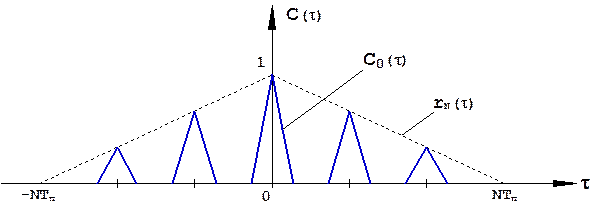
Рис.1.33. Корреляционная функция закона модуляции последовательности одиночных сигналов.

Корреляционная функция прямоугольной огибающей последовательности является треугольной

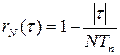, |τ| ≤ NT_п .

Энергетический спектр закона модуляции последовательности одиночных сигналов может быть представлен произведением энергетического спектра закона модуляции одиночного сигнала S₀(ω) и так называемого междупериодного энергетического спектра S_N(ωT_п), который является результатом размножения по частоте с интервалом, равным частоте повторения F_п = 1 / T_п, энергетического спектра огибающей последовательности S_N(ω) (рис.1.34):

, .

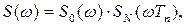
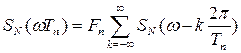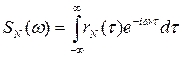Таким образом, энергетический спектр последовательности одиночных сигналов является гребенчатым. Ширина его зубцов определяется шириной энергетического спектра огибающей последовательности и оказывается обратно пропорциональной продолжительности последовательности NT_п:

.

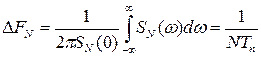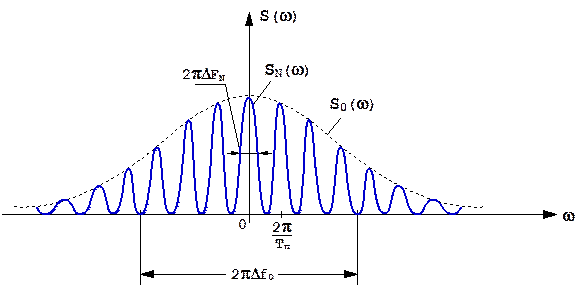
Рис.1.34. Энергетический спектр закона модуляции последовательности одиночных импульсов.

Общая протяжённость энергетического спектра последовательности одиночных сигналов определяется шириной спектра одиночного сигнала Δf₀ , а эффективное число зубцов равно Δf₀T_п.

Функция неопределённости последовательности радиоимпульсов имеет многолепестковую структуру по всей плотности τ, F. Действительно, её сечение вдоль оси τ определяется квадратом модуля корреляционной функции

.

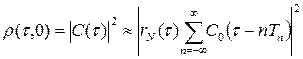С учётом того, что время корреляции одиночного радиоимпульса много меньше периода повторения, выражение для ρ(τ,0) принимает вид:

.

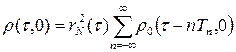Сечение функции неопределенности вдоль оси F описывается гребенчатой функцией, характеризующей нормированный энергетический спектр квадрата амплитудного закона модуляции последовательности радиоимпульсов

.

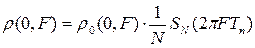Соответствующая диаграмма неопределённости последовательности одиночных сигналов изображена на рис. 1.35.

Рис.1.35. Диаграмма неопределенности непрерывного модулированного сигнала.

Протяженность лепестков ρ(τ,F) по времени и частоте обратно пропорциональна соответственно ширине спектра радиоимпульса и длительности последовательности. Интервалы между лепестками анализируемой функции неопределённости взаимосвязаны друг с другом, что исключает возможность независимого изменения их. Так, увеличение интервала вдоль оси времени за счёт увеличения периода повторения T_п неизбежно приводит к сокращению интервала вдоль оси частот, величина которого равна F_п. Эффективная протяженность диаграммы неопределённости вдоль оси τ определяется длительностью последовательности NT_п, а протяжённость вдоль оси F обратно пропорциональна длительности одиночного сигнала 1/T_п.

В случае непрерывного сигнала (Т₀ = T_п) функция неопределённости характеризуется многолепестковой структурой не по всей плоскости τ, F а лишь вдоль оси τ, поскольку нормированный энергетический спектр квадрата амплитудного закона модуляции последовательности примыкающих друг к другу радиоимпульсов не является гребенчатым, а имеет всего один лепесток, ширина которого вдоль оси частот обратно пропорциональна длительности последовательности

.

Диаграмма неопределённости непрерывного сигнала изображена на рис.1.36.

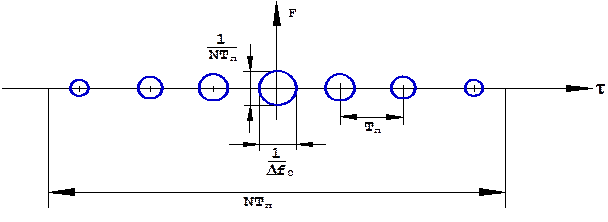
Рис.1.36. Диаграмма неопределенности непрерывного модулированного сигнала.

Заканчивая анализ функции неопределённости последовательности одиночных сигналов и, несколько забегая вперёд, уместно зафиксировать, что неопределённость, которая характеризуется функцией ρ(τ,F) относится, во-первых, к разрешающей способности по времени запаздывания Δt_r = Δτ = 1/Δf₀ и доплеровской частоте ΔF_Д = ΔF_N = 1/NT_п и во-вторых, к интервалу однозначного определения времени запаздывания t_{r одн} = T_п и доплеровской частоты F_{Д одн} = 1/T_п. В случае непрерывного сигнала Т₀=T_п интервал однозначного определения доплеровского смещения частоты не ограничен F_{Д одн} → ∞.

Монохроматический сигнал

Монохроматический сигнал представляет собой немодулированное (U(t)=1) гармоническое колебание (рис.1.37):

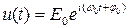
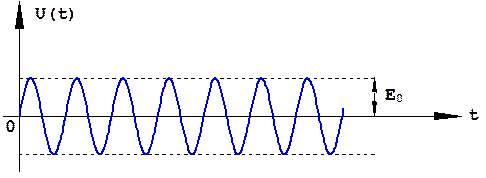
Рис.1.37. Монохроматический сигнал.

Его можно интерпретировать либо как одиночный простой прямоугольный радиоимпульс бесконечно большой длительности, либо как бесконечную когерентную (синфазную) последовательность простых прямоугольных радиоимпульсов с длительностью, равной периоду повторе­ния. Корреляционная функция монохроматического сигнала

,

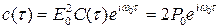где C(τ) = 1 – корреляционная функция закона модуляции монохроматического сигнала (рис.1.38).

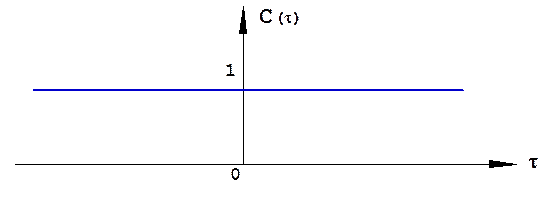
Рис.1.38. Корреляционная функция закона модуляции монохроматического сигнала.

Энергетический спектр рассматриваемого сигнала, равный

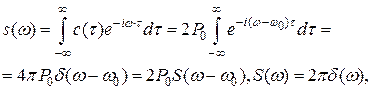
имеет единственную спектральную составляющую на частоте ω₀ (рис.1.39).

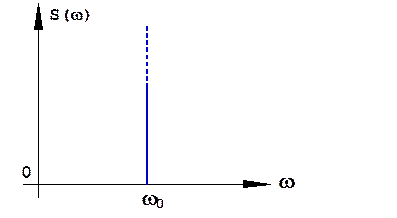
Рис.1.39. Энергетический спектр монохроматического сигнала.

Функция неопределенности монохроматического сигнала имеет единственный лепесток, бесконечно узкий вдоль оси частот и беско­нечно широкий вдоль оси времени (рис.1.40).

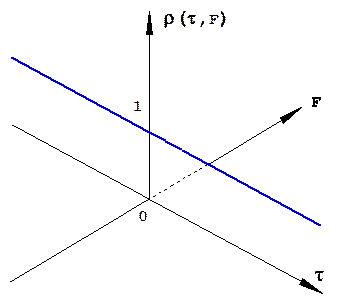
Рис.1.40. Функция неопределенности монохроматического сигнала.

Принятый сигнал

Принятый сигнал

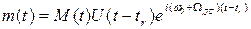
имеет не только первичную регулярную модуляцию U(t) = |U(t)|e^iψ(t), но и приобретенного в результате отражения, рассеяния, распространения радиоволн вторичную случайную модуляцию.

Корреляционная функция принятого сигнала представляется как результат двухэтапного усреднения - статистического усреднения случайной временной структуры (обозначается чертой сверху) и усреднения регулярной временной структуры:

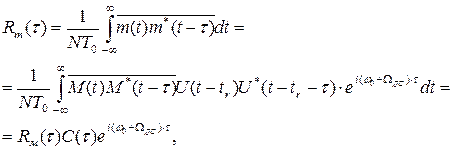
где 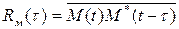есть корреляционная функция комплексной огибающей принятого сигнала.

Статистическое усреднение комплексной огибающей M(t), являющейся согласно физическим представлениям эргодическим случайным процессом (для которого усреднение по времени и по ансамблю реализации эквивалентны), предполагает усреднение по множеству реализаций, продолжительность которых ограничена временем наблюдения объекта наблюдения (сигнала) в пределах одного элемента разрешения. Иными словами, статистическое усреднение предполагает усреднение по множеству реализации. Корреляционная функция комплексной огибающей M(t) является характеристикой как амплитудных, так и фазовых его флуктуации. Она определяется экспериментально. Результаты многочисленных экспериментальных исследований свидетельствуют о возможности её аппроксимации удобной в практических приложениях экспоненциальной кривой (рис. 1.41.):

,

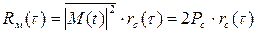где 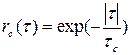– нормированная корреляционная функция флуктуаций принятого сигнала.

Время корреляции флуктуации принятого сигнала τ_с зависит от многих факторов (диапазона частот, размеров объекта наблюдения, динамики его движения, вибраций его поверхности, условий распространения радиоволн и др.) и может изменяться в широком диапазоне от единиц миллисекунд до единиц секунд.

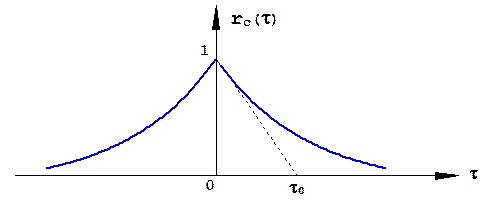
Рис.1.41. Нормированная функция флуктуации принятого сигнала.

Таким образом, корреляционная функция принятого сигнала окончательно может быть представлена следующим выражением:

.

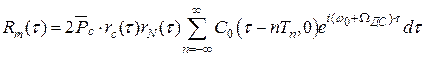Она отличается от корреляционной функции излучаемой нефлуктуирующей ограниченной последовательности одиночных сигналов наличием дополнительного сомножителя r₀(τ). Произведение r_N(τ)·r_C(τ) характеризует нормированную корреляционную функцию огибающей ограниченной по времени и флуктуирующей по амплитуде и фазе последовательности одиночных сигналов:

r_NC(τ) = r_N(τ)·r_C(τ).

Энергетический спектр принятого сигнала представляется произведением энергетического спектра одиночного сигнала и междупериодного энергетического спектра флуктуирующей ограниченной последовательности

,

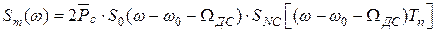причем гребенчатый междупериодный энергетический спектр есть размноженный по частоте с интервалом, равным частоте повторения, энергетический спектр огибающей последовательности с учетом ограниченного времени наблюдения и флуктуации:

, .

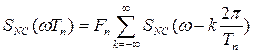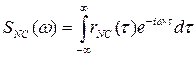Ширина зубцов энергетического спектра принятого сигнала, т.е. ширина энергетического спектра огибающей последовательности, определяется, во-первых, величиной, обратной времени наблюдения (продолжительности последовательности) и, во-вторых, шириной спектра флуктуации принятого сигнала:

.

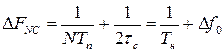Вероятностные свойства принятого сигнала определяются вероятностными характеристиками его комплексной огибающей. Наиболее полной характеристикой комплексной огибающей принятого, сигнала, которая вместе с тем является необходимой при решении целого ряда задач синтеза и анализа РТС, является многомерная плотность вероятности значений этого процесса, взятых в дискретные моменты времени.

Поясним физический смысл многомерной плотности вероятности на примере произвольного случайного процесса x(t). Каждая реализация этого процесса может быть представлена совокупностью его значений в дискретные моменты времени (x₁, x₂,…,x_N). Каждая такая совокупность значений процесса характеризуется многомерной плотностью вероятности p(x₁, x₂,…,x_N).

Если умножить плотность вероятности на dx₁ × dx₂×…×dx_N , то полученная величина будет характеризовать совместную вероятность следующего события: первый отсчет находится в промежут­ке между x₁ и x₁ + dx₁ , второй - в пределах между x₂ и x₂ + dx₂ и так далее:

x₁ < x(t₁) < x₁ + dx₁;

x₂ < x(t₂) < x₂ + dx₂;

……………………

x_N < x(t_N) < x_N + dx_N.

Поскольку величины x₁, x₂,…,x_N однозначно определяют всю реализацию, то величина

p(x₁, x₂,…,x_N) dx₁×dx₂×…×dx_N

представляет собой вероятность попадания реализации x(t) на "дорожку", определяемую дискретными значениями x_k (рис.1.42):

x_k < x(t_k) < x_k + dx_k.

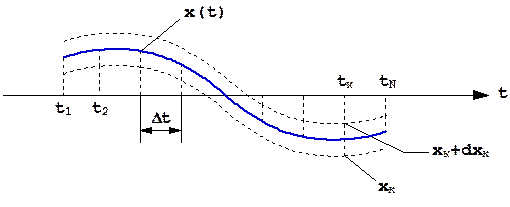
Рис. 1.42. Пояснение понятия многомерной плотности вероятности случайного процесса.

Благодаря тому, что случайный характер комплексной огибающей М(t) определяется множеством факторов при формировании принятого сигнала (процессы отражения, рассеяния, распространения), в силу предельной теоремы теории вероятностей (теоремы Ляпунова) комплексная огибающая М(t) представляет собой случайный процесс с многомерной плотностью вероятности

,

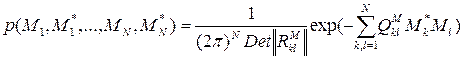где 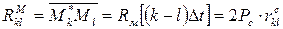есть элементы корреляционной матрицы (корреляционные моменты) дискретных значений, комплексной огибающей принятого сигнала, 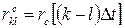- элементы нормированной корреляционной матрицы флуктуации принятого сигнала, 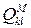- элементы матрицы, обратной 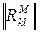, - определитель (детерминант) матрицы .

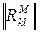Полагая в выражении многомерной плотности вероятности комплексной огибающей принятого сигнала число отсчетов N = 1, находим совместное распределение вероятности мгновенных значений комплексной огибающей М₁ и М₁^* (для одного момента времени):

.

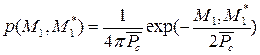Определение совместного распределения вероятности квадратурных составляющих комплексной огибающей принятого сигнала x_м и y_м связано с функциональным преобразованием (М₁ , М₁^*) → (x_м , y_м).

Учитывая, что М₁ = x_м + iy_м, М₁^* = x_м – iy_м, якобиан такого преобразования равен:

.

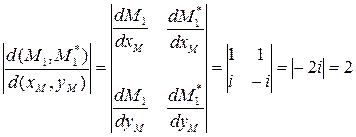Поэтому совместное распределение вероятности квадратурных составляющих комплексной огибающей принятого сигнала определяется выражением

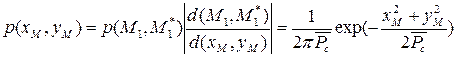
и изображается колоколообразной поверхностью (рис. 1.43).

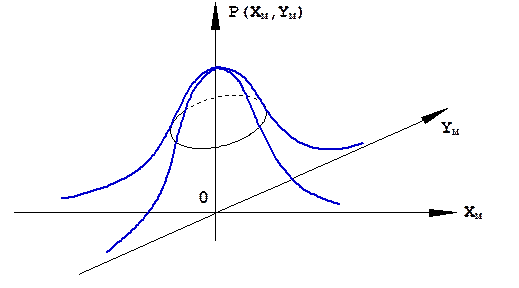
Рис.1.43. Совместное распределение квадратурных составляющих комплексной огибающей принятого сигнала.

Совместная плотность вероятности квадратурных составляющих представляется произведением одномерных нормальных (гауссовых) распределений вероятности каждой квадратурной составляющей

,

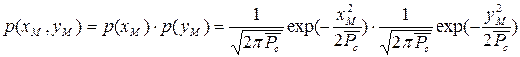что свидетельствует о независимости квадратурных составляющих для одного и того же момента времени.

Определение совместного распределения вероятности амплитуды и фазы принятого сигнала Е_с и φ_с связано с функциональным преобразованием

(М₁ , М₁^* ) → (Е_с , φ_с).

Поскольку 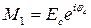, , 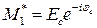якобиан этого преобразования равен

.

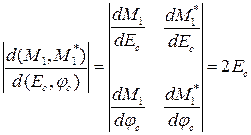Поэтому совместное распределение вероятности амплитуды и фазы принятого сигнала определяется выражением

.

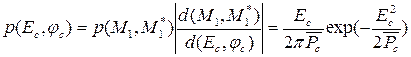Учитывая, что амплитуда принятого сигнала может принимать любые положительные значения, находим одномерное распределение фазы принятого сигнала:

,

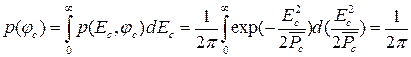которое является равномерным, на интервале -π до π радиан (рис.1.44).

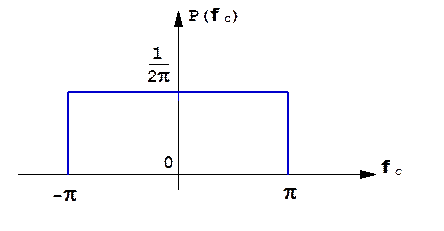
Рис.1.44. Равномерное распределение фазы принятого сигнала.

Учитывая, что фаза принятого сигнала может принимать любые значения от -π до π радиан, находим одномерное распределение вероятности амплитуды принятого сигнала

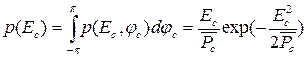, E_c ≥ 0,

которое называется релеевским распределением (рис.1.45).

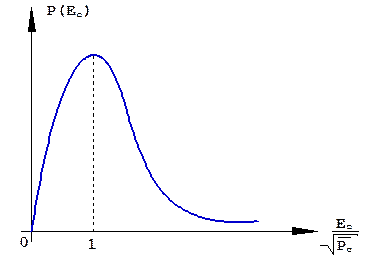
Рис.1.45.Релеевское распределение амплитуды принятого сигнала.

Совместная плотность вероятности амплитуды и фазы принятого сигнала есть произведение одномерных распределений вероятности амплитуды и фазы:

,

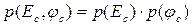что свидетельствует о независимости мгновенных значений амплитуды и фазы принятого сигнала для одного и того же момента времени.

Мгновенная мощность принятого сигнала есть половина квадрата его амплитуды:

.

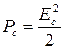Учитывая, что 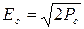, якобиан преобразования Е_с → Р_с равен

.

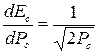Поэтому плотность вероятности мгновенной мощности принятого сигнала определяется выражением:

, P_c ≥ 0.

Такое распределение называется экспоненциальным (рис. 1.46).

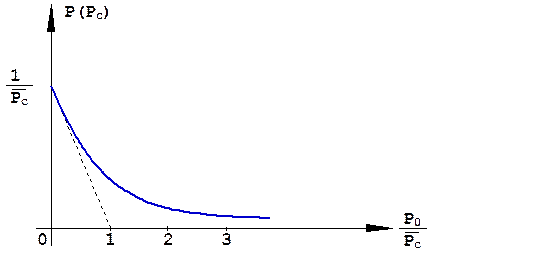
Рис.1.46. Экспоненциальное распределение мгновенной мощности принятого сигнала

Шумы и мешающие излучения

Решение всех задач РИС (обнаружение, распознавание-различение, измерение параметров сигнала) всегда затрудняется наличием помех искусственного или естественного происхождения. С точки зрения характера воздействия помех на РТС и принципов защиты РТС помехи целесообразно разделить на 3 группы; шумы, мешающие излучения и мешающие отражения. Как и сигналы, помехи являются электромагнитными полями и характеризуется пространственной, поляризационной и временной структурой. Однако, как и в случае с сигналами, отложим до поры - до времени рассмотрение пространственной и поляризационной структуры помех и сосредоточим внимание только на их временной структуре.

Внутренние шумы приемных устройств, а также внешние активные шумовые помехи, преднамеренно создаваемые для противодействия работе РТС, имеют подобные временные структуры и поэтому рассматриваются объединено. Шум (мешающие излучения) представляет собой нормальный случайный процесс с флуктуирующей амплитудой и фазой:

,

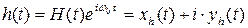где 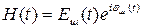- комплексная огибающая шума, x_h(t), y_h(t) - квадратурные составляющие шума.

Одна из квадратурных составляющих шума показана на рис. 1.47.

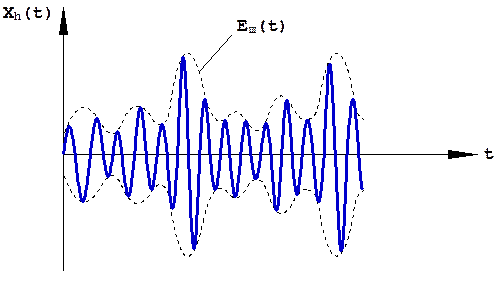
Рис. 1.47. Одна из квадратурных составляющих шума.

Корреляционная функция шума является результатом статистического усреднения

,

где 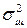- средняя мощность шума, r_ш(τ) - нормированная корреляционная функция шума.

Заметим, что средние значения шума, его комплексной огибающей и квадратурных составляющих равны нулю:

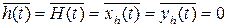
Нормированная корреляционная функция шума чаще всего аппроксимируется экспонентой (рис. 1.48):

,

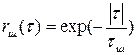где τ_ш - время корреляции шума.

Энергетический спектр шума

есть смещенный по частоте на величину несущей ω₀ энергетический спектр флуктуации шума:

.

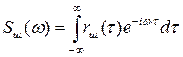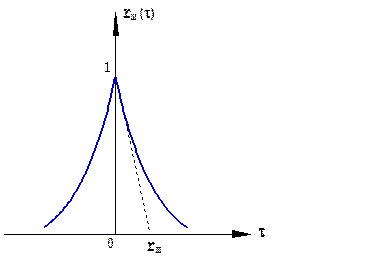
Рис. 1.48. Нормированная корреляционная функция шума.

При экспоненциальной корреляционной функции шума энергетический спектр флуктуации шума имеет форму резонансной кривой одиночного колебательного контура (рис. 1.49):

.

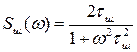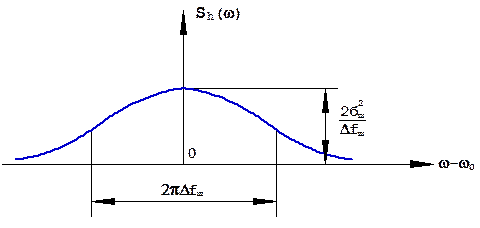
Рис. 1.49. Энергетический спектр шума.

Ширина спектра шума обратно пропорциональна удвоенному времени корреляции:

.

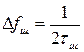Отношение средней мощности шума к ширине спектра называется спектральной плотностью шума:

.

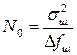Практически ширина спектра шума всегда превосходит ширину, спектра сигнала и полосу пропускания устройств обработки сигнала Δf_ш >> Δf₀ . Это означает, что в интересующем нас диапазоне частот можно пренебречь некоторым изменением энергетического спектра шума, считая его равномерным:

.

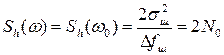Равномерный энергетический спектр является полезной математической идеализацией спектров. Случайный процесс с равномерным спектром называют белым шумом по аналогии с белым светом, имеющим сплошной и приблизительно равномерный спектр в пределах видимой его части (рис. 1.50).

Рис. 1.50. Энергетический спектр белого шума.

Корреляционная функция белого шума, являясь обратным преобразованием Фурье энергетического спектра, равна

,

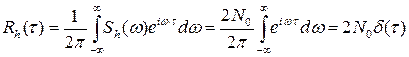т.е. представляет собой дельта-функцию, а нормированная корреляционная функция для белого шума (рис. 1.51):

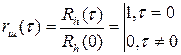
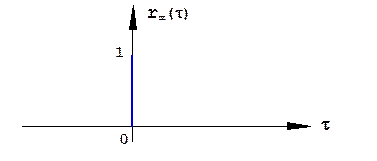
Рис. 1.51. Нормированная корреляционная функция белого шума.

Таким образом, белый шум характеризуется тем, что его значения в любые два сколь угодно близких момента времени некоррелированы.

Вероятностные характеристики шума описываются многомерной плотностью вероятности совокупности его дискретных значений, взятых с интервалом времени Δt >> τ_ш. При этом корреляционные свойства его дискретных значений описываются символом Кронекера δ_kl :

,

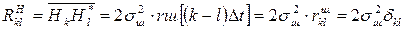где .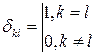

При этом определитель корреляционной матрицы шума и элементы обрат­ной корреляционной матрицы шума описываются следующими выражениями:

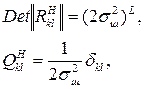
где L – число дискретных значений шума на некотором интервале наблюдения.

Многомерная плотность вероятности шума оказывается произведением соответствующих плотностей вероятности для различных дискретных значений шума:

,

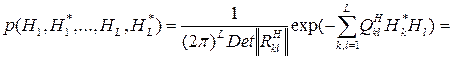
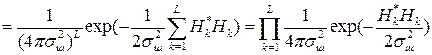что оказывается следствием независимости дискретных значений шума.

Одномерные распределения квадратурных составляющих, амплитуды, фазы и мгновенной мощности шума аналогичны соответствующим распределениям для принятого сигнала.