Квантовая нелокальность

Классические представления основаны на локальности объекта и отсутствии дальнодействия, когда характеристики объекта существуют до измерения, а взаимно удаленные измерительные приборы не влияют на изучаемый объект и на показания друг друга. Эйнштейн, Подольский и Розен в 1935 г. сформулировали парадокс ЭПР, который, как они считали, опровергает локальность теории и полноту описания явлений при помощи квантовой механики. Эксперименты с интерферометрами, проведенные в конце ХХ века, подтвердили выводы квантовой механики и поставили под сомнение принцип локальности.

Интерферометр – устройство, где проявляются волновые свойства объекта. Модификация конструкции интерферометра позволяет преобразовать поведение микрообъекта из волнового в корпускулярное и наоборот. Если это происходит в процессе движения объекта через интерферометр, то изменение поведения объекта называется задержанным выбором состояния в виде частицы или волны. Опыт теоретически разрабатывал Уилер с 1978 г. по 1983 г. Эксперимент с фотонами реализовал V. Jacques et al. в 2006 г. (Science 315, 966 (2007)), используя интерферометр Маха–Цендера. В 2015 г. подобный эсперимент выполнен с атомами гелия, он также подтвердил предсказания квантовой механики.

Джон Арчибальд Уилер (1911–2008)

В интерферометре Маха–Цендера, показанном на рис. 11, а, одиночный фотон направляется от источника S к делителю B1, который содержит полупрозрачное зеркало, напыленное на стеклянную пластинку. Фотонодержит полупрозрачное зеркало, показанное на рисунке проходит B1 в прямом направлении, или отражается вниз, с вероятностями 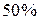и поступает в канал 1 или 2. Отразившись от зеркал M1 и M2, фотон проходит делитель B2, аналогичный B1, и регистрируется детектором D1 или D2. Делители расположены так, что обеспечивается одинаковый оптический путь фотона к детектору для каждого канала. Зеркала M1 и M2 сдвигают фазы в каждом канале на одинаковую величину, что не влияет на разность фаз и в формулах не учитывается.

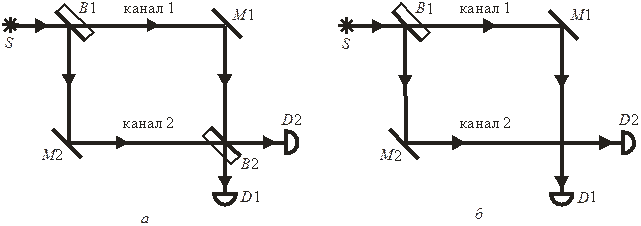
Рис. 11. Интерферометр Маха–Цендера

Из рис. 11, а получаем амплитуды вероятности прохождения фотона по двум каналам к детекторам:

D1: ,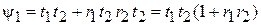

D2: ,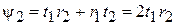

где

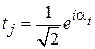– амплитуда прохождения делителя ;

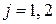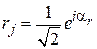– амплитуда отражения от делителя .

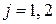При отражении теряется фаза 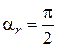, тогда 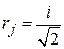. Получаем вероятности срабатывания детекторов

,

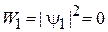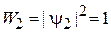. (3)

Следовательно, при прохождении фотона одновременно по двум каналам в виде волны срабатывает только детектор D2.

При убранном делителе B2 интерферометр показан на рис. 11, б. Фотон попадает к детектору D1, проходя по каналу 1, и к детектору D2, проходя по каналу 2. Из рис. 11, б получаем

,

,

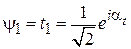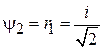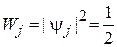. (4)

Рис. 11. Интерферометр Маха–Цендера

Следовательно, срабатывания детекторов равновероятны. Активизированный детектор указывает канал, по которому прошел фотон. Он распространяющаяся лишь по одному из возможных каналов, интерференция отсутствует. Фотон ведет себя как классическая локализованная частица. Удаление второго делителя превращает фотон в частицу.

В эксперименте с задержанным выбором V. Jacques et al. использовали интерферометр Маха–Цендера со световодами в каналах 1 и 2 протяженностью 48 м. Свет проходит это расстояние за 160 нс. Квантовый генератор случайных чисел меняет состояние делителя B2 – удаляет его из схемы, или подключает, за 40 нс. Два события – прохождение фотоном первого делителя и манипуляция со вторым делителем, разделены пространственно-подобным интервалом, что исключает возможность передачи информации о состоянии второго делителя к фотону, проходящему первый делитель. В рамках классической физики судьба фотона решается на первом делителе – он идет по одному каналу как частица, или одновременно по двум каналам как волна. Эксперимент подтвердил результаты квантовой механики (3) и (4), основанные на том, что все решается наличием или отсутствием второго делителя. Тогда в рамках классической физики возникает вопрос – как «узнает» фотон во что превратиться – в волну или частицу, если о подключении или удалении второго делителя можно узнать лишь после того, как фотон прошел первое разветвление каналов, где решается его судьба? Из изложенных особенностей квантового поведения следует, что до момента срабатывания детектора фотон остается суперпозицией волны и частицы. Как сказал Клышко – «фотон является фотоном (то есть локазизованной частицей), если это – зарегистрированный фотон». Для незарегистрированного фотона факт суперпозиции волны и частицы подтвердили последующие эксперименты, где второй делитель используется в квантовом режиме в виде суперпозиции состояний подключенного и отключенного элемента оптической схемы. Следовательно, незарегистрированный фотон не локализован в пространстве-времени, но присутствует во всех каналах одновременно и реагирует мгновенно на изменения в конструкции устройства, где бы эти изменения ни проводились. Такое поведение микрообъектаназываетсяквантовой нелокальностью, и это можно рассматривать как нахождение вне пространства-времени. Регистрация частицы локализует ее и переводит в пространство-время. Другие варианты объяснения проведенного эксперимента требуют нарушения постулата специальной теории относительности о невозможности перемещения со скоростью, превышающей скорость света, или нарушения принципа причинности о запрете опережающего сигнала. Использовать квантовую нелокальность для передачи информации со сверхсветовой скоростью невозможно из-за вероятностного характера квантовых процессов, отображающихся в пространстве-времени.