Квантова теорія теплоємності твердого тіла за Дебаєм

а). Фонони. Ідея Дебая полягає в тому, що найбільший внесок у теплоємність дають коливання низьких акустичних частот w із довжинами хвиль l, більшими від періоду d кристалічної решітки, причому d=(V/N)^1/3, де V- об'єм кристала з N частинками. Таким чином спектр теплових коливань обмежується деякою максимальною частотою 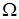. Тверде тіло можна розглядати як систему 3N частинок, зв’язаних пружною силою. Ці частинки здійснюють неперервні теплові коливання. Частинки мають 3N коливальних ступенів свободи. Цим ступеням свободи відповідають 3N узагальнених координат, які можна звести до 3N нормальних координат. Останні описують 3N гармонічних коливань частинок. Такі частинки називають ще осциляторами. З квантової механіки відомо, що енергія осцилятора має дискретні значення

E_n=(n+0,5)ћw, (n=0,1,2,3....). (7)

По аналогії з фотонним газом, кожному з таких акустичних коливань можна поставити у відповідність квазічастинку, яку називають фононом. Вони існують лише у межах кристала. Для них виконується закон збереження енергії. Квазіімпульс фонона 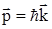, , 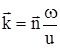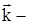хвильовий вектор, u - швидкість розповсюдження акустичної хвилі в напрямку 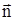, w - частота коливання осцилятора.При взаємодії фононів закон збереження імпульсу не виконується: імпульс може передаватися кристалічній решітці. Уведення фононів є зручним методом опису взаємодії акустичних хвильових процесів у кристалах.

Число квантових станів для фононів в об'ємі кристала V, де встановились акустичні коливання (стоячі хвилі) і фонони мають імпульс в інтервалі від p до p+dp дорівнює

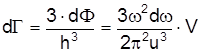, (8)

де 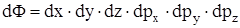- елемент фазового об'єму, 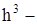фазовий об'єм, що приходиться на один дискретний стан коливань, h - стала Планка.

Фонони акустичного поля, породжені гармонічним осцилятором на частоті w, мають енергію

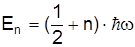, n=0,1,2,...

Внутрішню енергію поля фононів кристала для моля речовини (N=N_А) можна одержати у вигляді

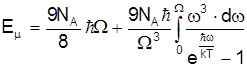. (9)

При високих температурах, коли теплова енергія значно більша енергії фонона kТ >> hw, в (5) можна вважати

.

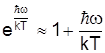При цьому інтеграл у (9) обчислюється так

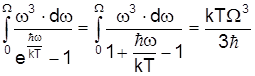
В цьому наближенні

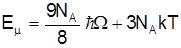. (10)

Диференціюючи (10) по Т отримаємо теплоємність, що відповідає правилу Дюлонга-Пті

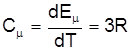. (11)

У випадку, коли енергія фонона більша від теплової енергії ћw > kT, теплоємність можна представити у вигляді

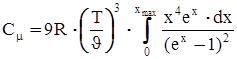, (12)

де

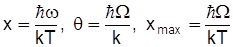
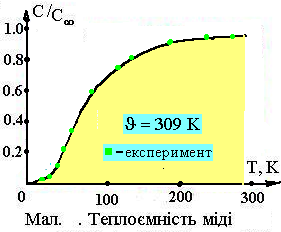
Величина q носить назву характеристичної функції Дебая і визначає граничну температуру кристала, нижче якої теплоємність потрібно розраховувати на основі квантування акустичного поля. У випадку низьких температур T <<q верхня границя інтегралу в (12) х_макс ® ¥, а сам інтеграл буде деяким числом. При цьому теплоємність буде пропорційна Т³ (див.Рис.3.), що узгоджується з експериментом. Досліди показують, що така залежність добре виконується для багатьох хімічно простих речовин.

[1] Нагадаємо, що теплота є мірою переданої чи отриманої енергії через границю двох контактуючих термодинамічних систем з різними температурами.

[MSOffice1]Величина n! = 1×2×3×...×n називається факторіалом числа n. Приведемо формулу Стірлінга для визначення n! для великих n: ln n!= n ln n - n + ln(2pn)/2