Відштовхуються, якщо напрямки струмів у них однакові 1 страница
Механіка
1. Що таке система відліку в механіці ?
1) Система координат та прилад для вимірювання часу.
2) Декартова система координат.
3) Набір синхронізованих годинників.
4) Полярна система координат.
5) Сукупність базисних векторів (ортів).
2. Що визначають формули r= ρ eρ+zez, v= (dρ/dt) eρ+ρ(dφ/dt)eφ
1) Радіус-вектори в полярній системі координат
2) Вектори швидкості в циліндричній системі координат.
3) Радіус-вектор у циліндричній системі і вектор швидкості в полярній.
4) Вектори швидкості в полярній системі координат.
5) Вектор швидкості і радіус-вектор у декартовій системі.
3. Що визначає формула
?
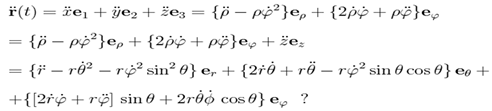1) Радіус-вектор матеріальної точки у різних системах координат.
2) Вектор швидкості матеріальної точки у різних системах координат.
3) Вектор прискорення в декартовій системі координат.
4) Вектор прискорення в полярній системі координат.
5) Вектор прискорення в декартовій, полярній, циліндричній і сферичній системах координат.
4. Які зв'язки визначають співвідношення
?
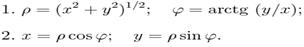1) Декартових і полярних координат матеріальної точки.
2) Декартових і циліндричних координат матеріальної точки.
3) Декартових і сферичних координат матеріальної точки.
4) Траєкторію матеріальної точки.
5) Рівняння еліпса.
5. Що вивчає кінематика?
1) Рух тіл без врахування сил, що діють на тіла.
2) Рух тіл під дією заданих сил.
3) Сили, що спричиняють рух.
4) Рух матеріальних точок.
5) Рух рідин і газів.
6. Що задають наступні формули?
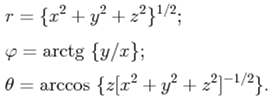
1)Рівняння руху матеріальної точки
2) Перехід від циліндричних до декартових координат
3) Перехід від сферичних до декартових координат
4) Перехід від декартових до сферичних координат
5) Перехід від декартових до полярних координат
6) Тригонометричні співвідношення.
7. Співвідношення
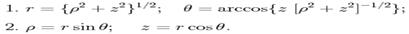
визначають:
1) Декартових і полярних координат матеріальної точки.
2) Декартових і циліндричних координат матеріальної точки.
3) Декартових і сферичних координат матеріальної точки.
4) Траєкторію матеріальної точки.
5) Циліндричних і сферичних координат матеріальної точки
8. Рівняння траєкторії матеріальної точки, кинутої під кутом α до горизонту,
у параметричній формі має наступний вигляд: 1)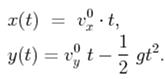 
------------------------------------------------------
2) 
------------------------------------------------------
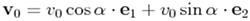
3) 
------------------------------------------------------
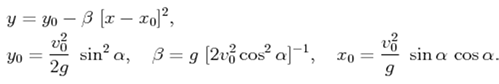
4) 
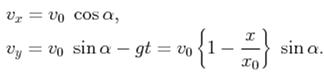
------------------------------------------------------ 5)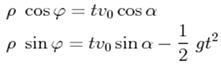 
------------------------------------------------------
9. У полярній системі координат рівняння руху матеріальної точки, кинутої під кутом α до
горизонту, має наступний вигляд: 1)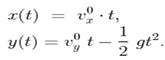 
------------------------------------------------------
2) 
------------------------------------------------------
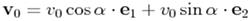
3) 
------------------------------------------------------
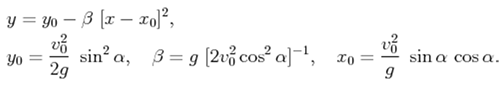
4) 
------------------------------------------------------
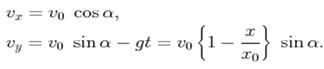
5) 
------------------------------------------------------
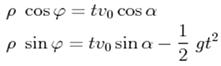
10. Рівняння траєкторії матеріальної точки, кинутої під кутом α до горизонту,
у явній формі має наступний вигляд: 1)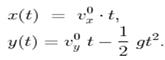 
------------------------------------------------------
2) 
------------------------------------------------------
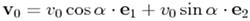
3) 
------------------------------------------------------
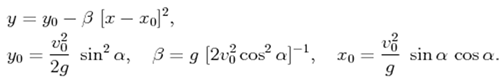
4) 
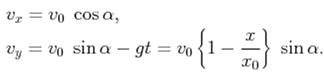
------------------------------------------------------ 5)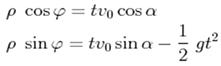 
------------------------------------------------------
11. Що таке фазовий простір в задачі про рух матеріальної точки ?
1) Тривимірний простір координат.
2) Тривимірний простір швидкостей.
3) Шестивимірний простір координат і швидкостей.
4) Двовимірний простір координат і швидкостей.
5) Чотиривимірний простір координат і швидкостей.
12. Вкажіть максимальне число збережуваних величин, що пов'язані з рухом матеріальної точки
1) Одна
2) Дві
3) Чотири
4) П'ять
5) Шість.
13. 
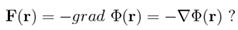Що описує формула
1) Зв'язок між силою і потенціальною енергією.
2) Рівняння руху матеріальної точки.
3) Рівняння рівноваги.
4) Напруженість електростатичного поля.
5) Зв'язок між силою і вектором швидкості.
14. 
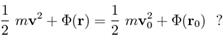Як називають рівність
1) Закон збереження енергії матеріальної точки.
2) Рівняння Бернуллі.
3) Рівняння руху.
4) Залежність маси матеріальної точки від швидкості.
5) Закон збереження швидкості.
15. 
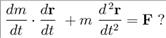Як називається і що описує рівняння
1) Другий закон Ньютона. Рух тіла змінної маси.
2) Рух тіла змінної маси під дією сили. Рівняння Мещерського.
3) Рівняння Бернуллі.
4) Рух тіла під дією зовнішньої сили при наявності тертя.
5) Рівняння Галілея.
16. 
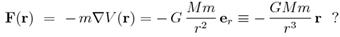Що описує формула
1) Рівняння еліпса.
2) Закон універсального тяжіння.
3) Рівняння руху.
4) Вектор сили, що діє на пробну частинку в полі гравітуючої маси.
5) Напруженість гравітаційного поля.
17. У формулі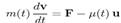 
величина µu називається:
1) Швидкістю втрати маси.
2) Зовнішньою силою.
3) Коефіцієнтом Мещерського.
4) Силою реакції (силою тяги).
5) Силою відтяжки.
18. Вираз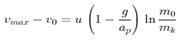 
називають:
1) Формулою різниць швидкостей.
2) Першою формулою Ціолковського.
3) Другою формулою Ціолковського.
4) Третьою формулою Ціолковського.
5) Формулою Кондратюка.
19. 
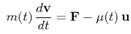Нехай у рівнянні величина F- результуюча гравітаційної сили та сили опору повітря, що діють на ракету. Чи описує це рівняння рух ракети, яка стартує з
поверхні Землі?
1) Так.
2) Ні. Це рівняння абсолютно неправильне.
3) Ні. Це рівняння описує рух ракети, що стартує з Марса.
4) Ні. Необхідно ще врахувати силу тиску газів, зумовлену різницею між тиском газу на зрізі сопла і зовнішнім тиском. Ця сила спричиняє додаткове прискорення ракети з висотою.
5) Ні. Необхідно ще врахувати силу тиску газів, зумовлену різницею між тиском газу з сопла і зовнішнім тиском. Ця сила спричиняє додаткове сповільнення ракети з висотою.
20. Оператор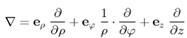 
є:
1) Оператором градієнта у циліндричній системі координат.
2) Оператором градієнта у сферичній системі координат.
3) Оператором градієнта у декартовій системі координат.
4) Оператором градієнта у полярній системі координат.
5) Оператором набла у довільній системі координат.
21. Виберіть правильні варіанти формул, які визначають точки повороту у випадку одновимірного руху частинки
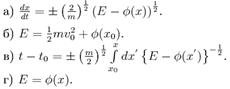
1) а).
2) б).
3) в).
4) г).
5) а) і г).
22. Який рух описує рівняння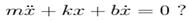 
1) Власні коливання гармонічного осцилятора.
2) Рух гармонічного осцилятора під дією тертя.
3) Вимушені коливання осцилятора.
4) Явище резонансу.
5) Рух супутника навколо Землі.
23. Що визначає формула
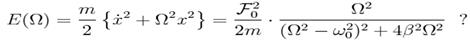
1) Енергію осцилятора під дією зовнішньої періодичної сили при наявності тертя.
2) Енергію гармонічного осцилятора.
3) Явище резонансу.
4) Енергію математичного маятника.
5) Енергію фізичного маятника.
24. 
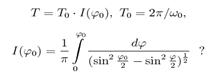Що визначає величина I(j0) у формулі
1) Залежність частоти коливань математичного маятника від амплітуди.
2) Залежність періоду коливань математичного маятника від часу.
3) Залежність періоду коливань математичного маятника від довжини нитки.
4) Залежність періоду коливань математичного маятника від власної частоти.
5) Залежність періоду коливань математичного маятника від амплітуди.
25. Фазова траєкторія гармонічного осцилятора є:
1) Параболою.
2) Гіперболою.
3) Довільною замкнутою кривою.
4) Еліпсом
5) Завжди колом.
26. Повна енергія гармонічного осцилятора є функцією:
1) Часу.
2) Амплітуди.
3) Часу і амплітуди.
4) Часу і початкової фази коливань.
5) Часу, амплітуди і початкової фази коливань.
27. 
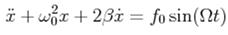Який рух описує рівняння ?
1) Власні коливання гармонічного осцилятора.
2) Рух гармонічного осцилятора під дією тертя.
3) Вимушені коливання осцилятора.
4) Явище резонансу.
5) Рух гармонічного осцилятора під дією зовнішньої періодичної вимушуючої сили та сил тертя.
28. Фізичний зміст логарифмічного декремента загасання:
1) Час, протягом якого амплітуда збільшується в е раз.
2) Час, протягом якого амплітуда зменшилася в 10 раз.
3) Час, протягом якого амплітуда зменшилася в 2.3 рази.
4) Час, протягом якого амплітуда зменшилася в 2 рази.
5) Логарифмічний декремент загасання є величина, обернена до числа періодів, за які амплітуда зменшується в е разів.
29. 
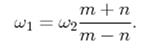Вираз описує:
1) Співвідношення між частотами коливань одного напряму, суперпозиція яких є періодичною функцією.
2) Співвідношення між частотами коливань одного напряму, суперпозиція яких не є періодичною функцією.
3) Співвідношення між періодами коливань одного напряму, суперпозиція яких не є періодичною функцією.
4) Співвідношення між періодами коливань одного напряму, суперпозиція яких є періодичною функцією.
5) Співвідношення між кутовими швидкостями різного радіуса.
30. Верхній з двох рисунків візуалізує двоямний потенціал. Що представляє нижній рисунок?
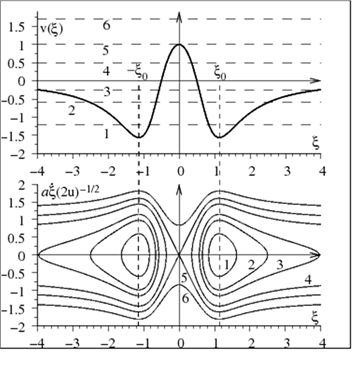
1) Потенціальну енергію матеріальної точки у полі з двоямним потенціалом.
2) Кінетичну енергію матеріальної точки у полі з двоямним потенціалом.
3) Сумарну енергію системи матеріальної точки у полі з двоямним потенціалом.
4) Фазовий портрет матеріальної точки у полі з двоямним потенціалом.
5) Траєкторію частинки у конфігураційному просторі в полі з двоямним потенціалом.
31. Вектори кутових швидкості та прискорення є:
1) Звичайними векторами.
2) Антипаралельними.
3) Аксіальними, тобто такими, напрям яких визначається правилом лівогвинтового свердлика.
4) Аксіальними, тобто такими, напрям яких визначається правилом правогвинтового свердлика.
5) Перпендикулярними до осі обертання матеріальної точки.
32. Що описують рівняння
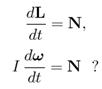
1) Обертальний рух матеріальної точки.
2) Поступальний рух матеріальної точки.
3) Суперпозицію поступального і обертального руху.
4) Рівномірний рух точки по колу.
5) Одновимірний рух.
33. У яких змінних зручніше описувати обертальний рух матеріальної точки?
1) У змінних m, v, P,...
2) У змінних I, ω, L,...
3) У будь-яких змінних.
4) У змінних m, v, L,...
5) У змінних I, v, L,...
34. При описі обертання матеріальної точки навколо осі величина її
моменту інерції є аналогічна:
1) Кінетичній енергії.
2) Силі.
3) Імпульсу.
4) Швидкості.
5) Масі.
35. При описі обертання матеріальної точки навколо осі величина її
кутової швидкості є аналогічна:
1) Кінетичній енергії.
2) Силі.
3) Імпульсу.
4) Швидкості.
5) Масі.
36. При описі обертання матеріальної точки навколо осі величина моменту
імпульсу є аналогічна:
1) Кінетичній енергії.
2) Силі.
3) Імпульсу.
4) Швидкості.
5) Масі.
37. Матеріальна точка буде мати нульовий момент сили при ненульових значеннях
її модулів вектора сили та радіус-вектора, якщо:
1) Вектори сили і радіус-вектора взаємно перпендикулярні.
2) Початки векторів сили і радіус-вектора не співпадають.
3) Вектори сили і радіус-вектора паралельні, або антипаралельні.
4) Кут між векторами сили і радіус-вектора складає 270 град.
5) Кут між векторами сили і радіус-вектора складає 130 град.
38. У випадку плоского руху фазовий простір має:
1) Один вимір.
2) Два виміри.
3) Три виміри.
4) Чотири виміри.
5) П'ять вимірів.
39. У випадку плоского руху кількість збережуваних величин рівна:
1) Одній.
2) Двом.
3) Трьом.
4) Чотирьом.
5) П'ятьом.
40. У формулі F= r/r*f(r) у загальному випадку величина f(r) є:
1) Довільною скалярною функцією модуля відстані від силового центра.
2) Спеціальною скалярною функцією модуля відстані від силового центра.
3) Густиною тіла,як функції r.
4) Законом всесвітнього тяжіння.
5) Законом Кулона.
41. 
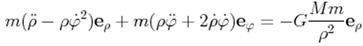Рівняння описує:
1) Векторне рівняння руху пробної частинки у полі центральних сил в циліндричній системі координат.
2) Скалярне рівняння руху пробної частинки у полі центральних сил в циліндричній системі координат.
3) Скалярне рівняння руху пробної частинки у полі центральних сил в полярній системі координат.
4) Векторне рівняння руху пробної частинки у полі центральних сил в полярній системі координат.
5) Векторне рівняння руху пробної частинки у полі центральних сил в сферичній системі координат.
42. Система рівнянь
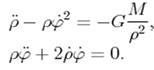описує:
1) Рух пробної частинки у полі центральних сил в циліндричній системі координат.
2) Припливні сили Місяця на поверхні Землі.
3) Рух пробної частинки у полі центральних сил в полярній системі координат.
4) Рух пробної частинки у полі центральних сил в сферичній системі координат.
5) Рух пробної частинки у полі центральних сил в декартовій системі координат.
43. Рівняння
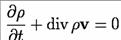
називається:
1) Рівнянням Нав'є-Стокса
2) Рівнянням збереження енергії
3) Рівнянням Ейлера (збереження імпульсу)
4) Рівнянням неперервності
5) Хвильовим рівнянням
44. Вираз
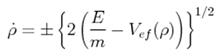, де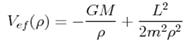 
є наслідком
інтегрування рівняння:
1) 
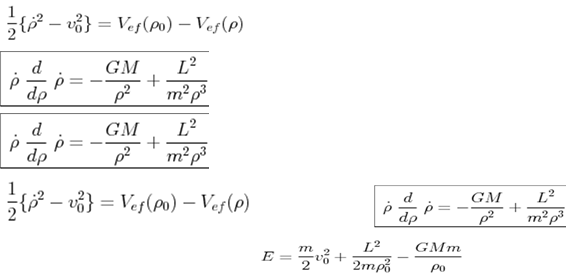з урахуванням,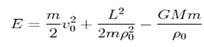 
2) з урахуванням, що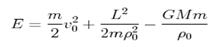 
3) з урахуванням, що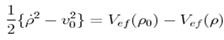 
4) з урахуванням, що
5) 
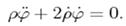з урахуванням, що
45. Що описує формула
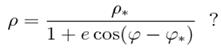
1) Траєкторію руху матеріальної точки у полі гравітуючої маси.
2) Рух по еліпсу.
3) Рух по гіперболі.
4) Рух по параболічній траєкторії.
5) Рух по кривій другого порядку, форма якої залежить від величини ексцентриситету.
46. Як називаються рівняння
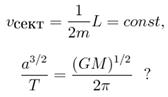
1) Рівняння Ньютона.
2) Другий і третій закони Кеплера.
3) Перший і другий закони Кеплера.
4) Перший і третій закони Кеплера.
5) Закони Галілея.
47. Назвіть нижче наведені величини і їх числові значення:
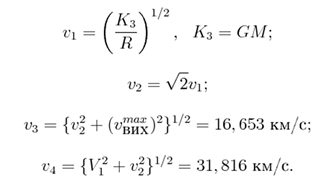
1) v1=7,910 км/с - перша космічна швидкість, v2=11,186 км/с - друга космічна швидкість, ..., v4 - четверта космічна швидкість.
2) v1=11,186 км/с - перша космічна швидкість, v2=7,910 км/с - друга космічна швидкість.
3)
|
|
вихзабезпечує вихід за межі гравітаційного поля Землі.
48. Яка з формул визначає радіус орбіти геостатичного супутника Землі?
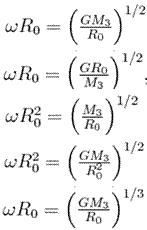1)
2)
3)
4)
5)
49. З рівняння
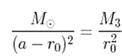
визначають:
1) Масу Землі.
2) Масу Сонця.
3) Радіус сфери притягання Землі відносно Сонця.
4) Радіус динамічної гравітаційної сфери впливу Землі.
5) Відстань від Землі до Сонця.
50. 
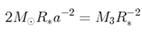З рівняння визначають:
1) Масу Землі.
2) Масу Сонця.
3) Радіус сфери притягання Землі відносно Сонця.
4) Радіус динамічної гравітаційної сфери впливу Землі.
5) Відстань від Землі до Сонця.
Заміна систем відліку.
51. Які з формул називаються перетвореннями Галілея?
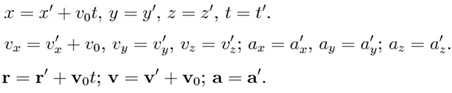1)
2)
3)
52. Що визначають формули
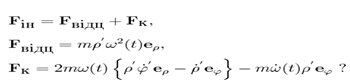
1) Силу інерції в обертовій системі відліку, записану в декартових координатах.
2) Силу Коріоліса.
3) Відцентрову силу.
4) Силу інерції в обертовій системі відліку, записану в полярних координатах.
5) Силу інерції, що діє на матеріальну точку, у системі відліку, яка обертається рівномірно навколо осі OZ.
53. Яка причина зміщення площини коливань маятника Фуко?
1) Опір повітря, наслідок несиметричної форми маятника.
2) Сила інерції.
3) Обертання Землі навколо осі.
4) Розтяг нитки маятника.
5) Прискорений рух маятника по траєкторії.
54. Навести приклади експериментальних підтверджень закону збереження
моменту імпульсу твердого тіла.
1) Крісло Жуковського, обертання балерини на пуантах, осьове обертання пульсарів.
2) Маятник Фуко.
3) Фізичний маятник.
4) Фізичний маятник, осьове обертання Землі.
5) Крісло Жуковського, математичний маятник.
55. 
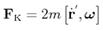Коли сила Коріоліса визначається за формулою ?
1) Завжди.
2) У випадку рівномірного обертання.
3) У випадку, коли матеріальна точка нерухома відносно неінерційної системи відліку.
4) Тільки у випадку польоту з Заходу на Схід.
5) Тільки у випадку польоту зі Сходу на Захід.
56. Коли сила Коріоліса визначається за формулою FK= m[r',dω/dt] ?
57. Завжди.
2) У випадку рівномірного обертання.
3) У випадку, коли матеріальна точка нерухома відносно неінерційної системи відліку.
4) Тільки у випадку польоту з Заходу на Схід.
5) Тільки у випадку польоту зі Сходу на Захід.
58. На рисунку показано:
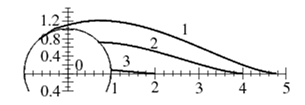
1) Екваторіальні траєкторії падіння до граничної висоти, вище якої предмети ставатимуть штучними супутниками Землі.
2) Екваторіальні траєкторії падіння до граничної висоти, вище якої предмети ставатимуть штучними супутниками Землі у випадку, якщо Земля була б не рухома.
3) Траєкторії ракети, яка стартує з поверхні Місяця.
4) Полум'я свічки.
5) Комету з хвостом.
59. На рисунку показано:
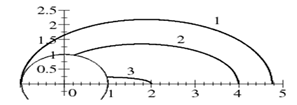
1) Екваторіальні траєкторії падіння до граничної висоти, вище якої предмети ставатимуть штучними супутниками Землі.
2) Екваторіальні траєкторії падіння до граничної висоти, вище якої предмети ставатимуть штучними супутниками Землі у випадку, якщо Земля була б не рухома.
3) Траєкторії ракети, яка стартує з поверхні Місяця.
4) Полум'я свічки.
5) Комету з хвостом.
60. Чи описує дана система рівнянь рух маятника Фуко?
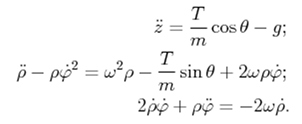
1) Так, ця система рівнянь описує рух маятника Фуко, де б він не знаходився.
2) Так, ця система рівнянь описує рух маятника Фуко, але тільки у випадку, якщо він закріплений на полюсі Землі.
3) Ні. Це взагалі неправильна система рівнянь.
4) Ні. Ця система рівнянь не підходить для маятника Фуко.
5) Ні. Ця система рівнянь описує зовсім інший процес.
61. 
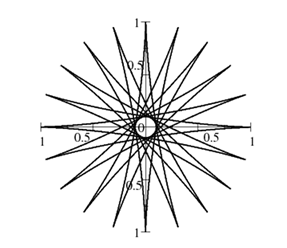На рисунку показано:
1) Вигляд відносно земного спостерігача траєкторії маятника Фуко, запущеного з наступними початковими умовами: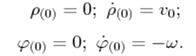 
2) Вигляд траєкторії маятника Фуко, відносно земного спостерігача з наступними
початковими умовами: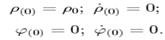 
3) Вигляд траєкторії маятника Фуко, відносно віддаленого від Землі спостерігача.
4) Вигляд траєкторії маятника Фуко, відносно спостерігача, що знаходиться у системі координат, яка рухається навколо Сонця, синхронно з Землею, ближче до Сонця.
5) Вигляд траєкторії маятника Фуко, відносно спостерігача, що знаходиться у системі координат, яка рухається навколо Сонця, синхронно з Землею, дальше від Сонця.
62. Які з перевотворень називають перетвореннями Лоренца?
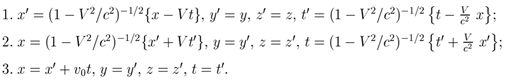
1) 1
2) 2
3) 1 та 2
4) 3
5) 1 та 3
63. Які з формул є наслідком перетворень Лоренца?
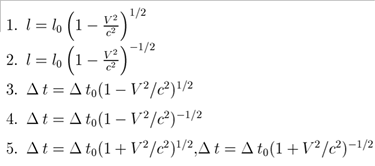
1) 2 та 3
2) 3
3) 1 та 4
4) 2
5) 5
64. Як називаються співвідношення
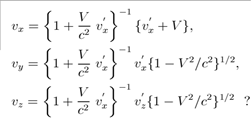
1) Правило додавання швидкостей у механіці Ньютона
2) Правило додавання швидкостей у спеціальній теорії відносності
3) Правило додавання швидкостей у механіці Галілея
4) Проекції вектора швидкості фотона
5) Правило додавання швидкостей у неінерційних системах відліку
65. Які з наведених формул визначають енергію та імпульс релятивістської частинки?
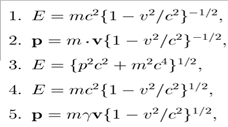
1) 3
2) 1,2,3
3) 4,5
4) 5
5) 2,5
66. У матриці, наведеній нижче, величина Г дорівнює:
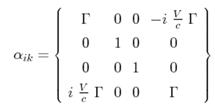
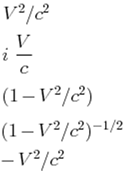1)