Молекулярная физика и термодинамика
Методические указания по решению задач
Омск 2004
Составители:
Ласица Александр Михайлович;
Кондратьева Тамара Николаевна;
Павловская Ольга Юрьевна.
Печатается по решению редакционно-издательского совета Омского государственного технического университета.
Молекулярная физика и термодинамика – разделы физики, в которых изучаются макроскопические процессы, связанные с огромным числом содержащихся в телах атомов и молекул. Для исследования этих процессов применяются два качественно различных метода: статистический и термодинамический. Первый лежит в основе молекулярной физики, второй – термодинамики.
Основные положения молекулярной физики
Молекулярная физика – раздел физики, изучающий строение и свойства вещества, исходя из молекулярно–кинетических представлений, основывающихся на том, что все тела состоят из молекул, находящихся в непрерывном движении.
Наиболее полное описание любой системы состояло бы в определении уравнений движения всех тел, входящих в нее, однако из-за большого числа частиц входящих в макроскопическую систему, данная задача является принципиально неразрешимой. Состояние системы в молекулярной физике определяется небольшим набором величин, называемых параметрами состояния (термодинамическими параметрами) характеризующих свойства системы в целом. В качестве основных параметров состояния выбирают температуру Т, давление р и объем V. Если система находится во внешнем поле, то к параметрам состояния добавляются характеристики поля.
Параметры состояния в большинстве случаев не являются независимыми, они связаны между собой некоторым уравнением, называемым уравнением состояния. Одной из основных задач молекулярной физики является установление явного вида уравнения состояния и установление связи между параметрами состояния и усредненными характеристиками движения частиц, входящих в систему. Для решения такой задачи приходится прибегать к рассмотрению различных физических моделей вещества. Одной из самых простых моделей является модель идеального газа.
Идеальным называют газ, удовлетворяющий следующим условиям:
1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда;
2) потенциальной энергией взаимодействия молекул можно пренебречь;
3) столкновения молекул между собой и со стенками сосуда абсолютно упругие.
Модель идеального газа можно использовать при изучении реальных газов, так как в условиях, близких к нормальным, а также при низких давлениях и высоких температурах они близки к идеальному газу. Кроме того, внеся поправки на собственный размер молекул и действующие молекулярные силы, можно перейти к теории реальных газов.
Уравнение состояния идеального газа носит название уравнение Менделеева -Клапейрона и имеет вид
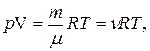
где n=m/m-число молей газа, R=8,31 Дж/(моль×К)-универсальная газовая постоянная. Данное уравнение является обобщением установленных экспериментально законов поведения идеального газа к которым относятся законы:
1) Бойля-Мариотта: pV = const при Т, m = const;
2) Шарля: 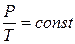 при V, m=const;
при V, m=const;
3) Гей-Люссака: 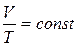 при P, m=const;
при P, m=const;
4) Дальтона - давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов:
p = p1 + p2 + p3 +¼,
(р1, р2,…- парциальные давления – давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре);
5) Авогадро - моли любых газов при одинаковых температуре и давлении занимают одинаковые объемы (при нормальных условиях p = 1,013×105 Па, Т = 273,15 К, для одного моля этот объем V = 22,41×10-3 м3).
По определению, в одном моле различных веществ содержится одно и то же число молекул, называемое постоянной Авогадро: NA = 6,022×1023 моль-1.
Уравнение Менделеева - Клапейрона может быть переписано в другом виде:
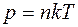 ,
,
где n – концентрация молекул газа, 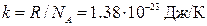 – постоянная Больцмана.
– постоянная Больцмана.
Основным уравнением молекулярно кинетической теории идеального газа называется уравнение связывающее давление, оказываемое идеальным газом на стенки сосуда с характеристиками его молекул:
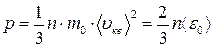
(m0 – масса молекулы газа; 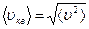 - средняя квадратичная скорость молекул,
- средняя квадратичная скорость молекул, 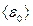 -средняя кинетическая энергия поступательного движения одной молекулы). Принимая во внимание уравнение Менделеева–Клапейрона, получаем
-средняя кинетическая энергия поступательного движения одной молекулы). Принимая во внимание уравнение Менделеева–Клапейрона, получаем
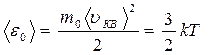 .
.
Средняя кинетическая энергия поступательного движения одной молекулы идеального газа пропорциональна термодинамической температуре и зависит только от нее.
Более детальное описание системы заключается в определении не только средней скорости, но и закона распределения молекул по скоростям. Этот закон теоретически выведен Максвеллом. Закон Максвелла описывается некоторой функцией f(u), называемой функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, то на каждый интервал скорости будет приходиться некоторое число молекул dN(u), имеющих скорости в интервале от u до u+du , пропорциональное ширине интервала du.
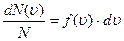 и
и 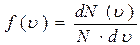 , где N – число молекул газа.
, где N – число молекул газа.
Таким образом, функция f(u) определяет относительное число молекул 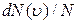 , скорости которых лежат в интервале от u до u+du. Можно также сказать, что функция f(u) определяет вероятность попадания скорости молекулы в интервал от u до u+du.
, скорости которых лежат в интервале от u до u+du. Можно также сказать, что функция f(u) определяет вероятность попадания скорости молекулы в интервал от u до u+du.
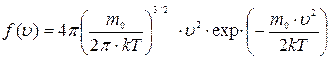 .
.
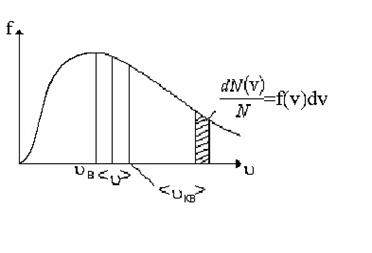 График функции представляет собой немонотонную кривую обращающуюся в ноль при u = 0 и u = ¥. При увеличении температуры максимум функции распределения становится более пологим и смещается в область больших скоростей. Скорость при которой достигается максимум функции распределения называется наиболее вероятной скоростью uВ. Этой скоростью и близкой к ней обладает наибольшее число молекул. Кривая несимметрична относительно uВ. Расчеты показывают, что
График функции представляет собой немонотонную кривую обращающуюся в ноль при u = 0 и u = ¥. При увеличении температуры максимум функции распределения становится более пологим и смещается в область больших скоростей. Скорость при которой достигается максимум функции распределения называется наиболее вероятной скоростью uВ. Этой скоростью и близкой к ней обладает наибольшее число молекул. Кривая несимметрична относительно uВ. Расчеты показывают, что
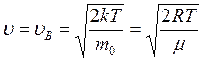 .
.
С помощью функции распределения можно установить среднее значение любой величины X зависящей от скорости
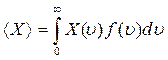
Например, среднее значение скорости
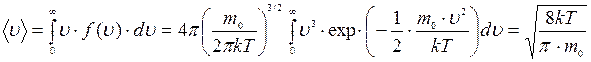 ,
,
среднее значение квадрата скорости
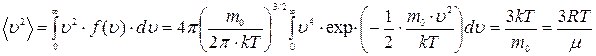 .
.
Если газ находится в поле внешних сил, то кроме распределения по скоростям устанавливается распределение по координатам. В случае поля тяготения Земли это приводит к тому, что концентрация молекул и давление газа изменяются с высотой. Закон изменения установлен Больцманом для изотермической атмосферы:
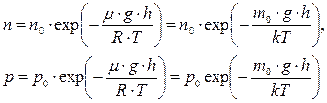
где p0 и n0-давление и концентрация молекул на высоте h = 0. Первая из формул называется распределением Больцмана, вторая - барометрической формулой.
Молекулы газа, находясь в состоянии хаотического движения, непрерывно сталкиваются друг с другом. Между двумя последовательными столкновениями молекулы проходят некоторый путь l, который называется длиной свободного пробега. В общем случае длина пути между последовательными столкновениями различна, поэтому можно говорить о средней длине свободного пробега молекул < l>. За единицу времени молекула проходит путь, равный <u> и, если <z> - среднее число столкновений за единицу времени, то 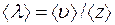 .Расчеты показывают, что
.Расчеты показывают, что
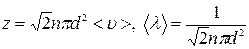
(d - эффективный диаметр молекулы).
В термодинамически неравновесных системах возникают особые необратимые процессы, называемые явлениями переноса, в результате которых происходит пространственный перенос энергии (теплопроводность), массы (диффузия), импульса (внутреннее трение). Уравнения, описывающие явления переноса называются:
1. законом теплопроводности Фурье:
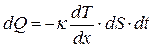
( 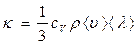 - коэффициент теплопроводности, сV - удельная теплоемкость при постоянном объеме),
- коэффициент теплопроводности, сV - удельная теплоемкость при постоянном объеме),
2. законом диффузии Фика:
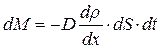
( 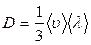 - коэффициент диффузии),
- коэффициент диффузии),
3. законом внутреннего трения Ньютона:
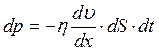
( 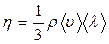 - коэффициент внутреннего трения (вязкость)).
- коэффициент внутреннего трения (вязкость)).
Знак минус в уравнениях показывает, что перенос энергии, массы и импульса идет в направлении противоположном направлению возрастания температуры, плотности и скорости соответственно. Коэффициенты k, D и h связаны простыми соотношениями:
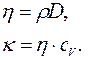
Примеры решения задач
Задача № 1
В сосуде объёмом V = 1 л находится углекислый газ массой m = 0,2 г. При температуре T =2600 K некоторая часть молекул диссоциировала на молекулы кислорода и окиси углерода. При этом давление газа в сосуде оказалось равным 108 кПа. Определить какая часть молекул диссоциировала.
| Дано: V = 1 л m = 0,2 г Т=2600 К Р=108 кПа |
| α -? |
Решение:
Рассмотрим уравнение диссоциации углекислого газа
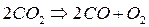
Таким образом, каждый моль углекислого газа, распадаясь вызывает появление одного моля окисла углерода и половину моля кислорода. В результате распада части молекул в сосуде будут находиться три газа: CO2, CO, O2. По закону Дальтона найдём выражение для давления, создаваемого данной смесью газов
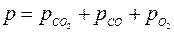 .
.
Введём степень диссоциации 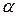 - отношение числа молей распавшихся молекул к начальному числу молей вещества
- отношение числа молей распавшихся молекул к начальному числу молей вещества 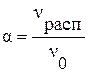 . Тогда число молей CO2
. Тогда число молей CO2
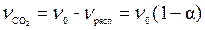 ,
,
число молей CO 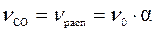 ,
,
число молей O2 (с учётом уравнения реакции) 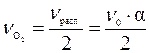 .
.
 Из уравнения Менделеева–Клапейрона
Из уравнения Менделеева–Клапейрона
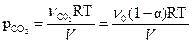 ,
, 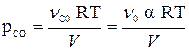 ,
, 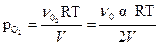 .
.
Общее давление будет связано со степенью диссоциации 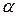 уравнением
уравнением
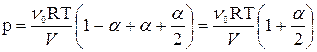 .
.
Так как 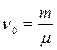 (m = 44·10-3 кг/моль – молярная масса CO2) , то
(m = 44·10-3 кг/моль – молярная масса CO2) , то 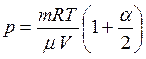 . Выражая
. Выражая 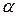 и производя расчет, получим
и производя расчет, получим 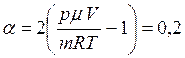 .
.
Ответ: степень диссоциации газа a = 0,2.
Задача № 2
Используя функцию распределения Максвелла по скоростям, найдите наиболее вероятное значение кинетической энергии атомов гелия, который при давлении P = 105 Па имеет плотность r=160 г/м3.
Дано: p = 105 Па 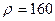 г/м3 г/м3 |
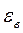 -? -? |
Решение:
Запишем функцию распределения Максвелла по скоростям.
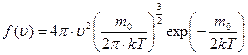 .
.
Поскольку нужно найти наиболее вероятное значение энергии, имеет смысл перейти от распределения по скоростям к распределению по энергиям f( 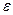 ). По смыслу функции распределения относительное число молекул скорости которых лежат в интервале скоростей
). По смыслу функции распределения относительное число молекул скорости которых лежат в интервале скоростей 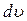 , которому соответствует интервал энергий
, которому соответствует интервал энергий 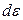 , равно
, равно
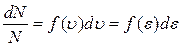 .
.
Из данного выражения можно получить соотношение связывающее две функции распределения: 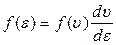 . Из формулы видно: для перехода от распределения по скоростям к распределению по энергиям недостаточно просто выразить скорость через энергию. Поскольку
. Из формулы видно: для перехода от распределения по скоростям к распределению по энергиям недостаточно просто выразить скорость через энергию. Поскольку 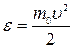 ,
, 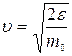 , то производная
, то производная 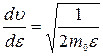 , и выражения для распределения по энергиям будет иметь вид.
, и выражения для распределения по энергиям будет иметь вид.
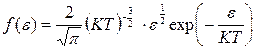 .
.
Наиболее вероятное значение энергии 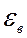 соответствует максимуму функции распределения. Соответственно производная
соответствует максимуму функции распределения. Соответственно производная 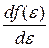 должна быть равна нулю:
должна быть равна нулю:
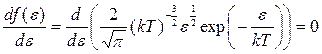 ,
,
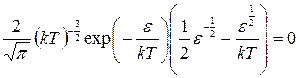 ,
,
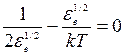 ,
, 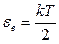 .
.
Обращаем внимание, что выражение для наиболее вероятной энергии нельзя получить подставив в формулу 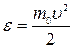 выражения для наиболее вероятной скорости
выражения для наиболее вероятной скорости 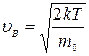 (в этом случае получилось бы
(в этом случае получилось бы 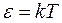 ).
).
Из уравнения Менделеева-Клапейрона следует, что 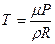 , значит
, значит
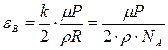
(в последней формуле учтено, что R = NA·k). Подставляя данные из условия и молярную массу гелия 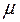 = 4·10-3 кг/моль, получим
= 4·10-3 кг/моль, получим 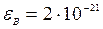 Дж.
Дж.
Ответ: наиболее вероятное значение кинетической энергии атома гелия 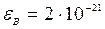 Дж.
Дж.
Задача № 3
Ротор центрифуги, заполненный радоном, вращается с частотой 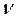 = 50 Гц. Радиус ротора a = 0,5 м. Определить давление газа на стенку ротора, если в его центре давление p0 = 105 Па. Температуру по всему объёму считать постоянной, равной Т=300 К.
= 50 Гц. Радиус ротора a = 0,5 м. Определить давление газа на стенку ротора, если в его центре давление p0 = 105 Па. Температуру по всему объёму считать постоянной, равной Т=300 К.
Дано: 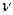 = 50 Гц a = 0,5 м. p0= 105 Па. Т=300 К. = 50 Гц a = 0,5 м. p0= 105 Па. Т=300 К. |
| p -? |
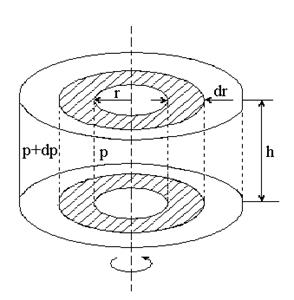 Решение:
Решение:
Рассмотрим находящийся в центрифуге цилиндрический слой воздуха бесконечно малой толщины dr, такой, что можно считать, что все молекулы данного слоя находятся на одинаковом расстоянии r от оси вращения.
Запишем для данного слоя второй закон Ньютона :
F = ma
Под силой F в данном случае нужно понимать разность сил давления действующих с внешней и внутренней стороны слоя
F = ((p+dp)-p)2 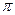 r h = dp 2
r h = dp 2 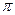 r h,
r h,
где произведение 2 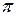 r h даёт площадь боковой поверхности слоя воздуха. Массу данного слоя можно получить, умножив плотность воздуха r на объём слоя dV = 2
r h даёт площадь боковой поверхности слоя воздуха. Массу данного слоя можно получить, умножив плотность воздуха r на объём слоя dV = 2 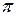 r dr h; m =
r dr h; m = 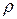 dV =
dV = 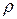 2
2 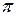 r dr h. Все молекулы данного слоя вовлечены во вращательные движения с угловой скоростью
r dr h. Все молекулы данного слоя вовлечены во вращательные движения с угловой скоростью 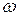 и находятся на одинаковом расстоянии r от оси вращения, следовательно, обладают одинаковым нормальным ускорением
и находятся на одинаковом расстоянии r от оси вращения, следовательно, обладают одинаковым нормальным ускорением 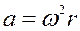 . Объединяя выражения, получим
. Объединяя выражения, получим
dp = 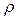 dr·
dr· 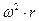
(в правой и левой части сокращён одинаковый множитель 2 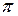 r h). Из уравнения Менделеева–Клапейрона следует
r h). Из уравнения Менделеева–Клапейрона следует 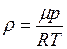 . Подставляя в предыдущее выражение и разделяя переменные, получим
. Подставляя в предыдущее выражение и разделяя переменные, получим 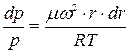 .
.
Проинтегрируем полученное уравнение:
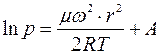
где А - некоторая постоянная интегрирования. Представим её в виде натурального логарифма от некоторой другой постоянной С:A = ln C. Тогда
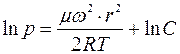
или 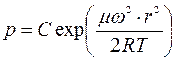 .
.
По условию задачи на оси центрифуги давление должно быть p0, это возможно только в случае, когда C= p0. Заменяя C на p0, определим давление как функцию расстояния до оси вращения:
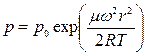 .
.
Вспоминая, что 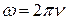 , получим расчетную формулу для давления
, получим расчетную формулу для давления
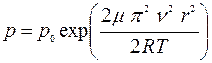 .
.
Подставляя в последнюю формулу r = a = 0,5 м и молярную массу радона
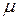 = 0,222 кг/моль, вычислим давление газа на стенку центрифуги p = 3 ×105 Па.
= 0,222 кг/моль, вычислим давление газа на стенку центрифуги p = 3 ×105 Па.
Ответ: давление на стенку ротора p0 =3 ×105 Па.
Задача № 4
Стальной стержень длиной ℓ = 20 см с площадью поперечного сечения S = 3 см2 нагревается с одного конца до температуры t1 = 3000С, а другим концом упирается в лёд. Предполагая, что передача тепла происходит исключительно вдоль стержня (без потерь через стенки), подсчитать массу льда, растаявшего за время t = 10 мин. Теплопроводность стали k = 60 Вт/(м∙К).
Дано: t1 = 3000С S = 3см2 t2 = 00С ℓ = 20см. 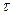 = 10мин. k= 60 Вт/м∙К = 10мин. k= 60 Вт/м∙К |
| m -? |
Решение:
Найдём количество теплоты полученное льдом. Для этого запишем уравнение теплопроводности.
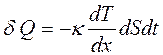 .
.
Считая, что поток тепла не изменяется со временем и постоянен в пределах сечения стержня, данную формулу можно записать в виде
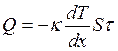 .
.
Производная 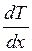 представляет собой градиент температуры в стержне. Так как длина стержня равна ℓ, а разность температур на его концах t1-t2, можно произвести замену
представляет собой градиент температуры в стержне. Так как длина стержня равна ℓ, а разность температур на его концах t1-t2, можно произвести замену 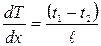 . Знак минус в выражении Q можно не учитывать, так как он показывает, что направление переноса теплоты противоположно направлению возрастания температуры. С учётом этого количество теплоты получённое льдом:
. Знак минус в выражении Q можно не учитывать, так как он показывает, что направление переноса теплоты противоположно направлению возрастания температуры. С учётом этого количество теплоты получённое льдом:
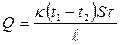 .
.
Так как всё это количество теплоты идёт на плавление льда, Q = mb (b = 3,3×105 Дж/кг – удельная теплота плавления льда). Объединяя выражения и производя расчеты получим 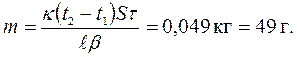
Ответ: масса растаявшего льда m = 0,049 кг = 49 г.
Задача № 5
В результате некоторого процесса вязкость некоторого идеального газа увеличилась в 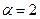 раза, а коэффициент диффузии – в
раза, а коэффициент диффузии – в 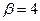 раза. Во сколько раз увеличилось давление газа.
раза. Во сколько раз увеличилось давление газа.
Дано: 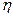 = = 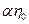 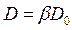 |
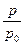 -? -? |
Решение:
Согласно молекулярно кинетической теории,
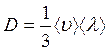 ,
, 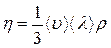 ,
,
где 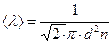 - средняя длина свободного пробега,
- средняя длина свободного пробега, 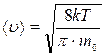 - средняя скорость движения молекул, r=m0n- плотность газа.
- средняя скорость движения молекул, r=m0n- плотность газа.
По основному уравнению МКТ 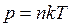 , поэтому
, поэтому 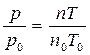 . Подставим в выражение для h значения
. Подставим в выражение для h значения 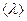 ,
, 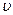 и r, тогда
и r, тогда

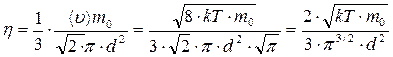 ;
;
Из формул видно, что 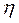 ~
~ 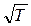 , значит,
, значит, 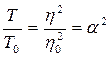 . Для того чтобы найти отношение
. Для того чтобы найти отношение 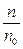 , свяжем между собой
, свяжем между собой 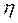 и D. Из формул видно, что
и D. Из формул видно, что  . Отсюда
. Отсюда 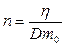 , а отношение
, а отношение 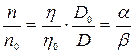 . В итоге получаем отношение давлений
. В итоге получаем отношение давлений 
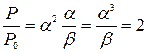 .
.
Ответ: давление возрастет в два раза.
Задачи, рекомендуемые для аудиторных занятий
1. 12 г газа занимают объем 4 дм3 при температуре 70С. После нагревания газа при постоянном давлении его плотность стала равна 0,6 мг/см3. До какой температуры нагрели газ?
Ответ: до 1400 К.
2. В сосуде находится 14 г азота и 9 г водорода при температуре 100С и давлении 1 МПа. Найти молярную массу смеси и объем сосуда.
Ответ: 4,6 г/моль; 12 дм3.
3. В двух сосудах емкостями 3 и 4 л находится газ под давлениями 0,2 и 0,1 МПа соответственно. Температура в обоих сосудах одинакова. Под каким давлением будет находиться газ, если соединить сосуды трубкой?
Ответ: 140 кПа.
4. В баллоне емкостью 150 см3 содержится газ при температуре 30 0С. Вследствие утечки из колбы вышло 4∙1018 молекул. Определить, на сколько понизилось при этом давление газа?
Ответ: 112 Па.
5. Плотность некоторого газа равна 6∙10-2 кг/м3, средняя квадратичная скорость молекул этого газа равна 500 м/с. Найти давление, которое газ оказывает на стенки сосуда.
Ответ: 5 кПа.
6. В баллоне емкостью 5 л находится 25∙1021 молекул азота. Найти среднюю квадратичную скорость его молекул, если давление в баллоне P = 720 мм рт.ст.
Ответ: 1100 м/с.
7. Найти число молекул азота в 1 см3 при нормальных условиях и обладающих скоростью: а) между 99 м/с и 101 м/с; б) между 499 м/с и 501 м/с.
Ответ: 8,6∙1018; 4,9∙1019.
8. Найти для газообразного азота температуру, при которой скоростям молекул υ1 = 300 и υ2 = 600 м/с соответствуют одинаковые значения функции распределения Максвелла.
Ответ: 330 К.
9. Полагая температуру воздуха и ускорение свободного падения не зависящими от высоты, определить, на какой высоте h над уровнем моря плотность воздуха меньше своего значения на уровне моря в 2 раза. Температура воздуха t = 00С.
Ответ: 5,5 км.
10. Вычислить среднюю длину свободного пробега молекул воздуха при температуре 17 0С и нормальном давлении. Эффективный диаметр молекул воздуха принять равным 3∙10-8 см.
Ответ: 10-7 м.
11. Определить среднее число всех столкновений между молекулами, которые происходят в течение 1 с в 1 см3 кислорода при температуре 17 0С и давлении 5 мм рт. ст. Эффективный диаметр молекулы кислорода 2,9∙10-8 см.
Ответ: 2,27∙1024.
12. Найти среднюю длину свободного пробега азота, если его динамическая вязкость 17 мкПа×с, d = 0,3 нм.
Ответ: 0,09 нм.
13. Найти коэффициент теплопроводности воздуха при температуре 10 0С и давлении 100 кПа, если диаметр молекулы воздуха принять равным 0,3 нм.
Ответ: 13 мВт/(мּК).
14. Вычислить коэффициент диффузии и динамическую вязкость азота при давлении 0,1 МПа и температуре 7 0С.
Ответ:14ּ10-6 м2/с и 17ּ10-6 Паּс.
Задачи для самостоятельного решения
1. Сколько молекул содержится в 2 л кислорода, находившегося при температуре 170С и давлении 0,2 МПа?
2. Сосуд емкостью 1 л содержит 1,5 г некоторого газа под давлением 0,25 МПа. Определить среднюю квадратичную скорость молекул газа.
3. Среднеквадратичная скорость молекул газа при давлении 0,1 МПа составляет 500 м/с. Определить плотность газа при этих условиях.
4. При какой температуре средняя квадратичная скорость атомов гелия станет равной второй космической скорости (11,2 км/с)?
5. Определить массу одной молекулы углекислого газа.
6. В сосуде емкостью 5 л находится 0,2 моля некоторого газа. Определить, какой это газ, если его плотность 1,12 кг/м3.
7. Газ при температуре 309 К и давлении 0,7 МПа имеет плотность 12 кг/м3. Определить молярную массу этого газа.
8. Сколько молекул газа содержится в баллоне вместимостью 30 л при температуре 300 К и давлении 5 МПа?
9. Плотность некоторого газа 0,06 кг/м3, средняя квадратичная скорость молекул этого газа 500 м/с. Найти давление, которое газ оказывает на стенки сосуда.
10. Давление газа 1 МПа; концентрация молекул 1010 см-1. Найти температуру газа и среднюю кинетическую энергию поступательного движения одной молекулы.
11. Плотность воздуха при температуре 0 0С и давлении 760 мм рт. ст. равна 0,001293 г/см3. Сколько весит литр воздуха при температуре 27,3 0С и давлении 750 мм рт. ст.?
12. Баллон содержит газ при t1 = 500С и давлении 30 атм. Каково давление, когда из баллона будет выпущена половина массы газа, а температура понизится до t2 = 10 0С?
13. Сосуд ёмкостью V = 0,01 м3 содержит азот массой m1 = 7 г и водород массой m2 = 1 г при температуре Т = 280 К. Определить давление P смеси газов.
14. Найти плотность ρ газовой смеси, состоящей по массе из одной части водорода и восьми частей кислорода, при давлении P = 0,1 МПа и температуре Т = 290 К.
15. Баллон емкостью V = 15 л содержит смесь водорода и азота при температуре Т = 300 К и давлении P = 1,23 МПа. Масса смеси m = 145 г. Определить массу m1 водорода и массу m2 азота.
16. Газовая смесь, состоящая из кислорода и азота, находится в баллоне под давлением P = 1 МПа. Считая, что масса кислорода составляет 20% от массы смеси, определить парциальные давления P1и P2от дельных газов.
17. Два сосуда с объемами V1 = 1 л и V2 = 3 л соединены трубкой с краном. До открытия крана в первом сосуде содержался азот под давлением P1 = 0,5 атм и при температуре t1 = 0 0С, а во втором - аргон под давлением P2 = 1,5 атм и при температуре t2 = 100 0С. Определить, какое давление установится в смеси газов, если открыть кран. Температура смеси 79 0С.
18. Плотность газа ρ при давлении P = 720 мм рт. ст. и температуре t2 = 0 0С равна 1,3 г/л. Найти массу моля μ газа.
19. Сколько молекул водорода находится в объеме 1,55 л при температуре 270С и давлении 750 мм рт. ст.?
20. Найти число молекул N в 1 см3 и плотность ρ азота при давлении 1,00×10-11 мм рт. ст. и температуре 15 0С.
21. Два баллона соединены трубкой с краном. В первом находится газ под давлением 105 Н/м2, во втором – при 6ּ104 Н/м2. Емкость первого баллона 1 л, второго – 3 л. Какое давление установится в баллонах (в мм рт. ст.), если открыть кран? Температуре постоянна. Объемом трубки можно пренебречь.
22. Найти число ν молей и число N молекул, содержащихся в объеме V = 1см3 водяного пара при температуре t = 4 0С.
23. В баллоне емкостью V = 20 л находится аргон под давлением P1 = 800 кПа и температуре Т1 = 325 К. когда из баллона было взято некоторое количество аргона, давление в баллоне снизилось до P2 = 600 кПа, а температура установилась Т2 = 300 К. Определить массу m аргона, взятого из баллона.
24. Баллон емкостью V = 40 л заполнен азотом. Температура азота Т = 300 К. Когда часть азота израсходовали, давление в баллоне понизилось на ∆P = 400 кПа. Определить массу израсходованного азота. Процесс считать изотермическим.
25. В баллоне находился идеальный газ при давлении 4ּ107 Па и температуре 300 К. Затем 3/5 содержащегося в баллоне газа выпустили, а температура понизилась до 240 К. Под каким давлением находится оставшийся в баллоне газ?
26. Какой объем V занимает смесь азота массой m1 = 1 кг и гелия m2 = 1 кг при нормальных условиях – давлении 760 мм рт. ст. и температуре 273 К?
27. Один баллон емкостью V1 = 20 л содержит азот под давлением P1 = 24 атм, другой – емкостью V2 = 44 л содержит кислород под давлением P2 = 16 атм. Оба баллона были соединены между собой и оба газа смешались, образовав однородную смесь (без изменения температуры). Найти парциальные давления P1 и P2 обоих газов в смеси и полное давление Р.
28. В сосуде при температуре t = 100 0С и давлении P = 4ּ105 Па находится 2 м3 смеси кислорода и сернистого газа SO2. Определить парциальные давления компонентов, если масса сернистого газа т2 = 9 кг.
29. Три баллона емкостью 3 л, 7 л и 5 л наполнены соответственно кислородом (2 атм), азотом (3 атм) и углекислым газом (0,6 атм) при одной и той же температуре. Баллоны соединяют между собой, причем образуется смесь той же температуры. Каково давление смеси?
30. Газовая смесь, состоящая из кислорода и азота, находится в баллоне под давлением P = 720 мм рт. ст. Считая, что масса кислорода составляет 40 % от массы смеси, определить концентрацию молекул отдельных газов при температуре 290 К.
31. Зная функцию распределения молекул по скорости, вывести формулу наиболее вероятной скорости.
32. Используя функцию распределения молекул по скорости, получить функцию, выражающую распределение молекул по относительным скоростям u (u = υ/υв).
33. Определить относительное число молекул идеального газа, скорости которых заключены в пределах от нуля до одной сотой наиболее вероятной скорости.
34. Какая часть молекул азота при 150 0С обладает скоростями от 300 до 325 м/с?
35. Какая часть молекул кислорода при 00С обладает скоростью от 100 до 110 м/с?
36. Какая часть молекул азота, находящегося при температуре Т, имеет скорости, лежащие в интервале от υв до υв +∆υ, где ∆υ = 20 м/с, Т = 400 К.
37. Определить температуру кислорода для которой функция распределения по скоростям будет иметь максимум при скорости υ = 420 м/с.
38. Определить температуру водорода, при которой средняя квадратичная скорость молекул больше их наиболее вероятной скорости на ∆υ = 400 м/с.
39. Во сколько раз средняя квадратичная скорость молекул водорода больше средней квадратичной скорости молекул водяных паров при той же температуре?
40. Азот находится под давлением p = 105 Па при температуре Т =300 К. Найти относительное число молекул азота, скорости которых лежат в интервале от υв до υв +∆υ, где ∆υ = 1 м/с.
41. Зная функцию распределения молекул по скоростям, определить среднюю арифметическую скорость <υ> молекул.
42. По функции распределения молекул по скоростям определить среднюю квадратичную скорость <υкв.>.
43. Найти среднюю арифметическую, среднюю квадратичную и наиболее вероятную скорости молекул газа, плотность которого при давлении 300 мм рт. ст. равна 0,3 г/л.
44. При какой температуре средняя квадратичная скорость молекул азота больше их наиболее вероятной скорости на 50 м/с?
45. Какая часть общего числа N молекул имеет скорости: 1) больше наиболее вероятной скорости и 2) меньше наиболее вероятной скорости?
46. Пылинки, взвешенные в воздухе, имеют массу m = 10-18 г. Во сколько раз уменьшится их концентрация n при увеличении высоты на ∆h =10 м? Температура воздуха Т = 300 К.
47. Масса т каждой из пылинок, взвешенных в воздухе, равна 1 аг. Отношение концентрации n1 пылинок на высоте h1 = 1 м к концентрации п0их на высоте h0= 0 равно 0,787. Температура воздуха Т = 300 К. Найти по этим данным значение постоянной Авогадро NA.
48. Насколько уменьшится атмосферное давление p = 100 кПа при подъеме наблюдателя над поверхностью Земли на высоту h = 100 м? Считать, что температура Т воздуха равна 290 К и не изменяется с высотой.
49. На какой высоте h над поверхностью Земли атмосферное давление вдвое меньше, чем на её поверхности? Считать, что температура Т воздуха равна 290 К и не изменяется с высотой.
50. Барометр в кабине летящего вертолета показывает давление p = 90 кПа. На какой высоте h летит вертолет, если на взлетной площадке барометр показывал давление p0 = 100 кПа? Считать, что температура Т воздуха равна 290 К и не изменяется с высотой.
51. Найти изменение высоты ∆h, соответствующее изменению давления на ∆p = 100 Па, в двух случаях: 1) вблизи поверхности Земли, где температура T1= 290 К, давление p1 = 100 кПа; 2) на некоторой высоте, где температура Т2 = 220 К, давление p2 = 25 кПа.
52. Барометр в кабине летящего самолета все время показывает одинаковое давление p = 80 кПа, благодаря чему летчик считает высоту h полета неизменной. Однако температура воздуха изменилась на ∆Т = 1 К. Какую ошибку ∆h в определении высоты допустил летчик? Считать, что температура не зависит от высоты и что у поверхности Земли давление p0 = 100 кПа.
53. Высотная космическая станция расположена на горе Алагез в Армении на высоте 3250 м над уровнем моря. Найти давление воздуха на этой высоте. Температуру воздуха считать постоянной и равной 50С. Массу одного киломоля воздуха принять равной 29 кг/моль. Давление воздуха на уровне моря равно 760 мм рт. ст.
54. На какой высоте давление воздуха составляет 75 % от давления на уровне моря? Температуру считать постоянной и равной 0 0С.
55. Пассажирский самолет совершает полеты на высоте 8300 м. чтобы не снабжать пассажиров кислородными масками, в кабинах при помощи компрессора поддерживается постоянное давление, соответствующее высоте 2700 м. Найти разность давлений внутри и снаружи кабины. Среднюю температуру наружного воздуха считать равной 0 0С.
56. Найти в предыдущей задаче, во сколько раз плотность воздуха в кабине больше плотности воздуха вне её, если температура наружного пространства равна минус 200С и температура внутри кабины 200С.
57. Какова масса 1 м3 воздуха: 1) у поверхности Земли, 2) на высоте 4км от поверхности Земли? Температуру воздуха считать постоянной и равной 00С. Давление воздуха у поверхности Земли равно 105 Па.
58. На какой высоте плотность газа составляет 50 % от его плотности на уровне моря? Температуру считать постоянной и равной 0 0С. Задачу решить для: 1) воздуха и 2) водорода.
59. На поверхности Земли барометр показывает 101 кПа. Каково будет давление при подъеме барометра на высоту 540 м. Температуру считать одинаковой и равной 7 0С.
60. Определить высоту горы, если давление на её вершине равно половине давления на уровне моря. Температура всюду одинакова и равна 0 0С.
61. Найти количество азота, прошедшего вследствие диффузии через площадку 10 см2 за 5 с, если градиент плотности азота в направлении, перпендикулярном площадке, 1,26 мг/см4. Коэффициент диффузии 1,42 см2/с.
62. За какое время 720 мг углекислого газа продиффундируют из почвы в атмосферу через 1 м2 её поверхности при градиенте плотности 500 мг/см4? Коэффициент диффузии принять равным 1,42 см2/с.
63. Определить динамическую вязкость кислорода при нормальных условиях. Принять среднюю длину свободного пробега молекул 100 нм.
64. При некоторых условиях длина свободного пробега молекул водорода равна 0,5 мкм. Определить диаметр молекулы, если эти условия таковы: давление 0,2 МПа, температура 17 0С.
65. Найти количество азота, прошедшего вследствие диффузии через площадку 100 см2 за 10 с, если градиент плотности в направлении, перпендикулярном к площадке, равен 1,26 кг/м4.
66. Коэффициенты диффузии и внутреннего трения кислорода при некоторых условиях соответствуют 0,12 Мм2/с и 19,5 мкПаּс. Найти при этих условиях плотность кислорода.
67. В сосуде объемом 2 л находится 4,0ּ1022 молекул двухатомного газа. Коэффициент диффузии равен 2,0ּ10-5 м2/с. Определить коэффициент теплопроводности газа при этих условиях.
68. Какой толщины следовало бы сделать деревянную стену здания, чтобы она давала такую же потерю теплоты, как кирпичная стена толщиной 40 см при одинаковых температурах внутри и снаружи здания? Коэффициенты теплопроводности кирпича и дерева равны соответственно 0,70 и 0,175 Вт/(мּК).
69. Между двумя пластинками, находящимися на расстоянии 1 мм друг от друга, находится воздух. Между пластинками поддерживается разность температур 10С. Площадь каждой пластины равна 100 см2. Какое количество тепла передается за счет теплопроводности от одной пластины к другой за 10 мин? Считать, что воздух находится при нормальных условиях. Диаметр молекулы равен 0,3 нм.
70. Найти коэффициент теплопроводности водорода, если известно, что коэффициент внутреннего трения для него при этих условиях 8,6 мкПаּс.
71. Средняя длина свободного пробега молекулы углекислого газа при нормальных условиях равна 50 нм. Определить среднюю арифметическую скорость молекулы и число соударений, которое испытывает молекула. d = 0,7 нм.
72. В колбе объемом 100 см3 находится 0,5 г азота. Найти среднюю длину свободного пробега молекул азота при этих условиях, d = 0,3 нм.
73. В сосуде объемом 0,5 л находится кислород при нормальных условиях. Найти общее число столкновений между молекулами кислорода за одну минуту. d = 0,3 нм.
74. Найти среднее время между двумя последовательными столкновениями молекул азота при температуре 10 0С и давлении 1 мм рт. ст. d = 0,3 нм.
75. Какое предельное число молекул газа должно находиться в 1 см3 сферического сосуда диаметром 15 см, чтобы молекулы не сталкивались друг с другом? Диаметр молекулы газа принять равным 0,3 нм.
76. Как изменится число ударов молекул одноатомного газа о стенку баллона площадью 1м2 за 1 с, если давление газа увеличится в 4 раза в 1) изотермическом и 2) изохорном процессах?
77. При каком давлении средняя длина свободного пробега молекул азота равна 1 мм, если при нормальном давлении она равна 8ּ10-6 см?d = 0,3 нм.
78. Плотность фотосферы, оцениваемая оптическими методами, составляет 2ּ10-4кг/м3. Определить длину свободного пробега атомов водорода в фотосфере, d = 0,23 нм.
79. В сосуде вместимостью 1 дм3 находится азот при температуре 7 0С и давлении 0,2 МПа. Определить число столкновений молекул азота в этом сосуде за 1с, d = 0,3 нм.
80. Какое давление нужно создать в колбе диаметром 0,1 м, содержащей азот при температуре 20 0С, чтобы получить вакуум? d = 0,3 нм.
81. Средняя длина свободного пробега молекул водорода при некотором давлении и температуре 21 0С равна 90 нм. В результате изотермического процесса давление газа увеличилось в 3 раза. Найти среднее число столкновений молекул водорода за 1 с в конце процесса. d = 0,23 нм.
82. При каком давлении средняя длина свободного пробега молекул водорода равна <λ> = 2,5 см? Температура t =68 0С, d = 0,23 нм.
83. В баллоне вместимостью 10 дм3 находится гелий массой 2 г. Определить среднюю длину свободного пробега молекул гелия, d = 0,2 нм.
84. Средняя длина свободного пробега молекул гелия при нормальных условиях 230 нм. Найти среднюю продолжительность свободного пробега молекул гелия при давлении 1,0 МПа и температуре 17 0С, d = 0,2 нм.
85. В сферическом сосуде вместимостью 2 дм3 находится водород. При какой плотности водорода молекулы его практически не будут сталкиваться друг с другом? d = 0,23 нм.
86. Определить коэффициент диффузии двухатомного газа, находящегося в сосуде объемом 2,0 л с числом молекул 4,0ּ1022, если коэффициент теплопроводности этого газа 144 мВт/(мּК).
87. Определить среднюю длину свободного пробега молекул кислорода, если при температуре 0 0С коэффициент диффузии кислорода 0,20 см2/с, d = 0,3 нм.
88. Найти коэффициент теплопроводности водорода, если коэффициент вязкости для него при этих условиях 8,6 мкПаּс.
89. Определить коэффициент диффузии гелия, если средняя длина свободного пробега атомов гелия при нормальных условиях 180 нм.
90. Углекислый газ и азот находятся при одинаковых температурах и давлениях. Найти для этих газов отношение коэффициентов диффузии, внутреннего трения, теплопроводности. Диаметры молекул этих газов: d1 = 0,4 нм, d2 = 0,3 нм.
Основные положения термодинамики
Термодинамика – раздел физики, изучающий общие свойства макроскопических систем и процессы перехода между различными состояниями. В основе термодинамики лежат установленные из опыта и подтверждающиеся всей совокупностью вытекающих из них следствий законы, называемые началами термодинамики.
Первое начало термодинамики по существу представляет собой закон сохранения энергии, примененный к термодинамическим процессам: количество теплоты, сообщенное термодинамической системе, идет на увеличение ее внутренней энергии DU и совершение системой работы против внешних сил.
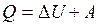 .
.
Для процессов, в которых термодинамические параметры системы меняются бесконечно мало можно записать первое начало в дифференциальной форме.
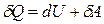 .
.
Под внутренней энергией системы подразумевают энергию этой системы за вычетом кинетической энергии системы как целого и потенциальной энергии системы в поле внешних сил. Внутренняя энергия, в отличие от работы и количества теплоты, является функцией состояния. Выражение для внутренней энергии предельно упрощается при рассмотрения простейшей термодинамической системы – идеального газа. В этом случае
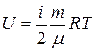 .
.
где i - число степеней свободы молекул газа (i = 3 для одноатомного, i = 5 для двухатомного, i = 6 для многоатомного газа с жесткой связью между атомами в молекуле).
Элементарная работа, совершаемая газом против внешних сил при изменении его объема: 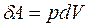 . При изменении объема газа от V1 до V2 газ совершит работу
. При изменении объема газа от V1 до V2 газ совершит работу
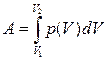 .
.
где p(V) - зависимость давления от объема в процессе расширения газа. Для изобарического процесса эта формула принимает вид
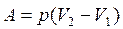 ,
,
а для изотермического
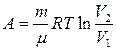 .
.
Для расчета количества теплоты, переданного системе, вводится понятие теплоемкости – величины, равной количеству теплоты, необходимому для нагревания вещества на 1 К: 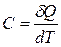 . Удобно ввести также удельную теплоемкость – величину, равную количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К:
. Удобно ввести также удельную теплоемкость – величину, равную количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К: 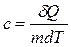 и молярную теплоемкость – величину, равную количеству теплоты, необходимому для нагревания одного моля вещества на 1 К:
и молярную теплоемкость – величину, равную количеству теплоты, необходимому для нагревания одного моля вещества на 1 К: 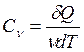 . Удельная теплоемкость связана с молярной соотношением
. Удельная теплоемкость связана с молярной соотношением 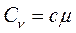 .
.
Различают теплоемкости при постоянном давлении и постоянном объеме, если в процессе нагревания вещества поддерживается постоянным соответственно давление или объем. В случае нагревания при постоянном объеме не совершается работа против внешних сил, поэтому теплоемкость при постоянном объеме меньше теплоемкости при постоянном давлении. Применяя первое начало термодинамики, можно получить выражения для молярных теплоемкостей при постоянном объеме и давлении, а также уравнение связи между ними:
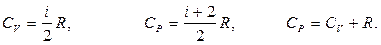
Последнее выражение называется уравнением Майера.
Адиабатическим называется процесс, происходящий без теплообмена с окружающей средой, при адиабатическом процессе давление, объем и температура газа связаны уравнениями Пуассона:

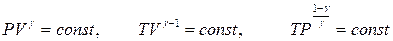 ,
,
где 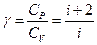 - отношение теплоемкостей при постоянном давлении и объеме, которое называют показателем адиабаты или коэффициентом Пуассона. Работа в адиабатическом процессе совершается за счет убыли внутренней энергии
- отношение теплоемкостей при постоянном давлении и объеме, которое называют показателем адиабаты или коэффициентом Пуассона. Работа в адиабатическом процессе совершается за счет убыли внутренней энергии 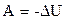 и выражается следующими формулами:
и выражается следующими формулами:
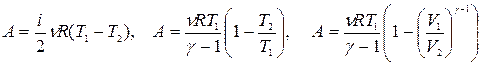 .
.
Круговым процессом или циклом называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное. Коэффициентом полезного действия тепловой машины называется выражение, определяемое формулами:
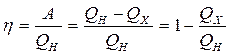 ,
,
где А - работа, совершенная рабочим веществом тепловой машины за цикл, QН - количество теплоты, полученное рабочим веществом от нагревателя, QХ - количество теплоты, отданное рабочим веществом холодильнику за то же время.
Второе начало термодинамики определяет направление протекания термодинамических процессов и может быть сформулировано несколькими эквивалентными способами. Наиболее часто встречаются формулировки Клаузиуса и Томсона: 1) невозможен процесс, единственным результатом которого является передача теплоты от холодного тела к горячему; 2) невозможен процесс, единственным результатом которого является совершение работы за счет охлаждения одного тела. Основываясь на втором начале термодинамики, Карно вывел теорему, носящую его имя: из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателя и холодильника, наибольшим КПД обладают обратимые машины; при этом КПД обратимых машин, работающих при одинаковых температурах нагревателей и холодильников, равны друг другу и не зависят от конструкции машин. Введя в рассмотрение абстрактный обратимый цикл, состоящий из двух изотерм и двух адиабат, Карно установил формулу максимально возможного КПД тепловой машины 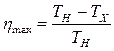 (ТН, ТХ - температуры нагревателя и холодильника).
(ТН, ТХ - температуры нагревателя и холодильника).
Введя специальную функцию состояния системы - энтропию S, можно дать еще одну формулировку второго начала термодинамики: энтропия адиабатически изолированной системы при любых процессах, происходящих в ней, не уменьшается - она возрастает при необратимых процессах и остается постоянной при обратимых 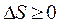 . Если система совершает переход из состояния 1 в состояние 2, то изменение энтропии
. Если система совершает переход из состояния 1 в состояние 2, то изменение энтропии
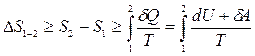 ,
,
(знак равенства относится к обратимым процессам). Физический смысл энтропии раскрывает формула Больцмана 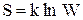 , где k - постоянная Больцмана,W - термодинамическая вероятность состояния системы - число способов, которыми может быть реализовано данное состояние макросистемы.
, где k - постоянная Больцмана,W - термодинамическая вероятность состояния системы - число способов, которыми может быть реализовано данное состояние макросистемы.
Примеры решения задач
Задача № 1
Газ, занимавший объем 2 л при давлении 0,1 МПа, расширился изотермически до 4 л. После этого, охлаждая газ изохорически, уменьшили давление в 2 раза. Далее газ изобарически расширился до 8 л. Начертите график зависимости давления от объема, найдите работу, совершенную газом.
Дано: V1 = 2 л P1= 0,1 МПа V2 = 4 л P3 = 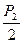 V3 = 8 л V3 = 8 л |
| A - ? |
Решение:
Построим график зависимости давления от объема. Первый процесс, происходящий с газом, является изотермическим. Выразим давление через объём и температуру при помощи уравнения Менделеева – Клапейрона 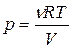 . Так как T = const, давление в данном процессе обратно пропорционально объёму, и линия, изображающая данный процесс на p-V диаграмме, будет участком гиперболы начинающейся в точке V1, p1 и заканчивающейся в точке V2, p2.
. Так как T = const, давление в данном процессе обратно пропорционально объёму, и линия, изображающая данный процесс на p-V диаграмме, будет участком гиперболы начинающейся в точке V1, p1 и заканчивающейся в точке V2, p2.
Второй процесс, происходящий с газом, является изохорическим. В этом процессе объём не изменяется и, следовательно, на P-V диаграмме он изображается в виде вертикальной прямой, идущей из точки V2, p2 в точку V2, p3.
Третий процесс происходящий с газом, по условию задачи, изобарический. На P-V диаграмме он будет выглядеть как горизонтальная линия, идущая из точки V2, p3 в точку V3, p3.
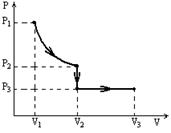 Последовательно изображая все процессы, получим следующую P-V диаграмму.
Последовательно изображая все процессы, получим следующую P-V диаграмму.
Рассчитаем работу, совершенную газом. Так как работа, совершаемая газом, - аддитивная величина
А = А1+А2+А3 ,
где А1 – работа, совершенная в изотермическом процессе, А2 – работа, совершенная в изохорическом процессе, А3 – работа, совершенная в изобарическом процессе. Каждую из работ можно вычислить по формуле 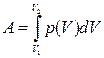 (V1 и V2 – начальные и конечные объёмы занимаемые газом). Применим эту формулу для определения работы А1. Согласно уравнению Менделеева – Клапейрона, зависимость p(V) имеет вид
(V1 и V2 – начальные и конечные объёмы занимаемые газом). Применим эту формулу для определения работы А1. Согласно уравнению Менделеева – Клапейрона, зависимость p(V) имеет вид 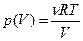 .
.
Следовательно, работа 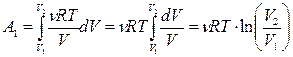 . Множитель
. Множитель 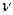 RT вынесем из-под знака интеграла как постоянную величину, заменяя её на p1V1, получим
RT вынесем из-под знака интеграла как постоянную величину, заменяя её на p1V1, получим
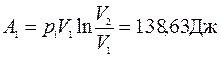 .
.
В изохорическом процессе изменение объёма газа не происходит, следовательно, А2 = 0.
При вычислении работы А3 учтём, что давление, как постоянная величина, может быть вынесена из под знака интеграла
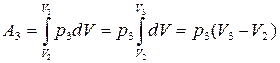 .
.
Для расчёта необходимо знать давление P3. Так как первый процесс изотермический, 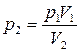 . По условию задачи
. По условию задачи 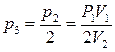 , следовательно,
, следовательно,
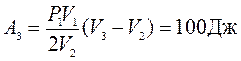 .
.
Общая работа А = А1+А2+А3 = 238,63 Дж.
Ответ: работа, совершенная газом А = 238,63 Дж.
В качестве дополнения заметим, что существует еще один способ определения работы, совершаемой газом, – графический. Как известно, площадь на диаграмме p-V между линией, изображающей процессы, происходящие с газом, и осью объема по модулю равна работе. Если объём газа увеличится, то работа положительна, в противном случае - отрицательна. В ряде случаев этот метод позволяет найти работу, не прибегая к вычислению интегралов.
Задача № 2
Азот находящийся при температуре 400 К, подвергли адиабатическому расширению, в результате которого его объём увеличился в n = 5 раз, а внутренняя энергия уменьшилась на 4 кДж. Определите массу азота, считая его идеальным газом.
Дано: 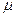 =28 г/моль i = 5 T1 = 400 K V2 = nV1 n = 5 ΔU = - 4 кДж =28 г/моль i = 5 T1 = 400 K V2 = nV1 n = 5 ΔU = - 4 кДж |
| m -? |
Решение:
Составим выражение изменения внутренней энергии азота, считая его идеальным газом.
ΔU = 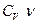 ΔT =
ΔT = 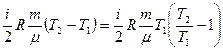
Учитывая, что процесс расширения происходил адиабатически, воспользуемся уравнением Пуассона, связывающим температуры и объёмы 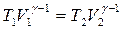 (
( 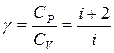 -показатель адиабаты). С помощью данного уравнения сведём неизвестное отношение температур к известному отношению объёмов:
-показатель адиабаты). С помощью данного уравнения сведём неизвестное отношение температур к известному отношению объёмов: 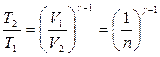 .
.
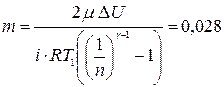 Для изменения внутренней энергии в итоге получаем формулу
Для изменения внутренней энергии в итоге получаем формулу 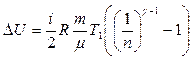 .
.
Выразив массу и произведя расчеты, получим кг.
Ответ: масса азота m = 0.028 кг.
Задача № 3
