Когерентность источников света

Содержание

1. Цель работы…………………………………….………….…….…….4

2. Теоретическая часть…………………….………………….………….4

2.1.Интерференция света……………………………………….…….4

2.2. Когерентность источников света…..……….…………….……..6

2.3. Интерференция в тонких плёнках…….…..……………….……9

3. Экспериментальная часть…………….….…..……………….……....9

3.1. Приборы и принадлежности……….…..….……………………13

3.2. Описание установки………………….….….……………….….13

3.3. Требования по технике безопасности….………………………15

3.4. Порядок выполнения работы…………….………………….…16

4. Контрольные вопросы……………………….………………….……18

Список литературы……………………..……………………….……...18

Лабораторная работа № 72

Изучение интерференции света в клиньях

Цель работы

Наблюдение полос равной толщины и определение малого угла воздушного клина в зазоре между стеклянными пластинками по интерференционной картине полос равной толщины.

Теоретическая часть

Интерференция света

Интерференция - одно из проявления волновых свойств света. Интерференция - частный случай сложения волн, при котором наблюдается устойчивая во времени картина перераспределения в пространстве энергии световых волн. Зрительно это проявляется в том, что возникают геометрические места (точки, линии, области) с минимальной и максимальной освещённостью, т.е. тёмные и светлые. На рис. 1 приведены интерференционные картины, полученные разными способами, и указаны области минимальной и максимальной освещенностей.

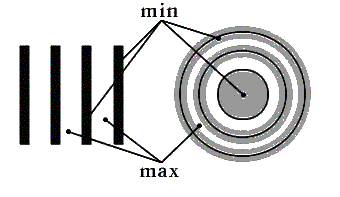
Рис. 1

До появления лазеров интерференция могла наблюдаться только при разведении и последующем сведении лучей, исходящих из одного и того же источника в разных приборах и установках. Из естественных проявлений интерференции света наиболее известно радужное окрашивание тонких плёнок (масляные плёнки на воде, мыльные пузыри, окисные плёнки на металлах), возникающие вследствие сложения волн, отражённых двумя поверхностями плёнки.

Пусть две волны одинаковой частоты, накладываясь друг на друга, возбуждают в некоторой точке пространства колебания одинакового направления

E₁ = a₁ cos(ωt+φ₁), (1)

E₂ = a₂ cos(ωt+φ₂). (2)

Для нахождения результирующей амплитуды воспользуемся графическим методом.

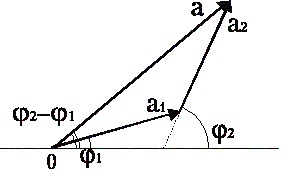
Рис. 2

Используя теорему косинусов можно записать:

а² =а₁² + а₂² + 2а₁а₂ cos(φ₂ – φ₁) (3)

и т.к. I ~ а², то

I = I₁ + I₂ + 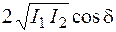. (4)

Если разность фаз δ = (φ₂ – φ₁) постоянна во времени (δ = const), то такие волны называются когерентными. Если волны некогерентны, то δ непрерывно хаотически меняется, принимая с равной вероятностью любые значения.

Особенно отчётливо интерференция проявляется, когда интенсивности интерферирующих волн одинаковы:

I₁ = I₂ = I. (5)

1.В случае некогерентных волн δ меняется случайным образом с частотой порядка частоты света видимого диапазона (ν ~ 10¹⁵гц). Т.к. всякий фотоприёмник (в частности, человеческий глаз) обладает инерционностью, то он усреднит значение cos δ, но среднее значение <cos δ> = 0. Поэтому для некогерентных волн

I = I₁ + I₂, (6)

т.е. при сложении некогерентных волн происходит простое сложение интенсивностей световых волн во всех точках пространства.

2.В случае когерентных волн δ = const и в зависимости от значения δ будет наблюдаться либо увеличение, либо уменьшение интенсивности.

Рассмотрим случай когда а₁ = а₂, т.е. I₀ = I₁ =I₂.

В этом случае из (4) имеем

I = 2I₀ + 2I₀cos δ, (7)

cos δ может принимать значения от +1 до –1 в зависимости от значения δ:

а) пусть cos δ = – 1,

тогда I = 2I₀ – 2I₀ = 0, т.е. наблюдается ослабление (минимум).

Но cos δ = –1 при δ = π, 3π, 5π,…(2 k +1) π, где k = 0, 1, 2…

Обычно когерентные волны получают, разделяя одну волну на две. Поэтому начальные фазы колебаний в (1) и (2)
равны, а разность фаз δ возникает за счёт различных путей, проходимых лучами. Следовательно

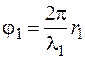_, (8)

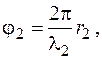(9)

где r₁ и r₂ - геометрические пути лучей. Проходимых ими от источника до точки, где они складываются, λ₁ и λ₂ - длины волн этих лучей. Следует учесть, что 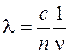, с - скорость света в вакууме, n - показатель преломления среды, в которой распространяется луч, ν - частота света. При переходе света из одной среды в другую изменяется λ (т.к. изменяется скорость света), но ν остаётся при этом неизменным.

Если оба луча распространяются в одной среде, то n₁ = n₂ = n и (8) и (9) будут

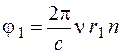, (10)

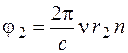. (11)

Учитывая, что δ = (φ₂ – φ₁) окончательно получаем

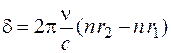. (12)

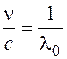, где λ₀ - длина световой волны в вакууме. Откуда

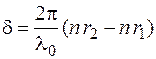. (13)

Величина n r называется оптическим путём, а (n r₂ – n r₁) = Δ - оптической разностью хода лучей. Учитывая условие минимума

Δ = (2k + 1) π, (14)

получаем

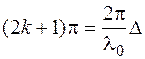, (15)

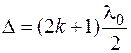, k = 0, 1, 2…

Итак, условием минимума при интерференции когерентных лучей является

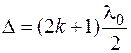. (16)

Для минимума оптическая разность хода интерферирующих лучей равна нечётному числу полуволн.

б) пусть cos δ = +1,

тогда из (7) имеем I = 2I₀ + 2I₀ =4I₀, т.е. наблюдается усиление (максимум), но cos δ = +1 при δ = 0, 2π, 4π, 6π,…2kπ, где k = 0, 1, 2,… проводя рассуждения аналогичные п. а) можно получить условие максимума

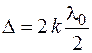. (17)

Для максимума оптическая разность хода интерферирующих лучей равна чётному числу полуволн.

Таким образом, при сложении когерентных волн происходит сложение амплитуд волн с учётом разности их фаз, что приводит к увеличению интенсивности света в одних точках пространства и уменьшению в других.

Когерентность источников света

Опыт показывает, что, взяв естественные источники света, интерференцию получить нельзя. Это связано с тем, что все естественные источники света являются некогерентными. Объясняется это тем, что излучение естественных источников слагается из излучений многих атомов. Отдельный атом испускает отдельные цуги волн длительностью τ ~ 10^-8–10^-9 с длиной (~10÷100 мкм). Фаза колебаний одного цуга никак не связана с фазой колебаний другого, т.е. меняется случайным образом. Т.о. волна от одного источника, состоящего из множества цугов, с течением времени меняется. Аналогично фаза колебаний от другого источника также меняется случайным образом с течением времени. Результатом является то, что разность фаз между волнами от естественных источников с течением времени изменяется δ(t) = Ф₂(t) – Ф₁(t), при этом I = I₁+I₂.

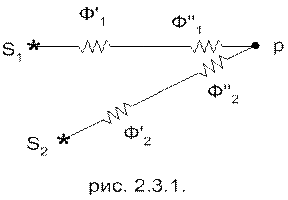
Рис. 3

Когерентные световые волны можно получить, разделяя одну световую волну на 2 части, каждая из которых проходит свой оптический путь L₁ и L₂.

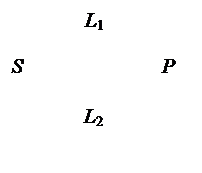
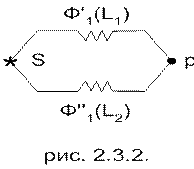
Рис. 4

В этом случае в каждый момент времени будут складываться волны одного цуга, и разность фаз будет определяться только оптической разностью хода Δ

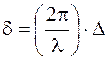. (18)

При этом следует иметь в виду, что Δ не может быть очень большой (Δ = L₂ – L₁), Δ ~ 10 ÷ 100 мкм. В противном случае в точку волна 1-ая придет намного раньше, чем 2-я, т.е. они не встретятся и интерференционная картинка не получится.

Максимальное значение Δ, при котором еще происходит интерференция, называется длиной когерентности.

Когерентными являются волны, у которых:

1. ω₁ = ω₂ или ν₁ = ν₂ ,

2. φ₁ – φ₂ = const,

3. E₁║E₂.

Условие 3 означает, что колебания должны быть одинаково направлены, т.е. интерферирующие лучи должны быть поляризованы в одной плоскости.