Свойства эрмитового сопряжения
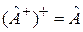 ,
,
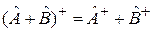 ,
,
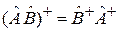 ,
,
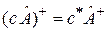 ,
, 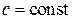 . (2.12)
. (2.12)
Для доказательства 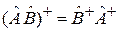 применяем (2.11) к оператору
применяем (2.11) к оператору 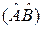
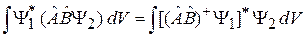
и последовательно – вначале к оператору 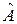 , затем, к
, затем, к 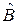
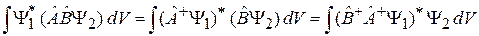 .
.
Сравниваем правые стороны полученных равенств.
Остальные соотношения доказать самостоятельно.
Эрмитовый оператор не изменяется при эрмитовом сопряжении
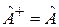 . (2.13)
. (2.13)
Из (2.11) получаем определение эрмитового оператора
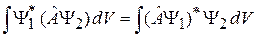 . (2.14)
. (2.14)
Следовательно, эрмитовый оператор можно переставлять в интегральной квадратичной форме от одной функции к другой.
Свойства эрмитова оператора:
1) Собственные значения вещественные.
Доказательство:
В (2.14)
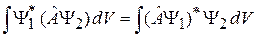
полагаем 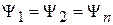 , где
, где 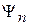 – собственная функция оператора
– собственная функция оператора 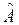 . Учитываем
. Учитываем
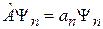 ,
, 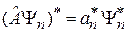 ,
,
получаем
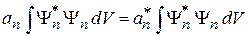 .
.
Следовательно,
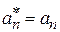 (2.15)
(2.15)
– измеряемая величина вещественна.
2) Собственные функции, соответствующие разным собственным значениям, взаимно ортогональны.
Доказательство:
Для собственных функций 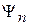 и
и 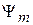 оператора
оператора 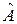 выполняется
выполняется
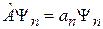 ,
, 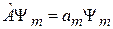 ,
, 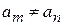 ,
, 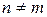 .
.
Из (2.14)
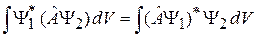
при 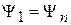 ,
, 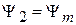 получаем
получаем
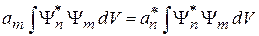 .
.
Учитывая вещественность собственных значений (2.15), находим
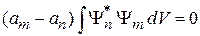 .
.
При 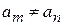 выполняется условие ортогональности состояний
выполняется условие ортогональности состояний
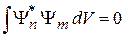 . (2.16)
. (2.16)
Следовательно, состояния 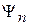 и
и 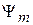 при измерении не совместимы и измерение дает однозначный результат.
при измерении не совместимы и измерение дает однозначный результат.
