Амплитуда и фаза вынужденных колебаний

Механических и электромагнитных).

Резонанс

Рассмотрим зависимость амплитуды Авынужденных колебаний от частоты w. Механические и электромагнитные колебания будем рассматривать одновременно, называя колеблющуюся величину либо смещением (х)колеблющегося тела из положения равновесия, либо зарядом (Q) конденсатора.

Из формулы (147.8) следует, что амплитуда А смещения (заряда) имеет максимум. Чтобы определить резонансную частоту w_рез — частоту, при которой амплитуда А смещения (заряда) достигает максимума, — нужно найти максимум функции (147.8), или, что то же самое, минимум подкоренного выражения. Продифференцировав подкоренное выражение по w и приравняв его нулю, получим условие, определяющее w_рез

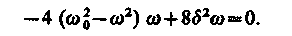
Это равенство выполняется при w = 0, 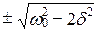, у которых только лишь положи тельное значение имеет физический смысл. Следовательно, резонансная частота

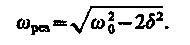(148.1)

Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы (частоты вынуждающего переменного напряжения) к частоте, равной или близкой собственной частоте колебательной системы, называется резонансом (соответственно механическим или электрическим). При d² ≪ w²₀ значение w_рез, практически совпадает с собственной частотой w₀ колебательной системы. Подставляя (148.1) в формулу (147.8), получим

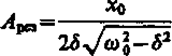(148.2)

На рис. 210 приведены зависимости амплитуды вынужденных колебаний от частоты при различных значениях d. Из (148.1) и (148.2) вытекает, что чем меньше d, тем выше и правее лежит максимум данной кривой. Если w®0, то все кривые (см. также (147.8)) достигают одного и того же, отличного от нуля, предельного значения x₀/w²₀, которое называют статическим отклонением. В случае механических колебаний x₀/w²₀ = F₀/(mw²₀) в случае электромагнитных — U_m/(Lw²₀).Если w®¥, то все кривые асимптотически стремятся к нулю. Приведенная совокупность кривых называется резонансными кривыми.

Рис. 210

Из формулы (148.2) вытекает, что при малом затухании (d² ≪ w²₀) резонансная амплитуда смещения (заряда)

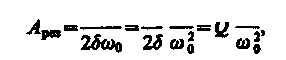
где Q — добротность колебательной системы (см. (146.8)), x₀/w²₀ — рассмотренное выше статическое отклонение. Отсюда следует, что добротность Qхарактеризует резонансные свойства колебательной системы: чем больше Q, тем больше А_рез.

На рис. 211 представлены резонансные кривые для амплитуды скорости (тока).

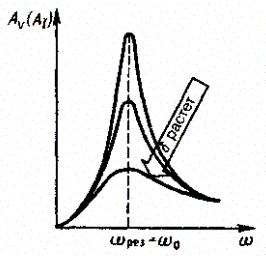
Рис. 211

Амплитуда скорости (тока)

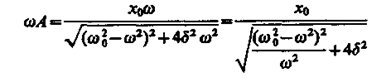
максимальна при w²₀ = w₀ и равна x₀/(2d), т. е. чем больше коэффициент затухания d, ниже максимум резонансной кривой. Используя формулы (142.2), (146.10) и (143.4), (146.11), получим, что амплитуда скорости при механическом резонансе равна

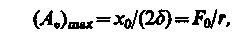
а амплитуда тока при электрическом резонансе

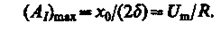
Из выражения tgj = 2dw/( w²₀ - w²) (см. (147.9)) следует, что если затухание в системе отсутствует (d = 0), то только в этом случае колебания и вынуждающая сила (приложенное переменное напряжение) имеют одинаковые фазы; во всех других случаях j ¹ 0.

Зависимость jот wпри разных коэффициентах dграфически представлена на рис. 212, из которого следует, что при изменении w изменяется и сдвиг фаз j. Из формулы (147.9) вытекает, что при w = 0 j = 0, а при w = w₀ независимо от значения коэффициента затухания j= p/2, т. е. сила (напряжение) опережает по фазе колебания на p/2. При дальнейшем увеличении w сдвиг фаз возрастает и при w ≫ w j ® p, т.е. фаза колебаний почти противоположна фазе внешней силы (переменного напряжения). Семейство кривых, изображенных на рис. 212, называется фазовыми резонансными кривыми.

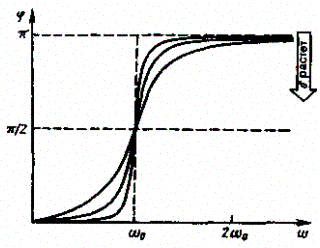
Рис. 212

Явления резонанса могут быть как вредными, так и полезными. Например, при конструировании машин и различного рода сооружений необходимо, чтобы собственная частота колебаний их не совпадала с частотой возможных внешних воздействий, в противном случае возникнут вибрации, которые могут вызвать серьезные разрушения. С другой стороны, наличие резонанса позволяет обнаружить даже очень слабые колебания, если их частота совпадает с частотой собственных колебаний прибора. Так, радиотехника, прикладная акустика, электротехника используют явление резонанса.

Переменный ток

Установившиеся вынужденные электромагнитные колебания (см. § 147) можно рас сматривать как протекание в цепи, содержащей резистор, катушку индуктивности и конденсатор, переменного тока. Переменный ток можно считать квазистационарным, т. е. для него мгновенные значения силы тока во всех сечениях цепи практически одинаковы, так как их изменения происходят достаточно медленно, а электромагнитные возмущения распространяются по цепи со скоростью, равной скорости света. Для мгновенных значений квазистационарных токов выполняются закон Ома и вытекающие из него правила Кирхгофа, которые будут использованы применительно к переменным токам (эти законы уже использовались при рассмотрении электромагнитных колебаний).

Рассмотрим последовательно процессы, происходящие на участке цепи, содержащем резистор, катушку индуктивности и конденсатор, к концам которого приложено переменное напряжение

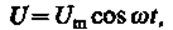(149.1)

где U_m — амплитуда напряжения.

1. Переменный ток, текущий через резистор сопротивлением R (L®0, C®0) (рис. 213, а). При выполнении условия квазистационарности ток через резистор определяется законом Ома:

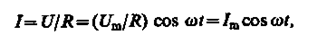
где амплитуда силы тока I_m = U_m/R.

Рис. 213

Для наглядного изображения соотношений между переменными токами и напряжениями воспользуемся методом векторных диаграмм. На рис. 213, б дана векторная диаграмма амплитудных значений тока I_m и напряжения U_m на резисторе (сдвиг фаз между I_m и U_m равен нулю).

2. Переменный ток, текущий через катушку индуктивностью L(R®0, С®0) (рис. 214, а).

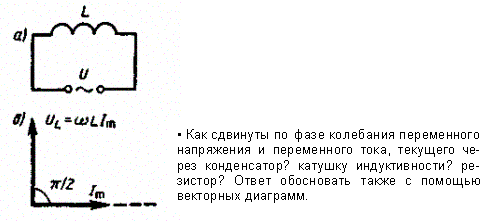
Рис. 214

Если в цепи приложено переменное напряжение (149.1), то в ней потечет переменный ток, в результате чего возникнет э.д.с. самоиндукции (см. (126.3)) ℰ_s = 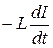. Тогда закон Ома (см. (100.3)) для рассматриваемого участка цепи имеет вид

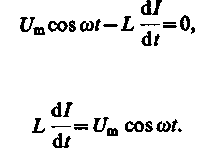(149.2)

Так как внешнее напряжение приложено к катушке индуктивности, то

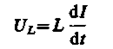(149.3)

есть падение напряжения на катушке. Из уравнения (149.2) следует, что

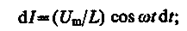
после интегрирования, учитывая, что постоянная интегрирования равна нулю (так как отсутствует постоянная составляющая тока), получим

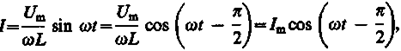(149.4)

где I_m= U_m/(wL). Величина

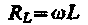(149.5)

называется реактивным индуктивным сопротивлением (или индуктивным сопротивлением). Из выражения (149.5) вытекает, что для постоянного тока (w = 0) катушка индуктивности не имеет сопротивления. Подстановка значения U_m = wLI_m в выражение (149.2) с учетом (149.3) приводит к следующему значению падения напряжения на катушке индуктивности:

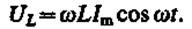(149.6)

Сравнение выражений (149.4) и (149.6) приводит к выводу, что падение напряжения U_Cопережает по фазе ток I, текущий через катушку, на p/2, что и показано на векторной диаграмме (рис. 214, б).

3.Переметни ток, текущий через конденсатор емкостью С(R®0, L®0) (рис. 215, а).

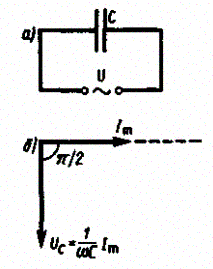
Рис. 215

Если переменное напряжение (149.1) приложено к конденсатору, то он все время перезаряжается, и в цепи течет переменный ток. Так как все внешнее напряжение приложено к конденсатору, а сопротивлением подводящих проводов можно пренебречь, то

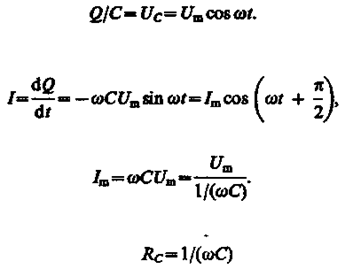
называется реактивным емкостным сопротивлением (или емкостным сопротивлением). Для постоянного тока (w = 0) R_C®¥, т. е. постоянный ток через конденсатор течь не может. Падение напряжения на конденсаторе

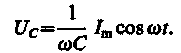(149.8)

Сравнение выражений (149.7) и (149.8) приводит к выводу, что падение напряжения U_C отстает по фазе от текущего через конденсатор тока I на p/2. Это показано на векторной диаграмме (рис. 215, б).

4. Цепь переменного тока, содержащая последовательно включенные резистор, катушку индуктивности и конденсатор. На рис. 216, а представлен участок цепи, содержащий резистор сопротивлением R, катушку индуктивностью Lи конденсатор ем костью С, к концам которого приложено переменное напряжение (149.1).

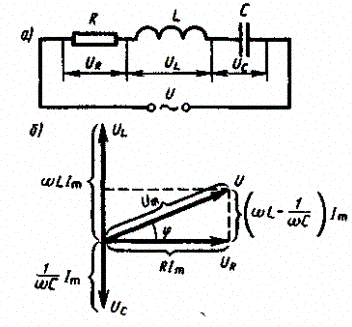
Рис. 216

В цепи возникнет переменный ток, который вызовет на всех элементах цепи соответствующие падения напряжения U_R, U_L и U_c. На рис. 216, б представлена векторная диаграмма амплитуд падений напряжений на резисторе (U_R), катушке (U_L) и конденсаторе (U_C). Амплитуда U_mприложенного напряжения должна быть равна векторной сумме амплитуд этих падений напряжений. Как видно из рис. 216, б, угол jопределяет разность фаз между напряжением и силой тока. Из рисунка следует, что (см. также формулу (147.16))

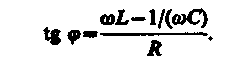(149.9)

Из прямоугольного треугольника получаем

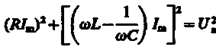
откуда амплитуда силы тока имеет значение

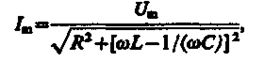(149.10)

совпадающее с (147.15).

Следовательно, если напряжение в цепи изменяется по закону

U = U_mcoswt, то в цепи течет ток

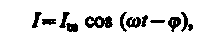(149.11)

где jи I_ш определяются соответственно формулами (149.9) и (149.10). Величина

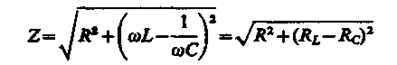(149.12)

называется полным сопротивлением цепи, а величина

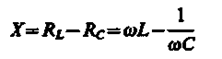
- реактивным сопротивлением.

Рассмотрим частный случай, когда в цепи отсутствует конденсатор. В данном случае падения напряжений U_R и U_L всумме равны приложенному напряжению U. Векторная диаграмма для данного случая представлена на рис. 217, из которого следует, что

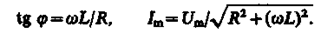(149.13)

Выражения (149.9) и (149.10) совпадают с (149.13), если в них 1/(wС)=0, т. е. С = ¥. Следовательно, отсутствие конденсатора в цепи означает С = ¥, а не С = 0. Данный вывод можно трактовать следующим образом: сближая обкладки конденсатора до их полного соприкосновения, получим цепь, в которой конденсатор отсутствует (расстояние между обкладками стремится к нулю, а емкость — к бесконечности; см. (94.3)).

Рис. 217

Резонанс напряжений

Если в цепи переменного тока, содержащей последовательно включенные конденсатор, катушку индуктивности и резистор (см. рис. 216),

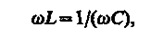(150.1)

то угол сдвига фаз между током и напряжением (149.9) обращается в нуль (j = 0), т. е. изменения тока и напряжения происходят синфазно. Условию (150.1) удовлетворяет частота

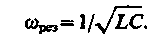(150.2)

В данном случае полное сопротивление цепи Z (149.12) становится минимальным, равным активному сопротивлению Rцепи, и ток в цепи определяется этим сопротивлением, принимая максимальные (возможные при данном U_m)значения. При этом падение напряжения на активном сопротивлении равно внешнему напряжению, приложенному к цепи (U_R = U),а падения напряжений на конденсаторе (U_C) и катушке индуктивности (U_L) одинаковы по амплитуде и противоположны по фазе. Это явление называется резонансом напряжений (последовательным резонансом), а частота (150.2) — резонансной частотой. Векторная диаграмма для резонанса напряжений приведена на рис. 218, а зависимость амплитуды силы тока от wуже была дана на рис. 211.

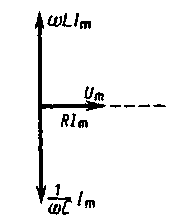
Рис. 218

В случае резонанса напряжений

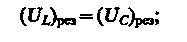
подставив в эту формулу значения резонансной частоты и амплитуды напряжений на катушке индуктивности и конденсаторе, получим

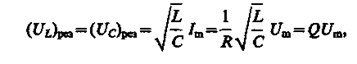
где Q — добротность контура, определяемая выражением (146.14). Так как добротность обычных колебательных контуров больше единицы, то напряжение как на катушке индуктивности, так и на конденсаторе превышает напряжение, приложенное к цепи. Поэтому явление резонанса напряжений используется в технике для усиления колебания напряжения какой-либо определенной частоты. Например, в случае резонанса на конденсаторе можно получить напряжение с амплитудой QU_m (Qв данном случае — добротность контура, которая может быть значительно больше U_m). Это усиление напряжения возможно только для узкого интервала частот вблизи резонанс ной частоты контура, что позволяет выделить из многих сигналов одно колебание определенной частоты, т. е. на радиоприемнике настроиться на нужную длину волны. Явление резонанса напряжений необходимо учитывать при расчете изоляции электрических линий, содержащих конденсаторы и катушки индуктивности, так как иначе может наблюдаться их пробой.

Резонанс токов

Рассмотрим цепь переменного тока, содержащую параллельно включенные конденсатор емкостью Си катушку индуктивностью L (рис. 219).

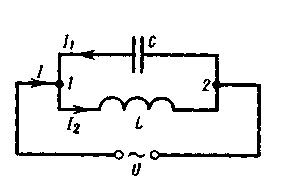
Рис. 219

Для простоты допустим, что активное сопротивление обеих ветвей настолько мало, что им можно пренебречь. Если приложенное напряжение изменяется по закону U = U_mcoswt (см. (149.1)), то, согласно формуле (149.11), в ветви 1С2течет ток

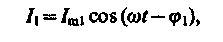
амплитуда которого определяется из выражения (149.10) при условии R = 0 и L = 0:

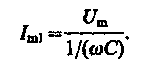
Начальная фаза j₁ этого тока по формуле (149.9) определяется равенством

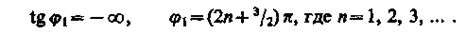(151.1)

Аналогично, сила тока в ветви 1L2

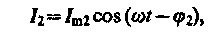
амплитуда которого определяется из (149.10) при условии R = 0 и С = ¥ (условие отсутствия емкости в цепи, см. § 149):

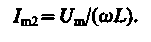
Начальная фаза j₂ этого тока (см. (149.9))

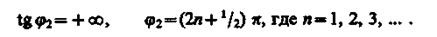(151.2)

Из сравнения выражений (151.1) и (131.2) вытекает, что разность фаз токов в ветвях 1С2 и 1L2равна j₁ - j₂ = p, т. е. токи в ветвях противоположны по фазе. Амплитуда силы тока во внешней (неразветвленной) цепи

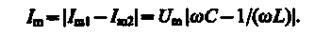
Если w = w_рез = 1/ÖLC, то I_m1 = I_m2 и I_m = 0. Явление резкого уменьшения амплитуды силы тока во внешней цепи, питающей параллельно включенные конденсатор и катушку индуктивности, при приближении частоты со приложенного напряжения к резонанс ной частоте соре, называется резонансом токов (параллельным резонансом). В данном случае для резонансной частоты получили такое же значение, как и при резонансе напряжений (см. § 150).

Амплитуда силы тока I_m оказалась равна нулю потому, что активным сопротивлением контура пренебрегли. Если учесть сопротивление R, то разность фаз j₁ - j₂ не будет равна p, поэтому при резонансе токов амплитуда силы тока I_m будет отлична от нуля, но примет наименьшее возможное значение. Таким образом, при резонансе токов во внешней цепи токи I₁и I₂ компенсируются и сила тока I в подводящих проводах достигает минимального значения, обусловленного только током через резистор. При резонансе токов силы токов I₁ и I₂ могут значительно превышать силу тока I.

Рассмотренный контур оказывает большое сопротивление переменному току с частотой, близкой к резонансной. Поэтому это свойство резонанса токов используется в резонансных усилителях, позволяющих выделять одно определенное колебание из сигнала сложной формы. Кроме того, резонанс токов используется в индукционных печах, где нагревание металлов производится вихревыми токами (см. § 125). В них емкость конденсатора, включенного параллельно нагревательной катушке, подбирается так, чтобы при частоте генератора получился резонанс токов, в результате чего сила тока через нагревательную катушку будет гораздо больше, чем сила тока в подводящих проводах.