Закон Ома для участка цепи

Направленное движение электрических зарядов под действием сил электрического поля называют электрическим током.

Ток может идти в твердых телах, жидкостях и газах. Если среда является проводником с большим количеством свободных электронов, то течение электрического тока осуществляется за счет дрейфа этих электронов. Различают ток проводимости (упорядоченное движение электронов в проводниках, ионов в электролитах, электронов и дырок в полупроводниках, ионов и электронов в газах) и конвекционный ток (упорядоченное перемещение электрических зарядов, связанное с перемещением заряженного тела в пространстве).

За направление тока принят дрейф положительных зарядов (электроны проводимости всегда движутся в направлении, противоположном направлению тока). Количественной характеристикой электрического тока являются сила тока I и плотность тока j.

Сила тока – скалярная величина, равная отношению количества электричества dq, которое за время dt переносится через данное сечение проводника, ко времени dt: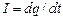

Постоянным током называют электрический ток, сила и направление которого с течением времени не изменяются. Для постоянного тока:

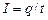
Единица силы электрического тока – ампер (А).

Плотность тока – векторная физическая величина, модуль которой равен отношению силы тока I к площади поперечного сечения проводника S: 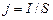. Вектор 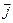направлен вдоль направления тока, т.е. совпадает с направлением упорядоченного движения положительных зарядов.

Единица плотности электрического тока – А/м².

Прохождение электрического тока проявляется по следующим признакам: 1) по действию на магнитную стрелку, помещенную вблизи проводника; 2) по термическому действию – при прохождении тока проводник нагревается; 3) по химическому действию (электролиз–выделение составляющих сложных соединений с помощью тока).

Для того чтобы в проводнике все время шел ток, необходимо поддерживать в нем постоянное электрическое поле. Возьмем металлический проводник длиной l. Пусть Е – напряженность электрического поля внутри проводника, а j₁ – j₂=U – постоянная разность потенциалов на концах проводника. Тогда: .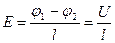

Г.Ом экспериментально установил, что сила тока в металлических проводниках пропорциональна приложенному напряжению:

I = GU.

Коэффициент пропорциональности G называют электропроводимостью проводника, а обратную величину R = G^-1 – его электрическим сопротивлением.

Закон Ома для участка цепи: сила тока в проводнике пропорциональна напряжению на его концах и обратно пропорциональна сопротивлению проводника:

.

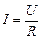Единица сопротивления – ом (Ом).

Электрическое сопротивление обусловлено тем, что свободные электроны при дрейфе взаимодействуют с положительными ионами кристаллической решетки металла. При повышении температуры учащаются соударения электронов с ионами, поэтому сопротивление проводников зависит от температуры: R=R₀ (1+ at),где R₀ - сопротивление при 0^оС, R - сопротивление при t^oC, a - термический коэффициент сопротивления. Для всех чистых металлов а ~ 1/273 К^–1 . Зависимость сопротивления металлов от температуры положена в основу устройства термометров сопротивления. Они используются как при очень высокой, так и при очень низкой температуре, когда применение жидкостных термометров невозможно.

Сопротивление проводников зависит также от материала проводника, т. е. строения его кристаллической решетки. Для однородного цилиндрического проводника длиной l и площадью поперечного сечения S сопротивление определяется по формуле:

R= ,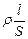

где r=RS/1 – удельное сопротивление проводника (сопротивление однородного цилиндрического проводника, имеющего единичную длину и единичную площадь поперечного сечения).

Единица удельного сопротивления – ом-метр (Ом×м).

Величина 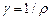, обратная удельному сопротивлению, называется удельной электрической проводимостью проводника. Единица электрической проводимости – сименс (См). Сименс – электрическая проводимость проводника сопротивлением 1 Ом; 1 См=1 Ом^-1.

Закон Ома можно представить в дифференциальной форме:

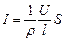или 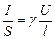. Тогда: j = gE.

Направления векторов j и Е совпадают, так как носители заряда в каждой точке движутся в направлении вектора Е. Следовательно, этот закон можно переписать в виде:

.

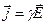Это закон Ома в дифференциальной форме.

Соединения проводников.