Числовые характеристики случайных сигналов

При исследовании случайных процессов в качестве их числовых характеристик используются смешанные начальные и центральные моменты. Из них наиболее широко используются моменты распределения первых двух порядков: математическое ожидание, дисперсия и корреляционная функция случайного процесса.

а) Математическое ожидание (или первый момент одномерного закона распределения) выражается формулой

.

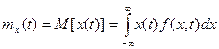(1.23)

В общем случае 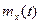зависит от времени и физически выражает среднее значение совокупности выборок случайного процесса в определенный момент времени.

В частном случае 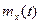может быть постоянной величиной

.

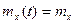б) Дисперсия (или второй центральный момент) – это математическое ожидание квадрата отклонения величин х(t) от математического ожидания

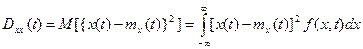. (1.24)

Дисперсия выражает меру разброса значений случайной величины х(t₁) около математического ожидания, т.е. «степень случайности» величины х(t₁).

Корень квадратный из дисперсии принято называть среднеквадратическим отклонением (средним квадратичным отклонением) случайной величины.

.

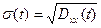(1.25)

Можно определить второй начальный момент, как математическое ожидание квадрата случайной величины х(t)

.

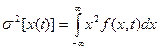(1.26)

Связь между начальными и центральными моментами случайных величин устанавливается следующим соотношением

,

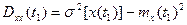(1.27)

т.е. дисперсия равна разности квадратов среднеквадратического значения случайной функции и ее математического ожидания.

При дисперсия совпадает с .

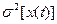Рассмотренные характеристики описывают поведение случайного процесса в отдельные моменты времени, но совершенно не затрагивают связь между значениями случайного процесса в различные моменты времени.

в) Эту связь выражает корреляционная функция 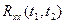, определяемая как математическое ожидание произведения центрированных значений случайной функции х(t) в моменты времени и .

,

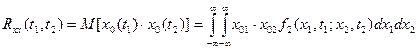(1.28)

где .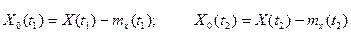

В некоторых случаях 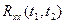называется автокорреляционной функцией, в отличие от 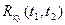, устанавливающей связь между двумя случайными процессами и 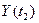и называемой взаимнокорреляционной функцией.

Иногда рассматривают нормированную автокорреляционную 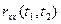функцию (коэффициент корреляции), определяемую выражением

.

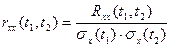Нормированные корреляционные функции изменяются в пределах [0; 1].

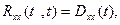При = =t а 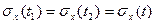, следовательно

.

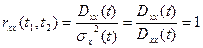Этот случай соответствует полной связанности (коррелированности) и 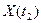. В этом случае, когда и 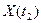полностью не связаны, то 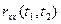=0.

г) Определение числовых характеристик путем усреднения во времени (эргодичность процессов)

Рассмотренные числовые характеристики могут быть получены путем усреднения во времени (обработкой одной из реализаций случайного процесса на достаточно большом интервале времени).

Среднее по времени значение случайного процесса определяется выражением

,

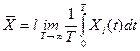(1.29)

где 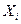(t) – реализация процесса, 2T – время наблюдения;

По аналогии пользуются понятиями среднего по времени значения от функции 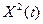, от квадрата разности 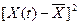и от произведения 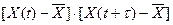, определяемыми соответственно выражениями

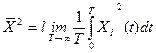,	(1.30)
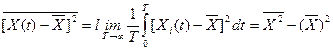,	(1.31)
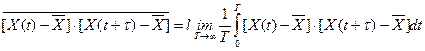,	(1.32)

Для различных реализаций получаются различные значения по формулам (1.29-1.32).

Если предположить, что X(t) – изменение тока или напряжения, то физически квадрат значения 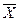определяет мощность постоянной составляющей, рассеиваемой на сопротивлении 1 Ом. По аналогии можно считать, что (1.30) определяет полную среднюю мощность, а (1.31) выражает среднюю мощность «случайной» составляющей процесса.

Если случайный сигнал является дискретным, то числовые характеристики определяются выражениями

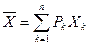	(1.33)
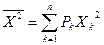	(1.34)
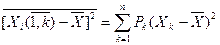	(1.35)
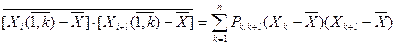,	(1.36)

где 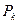- априорная вероятность случайной величины ;

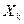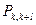- совместная априорная вероятность величин 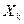и ;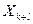

n – число значений величины X.