Магнитное напряжение зубцов

t₁=b_п1+b_z1– зубцовое деление

Магнитный поток входит в якорь по двум параллельным путям, через зубцы и пазы. На протяжении полюса все зубцы в магнитном поле находятся в одинаковых условиях, поэтому для расчета можно рассматривать одно зубцовое деление. Для сечения на расстоянии х от поверхности якоря

Ф_t=Ф_zx+Ф_пх

где Ф_{t_}– поток на одно зубцовое деление;

Ф_zx– поток зубца в данном сечении;

Ф_пх– поток в пазу в том же сечении.

Поток на одно зубцовое деление

Ф_t=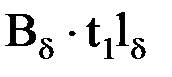

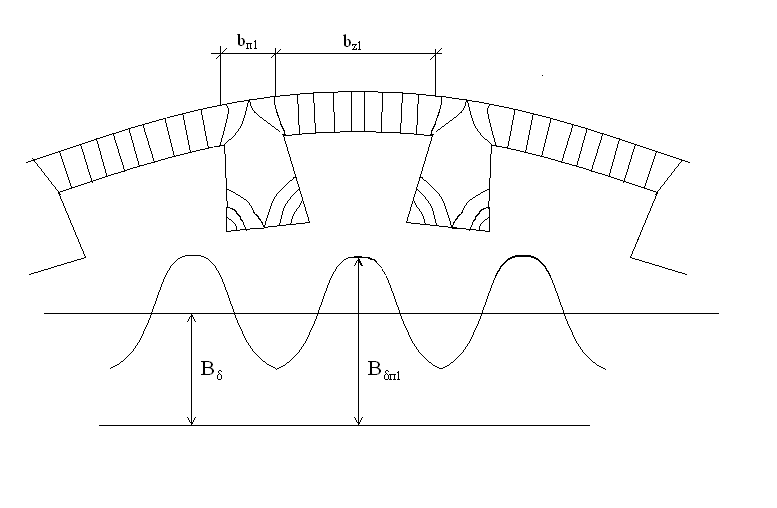
Распределение Ф_t между зубцом и пазом происходит обратно пропорционально их магнитным сопротивлениям. Если сталь зубца не насыщена, то его магнитное сопротивление во много раз меньше, чем магнитное сопротивление паза, поэтому можно считать, что весь поток идет через зубец

Ф_t=Ф_zx= .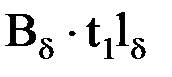

Разделим это уравнение на площадь зубца в сечении х

B_zx= ,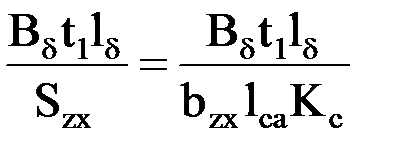

где В_zx= 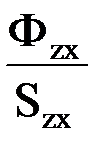– индукция в сечении х зубца;

S_zx=b_zxl_caK_c– площадь зубца в том же сечении;

К_с – коэффициент заполнения пакетов сталью( учитывает изоляцию между листами), К_с= 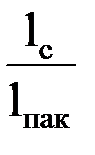, где l_c– длина чистой стали в пакете; 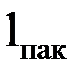–длина пакета.

Обычно К_с=0,91…0,93.

Для определения напряженности магнитного поля в зубце Н_zx используется кривая намагничивания стали В=f(H), из которой сделан сердечник якоря. Для сердечников современных ЭМ используется холоднокатаная изотропная электротехническая сталь марок 2013, 2312, 2411.

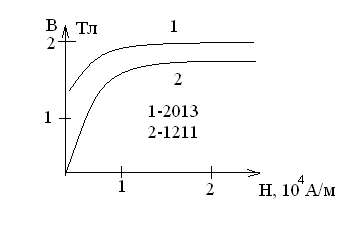Ранее применялась горячекатаная сталь марок 1211, 1212, 1311, 1411 и др.

Магнитную индукцию В_zx можно определять по формуле до В_zx≤1,8 Тл. При больших значениях Вzx>1.8 Тл происходит насыщение стали зубца, его магнитное сопротивление возрастает и часть потока вытесняется в паз. В этом случае индукция в зубце определяется по формуле Ф_t=Ф_zx+Ф_пх.

Поделим это уравнение на площадь зубца S_zx в сечении х

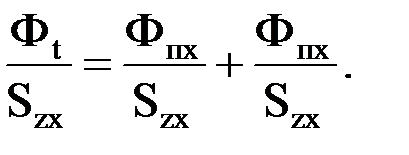
Величина 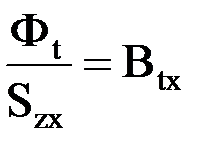называется расчетной индукцией в сечении зубца. Первое слагаемое – действительная индукция В_zx в том же сечении. Второе слагаемое можно представить

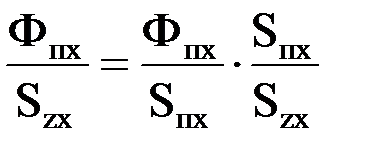=В_пхК_пх= ,

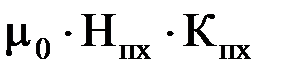где S_пх, В_пх– площадь паза и индукция в сечении х;

Н_пх – напряженность магнитного поля;

К_пх– коэффициент определяемый размерами паза и зубца в сечении х.

Пазы и зубцы в сечении х находятся на одном уровне, поэтому Н_zx=H_пх. Тогда

В_tx=B_zx+ .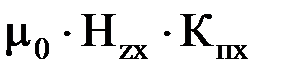

Это нелинейное уравнение, запишем его в виде

В_zx=B_tx– ,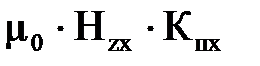

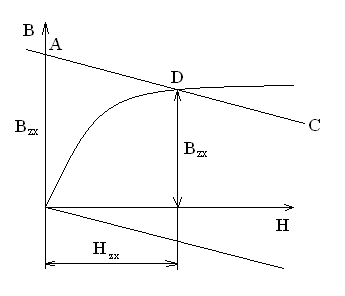И воспользуемся графическим решением. Строится кривая намагничивания В=f(H).Для сечения х зубца определяется расчетная индукция В_zx= 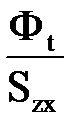и откладывается на оси ординат. Из точки проводится прямая АС, ординат которой равны B_tx– 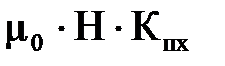. Пересечение прямой Ас с кривой намагничивания дает значение действительной индукции в зубце В_zx и соответствующую ей напряженность магнитного поля .

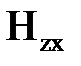В пособиях по проектированию ЭМ приводится зависимость В_t=f(H_z) при различных значениях К_п .По расчетной индукции В_tx можно определить напряженность .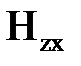

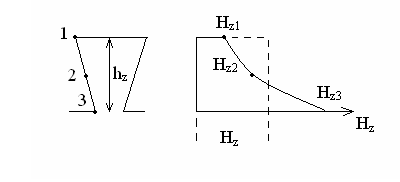Трапециидальная форма зубца. Площадь сечения по высоте зубца изменяется. Индукция тоже изменяется. Напряженность тоже. Чтобы определить расчетное значение Н_z проводится расчет для ряда точек по высоте зубца (обычно три точки в верхнем, нижнем и среднем сечении).Для каждого сечения определяется расчетная индукция B_tx, а по ней напряженность определяется непосредственно по кривой намагничивания стали. При В_zx >1,8 Тл – по одной из кривых, подобных тем, какие приводятся в пособиях по расчету ЭМ(требуемая кривая выбирается по коэффициенту К_пх). По полученным данным строится кривая изменения 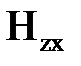по высоте зубца. Среднее значение Н_z определяется путем интегрирования кривой распределения 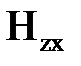по высоте зубца. Приближенная формула интегрирования (Симпсона) имеет вид

Н_z=( Н_z1 +4 Н_z2 + Н_z3) .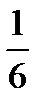

Магнитное напряжение зубца

F_z=2H_zh_z.

Иногда используется формула

F_z=2H_{Z 1/3} h_z,

где H_{Z 1/3} – напряженность поля на расстоянии 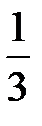h_z от основания зубца.

Овальные пазы

Большую часть на высоте зубцы имеют одинаковое сечение. Можно принять, что B_zx по высоте зубца остается постоянной и H_zx=H_z и определяется для одного среднего сечения.

Если полюсные наконечники имеют зубчатое строение, то эта часть магнитной цепи рассчитывается аналогично зубцовой зоне якоря.