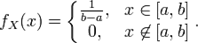Случайные процессы и их осн. хар-ки
Случайный процесс Х(t)—это особого вида функция, характеризующаяся тем, что в любой момент времени t принимаемые ею значения являются случайными величинами. Случайность процесса X(t) проявляется в том, что вид наблюдаемой функции случайным образом меняется от одного наблюдения к другому. Однако получаемая в результате каждого отдельного опыта функция х(t) не случайна, её называют реализацией случайной функции. Случайный процесс представляет собой бесконечную совокупность таких реализации, образующих статистический ансамбль.
Для непрерывных процессов X(t) распределение вероятностей в заданном сечении t1 характеризуется одномерной плотностью вероятностей:
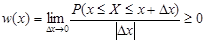
Другой важной характеристикой случайных величин Х является интегральная функция распределения F(x), определяемая как вероятность того, что случайная величина X не превзойдёт некоторого значения х: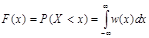 
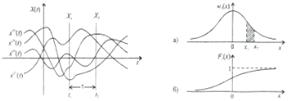
Рис.1. Задание случайного процесса через совокупность его реализаций Рис. 2. Типовой график (а) одномерной ПВ и (б) одномерной ИФР
Случайными стационарными процессамипринято называть случайные процессы, статистические характеристики которых одинаковы во всех сечениях.
Если же мат.ожидание т и дисперсия σ2 процесса не зависят от времени, а функция корреляции зависит лишь от разности τ=|t2-t1|, т.е. R(t1,t2)=R(τ), то подобный случайный процесс будет стационарен в широком смысле. Как следует из определения, функция корреляции стационарного случайного процесса является четной. R(τ)=R(-τ).
Случайный стационарный процесс называют эргодическим, если при нахождении его моментных функций усреднение по статистическому ансамблю можно заменить усреднением по времени. Операция усреднения выполняется над единственной реализацией х(t), длительность Т которой теоретически может быть сколь угодно велика.
Функция Wx(ω) наз-ся спектральной плотностью мощностиили спектром мощности процесса X(t).Спектр мощности связан преобразованием Фурье с функцией корреляции. W(ω)=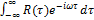 
. Характеризует удельную меру мощности. По своему физ.смыслу спектр мощности веществен и неотрицателен: W(ω)≥0.
Т-ма Винера-Хинчина:
Спектр плотности W(ω)= 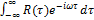и функция корреляции R(τ)= 
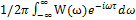связаны между собой.
Случайный процесс, характеризуемый спектральной плотностью мощности G0(f)=N0 равномерной на всех частотах? Называют белым шумом. Если спектр G0(f) ограничен сверху частотой Fв, то процесс наз-ся квазибелым шумом. Его дисперсия Ϭ2=B(0)=N0FB. ФК белого шума: B(τ)=δ(τ)*N0/2. ФК квазибелого шума: B(τ)=N0FB(sinωвτ/ωвτ).
Нормальное распределение — распределение вероятностей, которое задается функцией плотности распределения: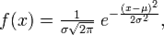 
где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия.
случайная величина имеет непрерывное равномерное распределение на отрезке [a,b], если её плотность имеет вид:
