Скорость передачи информации и

Пропускная способность канала связи

Ввиду того, что канал связи считается стационарным, на вход канала поступает последовательность символов 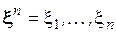, где каждый символ 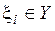, образует n-разрядный код. Количество комбинаций, которое можно образовать с использованием кода с основанием D, равно 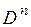. Множество этих комбинаций образует пространство значений кодовых комбинаций 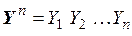. Символы при ансамбле Y обозначают моменты времени реализации величины 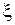. Например, для двумерного ансамбля c основанием кода, равным D=3, имеем

.

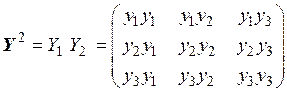На выходе канала имеем последовательность символов 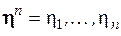, где каждый символ 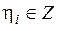. Точно так же можно образовать множество кодовых комбинаций, составляющих пространство .

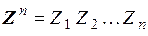Последовательность символов 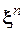поступает в канал в течение .

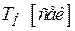Количество информации, которое передается по каналу связи, за время наблюдения 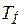согласно (1.18) равно

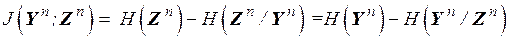. (4.2)

Скоростью передачи информации по каналу связи называется величина

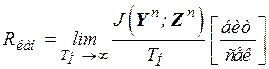. (4.3)

Скорость передачи информации R отражает среднюю скорость передачи информации в единицу времени.

Максимальная скорость передачи информации 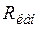называется пропускной способностью канала связи

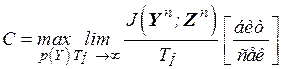. (4.4)

Рассмотрим в выражении (1.18) разность 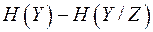. Чем больше энтропия 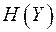, тем больше пропускная способность канала связи. Величина 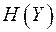определяет среднюю неопределённость, содержащуюся в ансамбле Y, которая зависит от распределения вероятности элементов ансамбля Y. Поэтому максимизация скорости передачи информации происходит по распределению вероятности элементов ансамбля Y.

Упростим выражение (4.2).

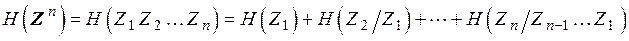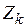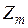. В силу того, что канал - стационарный и реализации элементов ансамблей и в моменты времен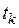и и 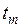независимы. Тогда

.

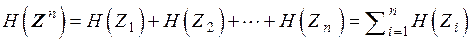Но ансамбли 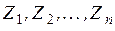за время передачи информации неизменны, т.е. 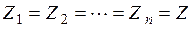. Тогда имеем

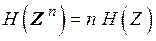(4.5)

Условная энтропия в (4.2) представляется как

= =

= .

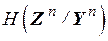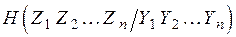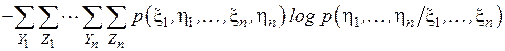Воспользуемся условием независимости символов попарно на входе и выходе канала связи, а также стационарностью канала. Тогда соответствующие вероятности и условная энтропия будут равны

= ,

= ,

= =

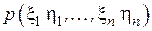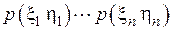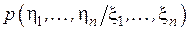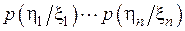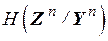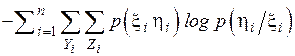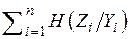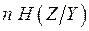= = . (4.6)

Если отсчёты во времени эквидистантны, то 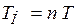, где 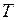- интервал дискретизации по времени. Подставив (4.5), (4.6) и 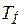в (4.4), получим

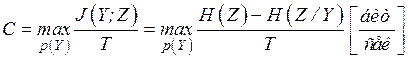. (4.7)

Введём скорость передачи символов

.

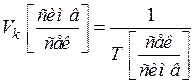Тогда пропускную способность можно записать как

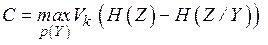(4.8)

В таблице 4.1 представлены характеристики источника сообщений, кодера источника и канала связи.

Таблица 4.1

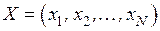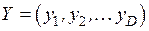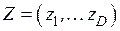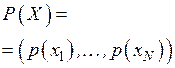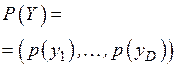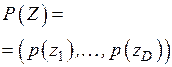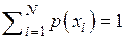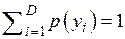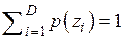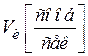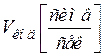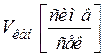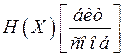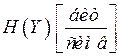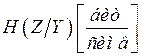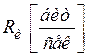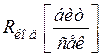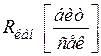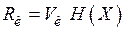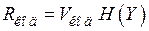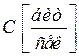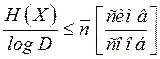Канал без шумов

Шум в канале связи искажает физические параметры сигнала, что в свою очередь приводит к искажению символов. Вероятностная характеристика искажений – это условная вероятность 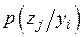. Будем считать, сигнал в канале не искажается, если 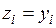. Тогда для канала без шумов справедливо выражение

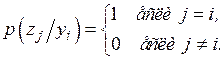(4.9)

Из выражения (**.9) следует, 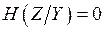, т.е. пропускная способность канала связи равна

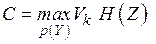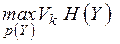= (4.10)

Если используется код с основанием D ,то энтропия ансамбля 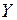достигает наибольшего значения при 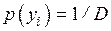. Тогда пропускная способность канала равна

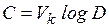. (4.11)

Теорема Шеннона о кодирование источника независимых сообщений для канала без шумов. (Шеннон, стр. 270)

Пусть источник имеет энтропию 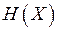, а канал имеет пропускную способность 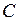. Тогда можно закодировать сообщения таким образом, что можно передавать их со средней скоростью

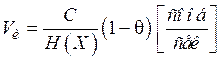, где .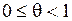

Передавать сообщения со скоростью большей, чем 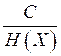, невозможно.

Доказательство. Будем считать источник сообщений согласованным с каналом по скорости передачи информации, если 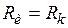. Тогда

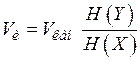. (4.12)

Энтропия 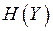не превышает 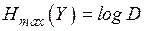. Запишем

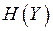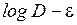= ,. (4.13)

где .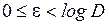

Подстановка (4.13) в (4.12) позволяет получить

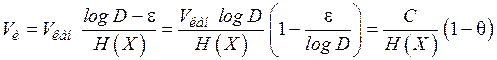, (4.14)

где .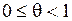

Если принять 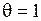, то 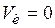, т.е. не имеет смысла передавать сообщения.

Канал с шумами

Наличие шума в канале связи приводит к тому, что условная энтропия 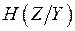не равна нулю. Условную энтропию 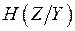Шеннон назвал ненадёжностью канала, так как она зависит от шума в канале связи. В результате возникает вопрос, существует ли метод кодирования, позволяющий передавать информацию с определённой скоростью 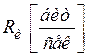. На это вопрос отвечает теорема Шеннона (Шеннон стр.280).

Пусть дискретный канал обладает пропускной способностью 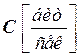, а дискретный источник – энтропией 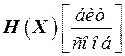. Если 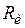< 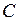, то существует такая система кодирования, что сообщения источника могут быть переданы по каналу с произвольно малой частотой ошибок, (или со сколь угодно малой энтропией 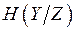). Если 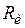> 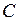, то можно закодировать источник таким образом, что ненадёжность 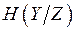канала будет меньше, чем 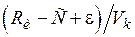, где 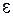сколь угодно мало. Не существует способа кодирования, обеспечивающего ненадёжность, меньшую, чем .

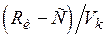Нет доказательства

Пример 4.1. Определим пропускную способность двоичного симметричного канала связи. Модель двоичного симметричного канала показан на рисунке 4.4.

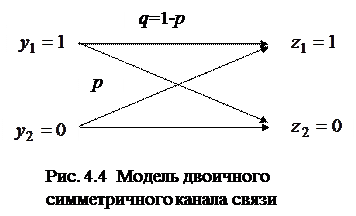В канал связи поступают символы 1 и 0, отображающие реальные физические сигналы.

1) Канал симметричный. Вероятности искажения символов равны 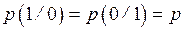, вероятности неискажённого приема символов равны .

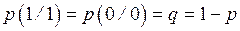2) Канал стационарный, так как условные вероятности не зависят от времени.

Пропускную способность вычислим по формуле (4.8). Энтропию 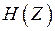определим из условия 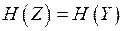при отсутствии шума. Энтропия 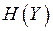принимает максимальное значение, равное 1, при 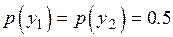. Условная энтропия равна

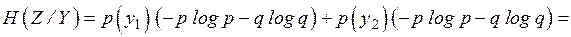
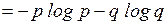
Подставляя полученные величины в (4.8), получим

.

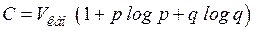Как видно из формулы, пропускная способность зависит скорости поступления символов в канал и от вероятности искажения символов.

Положим, задан ансамбль сообщений X с распределением вероятностей P , (Таблица 4.2) . Сообщения генерируются со скоростью 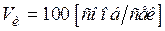.Способ кодирования определён и каждому сообщению приписан двоичный код. Энтропия ансамбля сообщений X равна ,

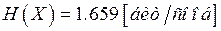Таблица 4.2
X	P	код
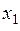	0.6
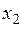	0.2
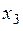	0.1
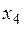	0.07
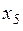	0.03

вероятности реализации символов «1» и «0» равны

,

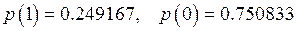энтропия ансамбля символов Y равна

,

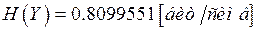средняя длина кода равна .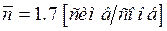

Положим, в канале действует такой шум, что вероятность ошибочного перехода равна 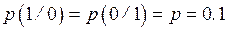. Сможет ли канал обеспечить передачу сообщений ?

1)

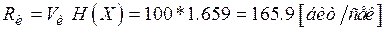
2) Будем считать 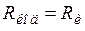. Тогда 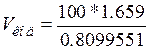= 204.826 .

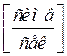3) Будем считать 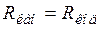. Тогда 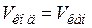и пропускная способность канала равна =

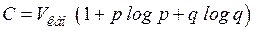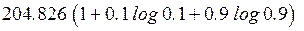= = 108.764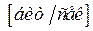

Как видно, пропускная способность канала значительно ниже скорости генерации информации источником и часть информации может быть утеряна. В этом случае можно уменьшить скорость генерации сообщений 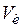или уменьшить вероятность ошибок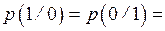 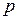. Положим, каким-то образом удалось уменьшить вероятности ошибок до величины 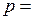0.01. Тогда пропускная способность канала увеличится до величины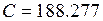 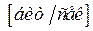. При таком соотношении скорости поступления информации 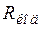в канал и пропускной способности канала искажения информации в канале из-за величин 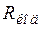и 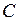не будет.

Непрерывный канал связи

Как и прежде, сигналы поступают в канал в дискретные моменты времени, но значения сигналов принимают непрерывные значения из некоторого множества. Примером такого канала является передача амплитудно-модулированных, фазомодулированных или частотно-модулированных сигналов. Сами сигналы могут быть как детерминированными, так и являться случайными процессами. Сигнал и шум взаимно независимы и в канале связи складываются алгебраически, т.е сигнал и шум аддитивны

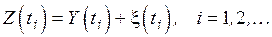, (4.15)

где 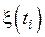- шум в канале с известной плотностью вероятности ,

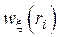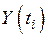- непрерывный по множеству значений сигнал, поступающий в канал связи. Плотность распределения вероятности 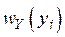значений сигнала может быть произвольной

Чтобы упростить записи, в дальнейшем будем писать

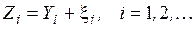, (4.16)

помня, что 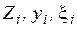- непрерывные величины, а их реализациями являются 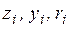. Запишем равенство (4.16) через реализации

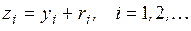(4.17)

Условная плотность распределения 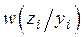при фиксированном значении 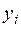должна удовлетворять соотношению

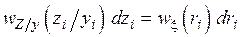. (4.18)

Используя (**.17), получим условную плотность распределения

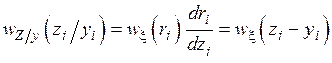(4.19)

Пропускная способность непрерывного канала связи определяется подобным образом, что и для дискретного канала, но максимизация пропускной способности производится по всем возможным распределениям :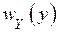

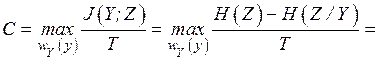
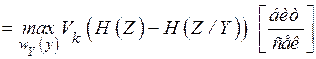, (4.20)

где 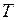- время, затраченное на передачу одного значения ,

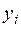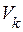- скорость передачи сигналов в канале - количество значений 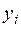, переданных по каналу в единицу времени.

Определим условную энтропию :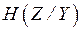

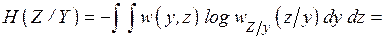
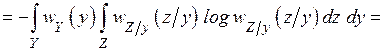
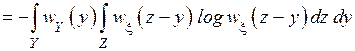(4.21)

Из (4.21) видно, что условная энтропия 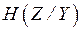зависит от плотности распределения вероятности шума.

Пример 4.3. Вычислим энтропию случайной величины 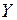, подчиненной нормальному закону с математическим ожиданием, равным m, и дисперсией, равной .

=

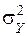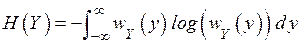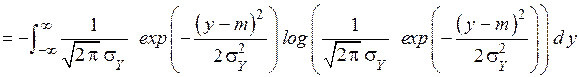
Сделаем замену переменных .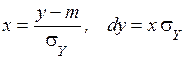

.

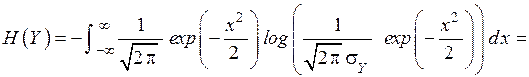
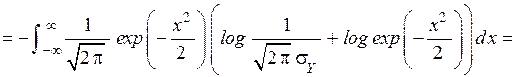
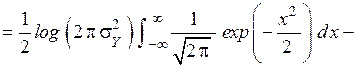
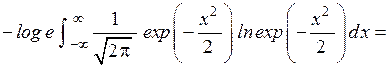
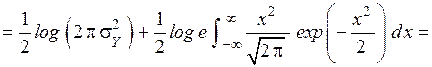
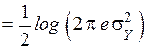Как видно, энтропия 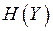не зависит от математического ожидания m.

Пусть 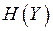- энтропия случайной величины 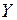с математическим ожиданием, равным нулю, и дисперсией, равной 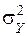. Энтропия случайной величины 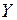не превышает энтропии нормального закона распределения вероятности

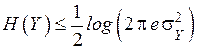,(4.22)

где знак равенства имеет место тогда и только тогда, когда случайная величина 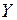распределена по нормальному закону.

Положим, 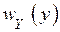- произвольная плотность распределения вероятности случайной величины 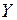. Случайная величина подвергается преобразованию

.

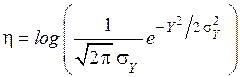Определим математическое ожидание случайной величины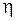

=

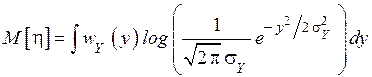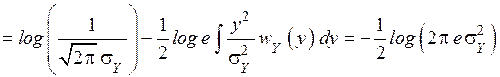. (4.23)

Рассмотрим разность 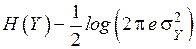. Правая часть этой разности есть 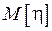. Поэтому

.

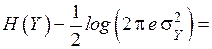
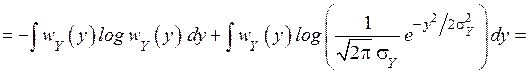
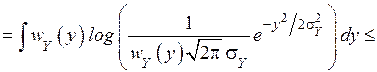
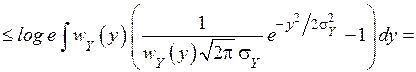
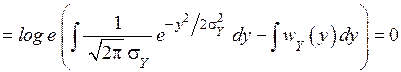Знак равенства будет только тогда, когда справедливо равенство

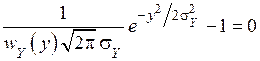или

.

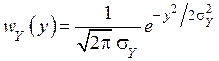Таким образом, энтропия достигает максимального значения при нормальном законе распределения вероятности. При этом накладываются условия:

- дисперсия 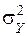случайной величины ограничена,

- область определения плотности распределения вероятности – ( ).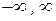

При рассмотрении пропускной способности канала связи никаких ограничений на вид распределения вероятности шума не накладывалось. В частном случае, наиболее употребляемом на практике, предполагается, что шум - нормальный белый. Это означает, что значения шума распределены по нормальному закону и они не коррелированны. При таких предположениях имеет место теорема Шеннона (Фано, стр. 176)

Если в непрерывном постоянном канале с дискретным временем аддитивный шум имеет гауссовское распределение с нулевым средним и дисперсией, равной 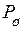, а мощность сигнала на входе не может превышать определенной величины 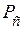, то пропускная способность этого канала на событие определяется формулой

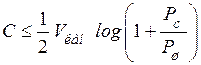.(4.24)

Знак равенства достигается лишь тогда, когда сигнал на входе канала - гауссовский с нулевым средним и дисперсией, равной .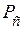

Как известно, пропускная способность канала имеет вид

.

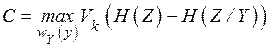Определим 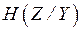. Из соотношений (4.15) - (4.18) следует,

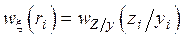. В силу независимости сигнала и шума .

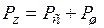По определению

.

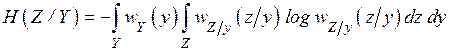Подставим вместо условной плотности 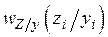плотность распределения шума и, учитывая, что шум распределён по нормальному закону, получим

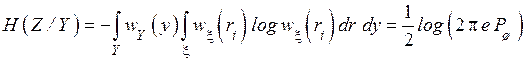. (4.25)

Используя общее определение пропускной способности канала (4..20)

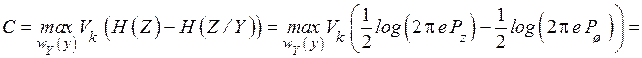
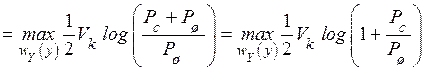. (4.25)

Если сигнал на входе канала распределен по нормальному закону, то и сумма (4.16) также распределена по нормальному закону, что является необходимым условием максимального значения энтропии 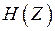. В этом случае пропускная способность достигает максимального значения (знак равенства в (4.24)).