Спектральная плотн. неинтегрируемых сигналов. об форм релея
Математические модели многих сигналов, широко применяемых в радиотехнике, не удовлетворяют условию абсолютной интегрируемости, поэтому метод преобразований Фурье в обычном виде к ним неприменим. Однако можно говорить о спектральных плотностях таких сигналов, если допустить, что эти плотности описываются обобщенными функциями.
Пусть два сигнала и(t) и v(t), в общем случае комплексно-значные, определены своими обратными преобразованиямиФурье.
Найдем скалярное произведение этих сигналов, выразив один из них, например v(t), через его спектральную плотность :
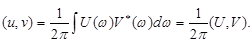
Полученное соотношение представляет собой обобщенную формулу Рэлея. Легко запоминающаяся трактовка этой формулы такова: скалярное произведение двух сигналов с точностью до коэффициента пропорционально скалярному произведению их спектральных плотностей.Если сигналы тождественно совпадают, то скалярное произведение становится равным энергии
.
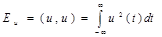Назовем взаимным энергетическим спектром вещественных сигналов u(t) и v(t) функцию
,
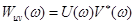такую, что
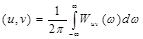
Спектральное представление энергии сигнала легко получить из обобщенной формулы Рэлея, если в ней сигналы и(t) и v(t) считать одинаковыми. Формула (4.8), выражающая спектральную плотность энергии, приобретает вид
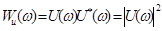. (4.11)
Величина Wu(ω) носит название спектральной плотности энергии сигнала и(t), или, короче, его энергетического спектра. Формула (3.2) при этом запишется так: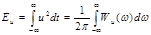 
.
Соотношение (4.12) известно как формула Рэлея (в узком смысле), которая констатирует следующее: энергия любого сигнала есть результат суммирования вкладов от различных интервалов частотной оси.