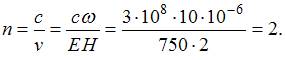Энергия волны. Перенос энергии волной

4.4.1. В упругой среде плотностью ρ распространяется плоская синусоидальная волна. Если амплитуда волны увеличится в 4 раза, а частота в 2 раза, то плотность потока энергии (вектор Умова) увеличится в ______ раз(-а).

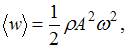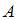Решение:Плотность потока энергии, то есть количество энергии, переносимой волной за единицу времени через единицу площади площадки, расположенной перпендикулярно направлению переноса энергии, равна: U=w∙v где w– объемная плотность энергии, v – скорость переноса энергии волной (для синусоидальной волны эта скорость равна фазовой скорости). Среднее значение объемной плотности энергии равно: где – амплитуда волны, 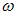– частота. Следовательно, плотность потока энергии увеличится в 64 раза.

4.4.2. Плотность потока энергии, переносимой волной в упругой среде плотностью ρ, увеличилась в 16 раз при неизменной скорости и частоте волны. При этом амплитуда волны возросла в _____ раз(а).

Решение:Плотность потока энергии, то есть количество энергии, переносимой волной за единицу времени через единицу площади площадки, расположенной перпендикулярно направлению переноса энергии, равна: U=w∙v где w – объемная плотность энергии, v – скорость переноса энергии волной (для синусоидальной волны эта скорость равна фазовой скорости). 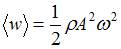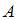Среднее значение объемной плотности энергии равно: , где – амплитуда волны, 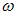– частота. Следовательно, амплитуда увеличилась в 4 раза.

4.4.3. Если частоту упругой волны увеличить в 2 раза, не изменяя ее скорости, то интенсивность волны увеличится в ___ раз(-а).

Решение:Интенсивностью волны называется скалярная величина, равная модулю среднего значения вектора плотности потока энергии (вектора Умова) 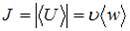, где 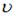– скорость волны, 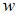– объемная плотность ее энергии. Среднее значение объемной плотности энергии упругой волны определяется выражением 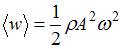, где ρ – плотность среды, 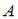– амплитуда, 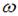– циклическая частота волны. Тогда интенсивность волны равна 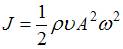. Таким образом, если частоту упругой волны увеличить в 2 раза, не изменяя ее скорости, то интенсивность волны увеличится в 4 раза.

4.4.4. В физиотерапии используется ультразвук частотой 800 кГц и интенсивностью 1 Вт/м². При воздействии таким ультразвуком на мягкие ткани человека плотностью 1060 кг/м³ амплитуда колебаний молекул будет равна …

(Считать скорость ультразвуковых волн в теле человека равной 1500 м/с. Ответ выразите в ангстремах (1 Ǻ=10^-10 м) и округлите до целого числа.)

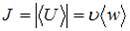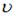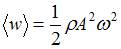Решение:Интенсивностью волны называется скалярная величина, равная модулю среднего значения вектора плотности потока энергии (вектора Умова) , где – скорость волны, – объемная плотность ее энергии. Среднее значение объемной плотности энергии упругой волны определяется выражением , где 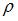– плотность среды, 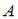– амплитуда, 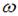– циклическая частота волны. Тогда интенсивность волны равна .

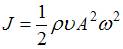Отсюда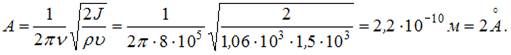

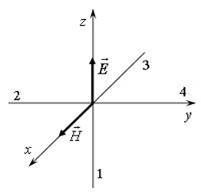4.4.5. На рисунке показана ориентация векторов напряженности электрического ( 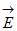) и магнитного ( 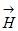) полей в электромагнитной волне. Вектор плотности потока энергии электромагнитного поля ориентирован в направлении …

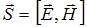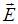Решение:Вектор плотности потока энергии электромагнитного поля (вектор Умова – Пойнтинга) равен векторному произведению: , где и 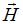– соответственно векторы напряженностей электрического и магнитного полей электромагнитной волны. Векторы 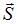, , 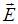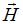образуют правую тройку векторов; значит, вектор Умова – Пойнтинга ориентирован в направлении 4.

4.4.6. Если в электромагнитной волне, распространяющейся в вакууме, значение напряженности магнитного поля равно: Н=10 А/м, объемная плотность энергии ω=10^-5 Дж/м³, то напряженность электрического поля составляет _____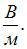

Решение:Плотность потока энергии электромагнитной волны (вектор Умова – Пойнтинга) равна: 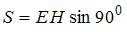. Такж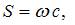е где 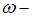объемная плотность энергии, 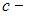скорость света. Следовательно, .

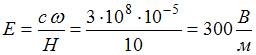4.4.7. Плоская электромагнитная волна распространяется в диэлектрике с проницаемостью ε=4. Если амплитудное значение электрического вектора волны E₀=0,55 мВ/м, то интенсивность волны равна …

(Электрическая постоянная равна ε₀=8,85∙10^-12 Ф/м. Полученный ответ умножьте на 10¹⁰ и округлите до целого числа.)

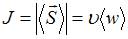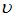Решение:Интенсивностью волны называется скалярная величина, равная модулю среднего значения вектора плотности потока энергии (вектора Умова – Пойнтинга) , где – скорость волны, 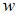– объемная плотность ее энергии. Среднее значение объемной плотности энергии электромагнитной волны определяется выражением 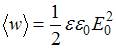, а скорость волны в сре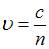де , где 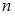– абсолютный показатель преломления среды, причем 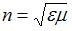. Для неферромагнитных сред 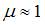. Таким образом, выражение для интенсивности электромагнитной волны можно представить в виде .

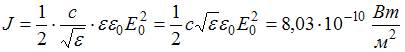4.4.8. Показатель преломления среды, в которой распространяется электромагнитная волна с напряженностями электрического и магнитного полей соответственно E=750 В/м, H=2 А/м и объемной плотностью энергии ω=10 мкДж/м³, равен …

Решение:Плотность потока энергии электромагнитной волны (вектор Умова – Пойнтинга) равна: 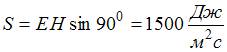. Такж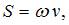е где 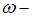объемная плотность энергии, 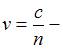скорость электромагнитной волны в среде, 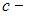скорость электромагнитной волны в вакууме, 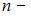показатель преломления.

Следовательно, 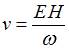и