Цифровой согласованный фильтр

Поскольку согласованный фильтр должен выдавать на выходе сигнал, совпадающий по форме с корреляционной функцией входного сигнала, то алгоритм обработки сигнала в этом случае можно построить по схеме рис.14.

Рис. 14

На вход блока дискретного преобразования Фурье подаются закодированные в цифровой код отсчеты комплексной огибающей дискретизированного радиосигнала 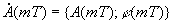. На его выходе образуется последовательность спектральных коэффициентов 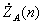, которая вместе с набором коэффициентов комплексно-сопряженных известному сигналу 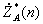поступает на набор перемножителей, осуществляющих перемножение каждого n-го числа.

На выходе блока обратного дискретного преобразования Фурье формируется последовательность отсчетов выходного сигнала, которые далее подвергаются обработке с целью выработки решения.

Достоинством цифровой согласованной фильтрации по сравнению с аналоговой является возможность реализации устройств с любыми характеристиками в пределах полосы частот, обеспечиваемой быстродействием АЦП и ЦАП. Все сводится к выбору весовых коэффициентов, при этом обеспечивается высокая точность и стабильность характеристик цифровых фильтров.

Теорема Шеннона.

Теорема Шеннона — Хартли в теории информации — применение теоремы кодирования канала с шумом к архетипичному случаю непрерывного временно́го аналогового канала коммуникаций, искажённого гауссовским шумом. Теорема устанавливает шенноновскую ёмкость канала, верхнюю границу максимального количества безошибочных цифровых данных (то есть, информации), которое может быть передано по такой связи коммуникации с указанной полосой пропускания в присутствии шумового вмешательства, согласно предположению, что мощность сигнала ограничена, и гауссовский шум характеризуется известной мощностью или мощностью спектральной плотности. Закон назван в честь Клода Шеннона и Ральфа Хартли.

Рассматривая все возможные многоуровневые и многофазные методы шифрования, теорема Шеннона — Хартли утверждает, что пропускная способность канала 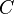, означающая теоретическую верхнюю границу скорости передачи данных, которые можно передать с данной средней мощностью сигнала 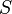через аналоговый канал связи, подверженный аддитивному белому гауссовскому шуму мощности 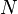равна:

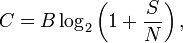
где

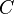— пропускная способность канала, бит/с;

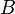— полоса пропускания канала, Гц;

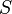— полная мощность сигнала над полосой пропускания, Вт или В²;

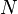— полная шумовая мощность над полосой пропускания, Вт или В²;

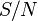— частное от деления отношения сигнала к его шуму (SNR) на гауссовский шум, выраженное как отношение мощностей.

Циклические коды.

Циклические коды являются частным случаем линейных и представляют собой наиболее разработанную часть последних. Основным их достоинством является простота технической реализации, благодаря чему они и обратили на себя внимание специалистов. Ценным свойством таких кодов является способность обнаруживать не только одиночные ошибки, но и пакеты ошибок. Пакетом ощибок длиной L называют число разрядов сообщения, искаженных подряд.
Свое название циклические коды получили из-за следующего свойства: если комбинация
a_n-1a_n-2 ... a₁a₀

относится к коду, то комбинация, полученная путем циклического сдвига элементов, т.е. комбинация
a_n-2 ... a₁a₀a_n-1,

также относится к коду. Направление сдвига не имеет значения. Один сдвиг в одном направлении эквивалентен n-1 сдвигам в другом направлении.

Математической основой построения циклических кодов является представление кодовых комбинаций в виде многочленов от некоторой переменной x с коэффициентами, равными элементам кодовых комбинаций, и операцией по mod2. Кодовая комбинация

a_n-1a_n-2 ... a₁a₀

представляется многочленом
a_n-1x^n-1 + a _n-2x^n-2 + ... + a₁x + a₀

Кодовый полином

Циклический код строится с помощью так называемого порождающего многочлена g(x) степени r. Признаком принадлежности n-разрядной комбинации данному коду является делимось соответствующего ей многочлена на порождающий. Если многочлен принятой комбинации делится на порождающий, то считается, что она совпадает с посланной. Если деление происходит с остатком, то принятая комбинация к коду не относится, т.е. произошло наложение ошибки. Вид остатка при достаточной избыточности позволяет указать место ошибки.