Атмосфера статикасы, статика теңдеулерін талдау; барометрлік формула; біртекті атмосфера үшін барометрлік теңдеу

Жер бетіне қатысты атм/а тыныштықта тұрса,атм құрылысын анықтайтын заңдылықтар бөлігін – атм/қ статикасыдеп атайды. Яғни ол горизонтальді, вертикальді бағытта қозғалмайтын болып келеді.Егер жүйеге барлық әсер ететін күштер жиынтығы 0-ге тең болса,онда осы жүйе тепе-теңдікте немесе тыныштықта байқалады. Барлық әсер ететін күштер массалық, сыртқы болып бөлінеді. Массалық күштерге: ауырлық, Кариолис күштері жатады. Ал сыртқы күштерге: қысым, үйкеліс күштері жатады. Бірақ, Кариолис күші мен үйкеліс күштері атмосфера қозғалыста ғана кезде байқалады. Сондықтан, тыныштықта тұрғанда әсер ететін күштер ауырлық, қысым күші болып табылады. Еркін түсу үдеуі гравитациялық тартылыс үдеуінің, ортадан тебу үдеуінің векторлық қосындысы болып табылады, келесідей g=ga+z;

g - еркін түсу үдеуі,

ga- гравитациялық үдеуі,

z-ортадан тебу векторлық үдеуі.

Ортадан тебу күші жердің тәуліктік айналымы нәтижесінде пайда болады. әр нүктесінде ол жердің айналу осіне перпендикуляр болады. Ауырлық күші әсер ететін бағыты нақты вертикаль деп аталады. Ал беткейінің кез келген нүктесінде ауырлық күші перпендикуляр болыпдеңгейлік беткей д/а. r арақашықтықтан жердің ортасына дейін және географиялық ендікке еркін түсу үдеуі бағыныштылығы келесі теңдеуімен сипатталады:

*(3

– элипсоидтық экваториалды радиусы

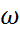- жердің тәуліктік айналымының бұрыштық жылд.

М- жер массасы

- универсалды гравитациялық тұрақтысы

Ауырлық күші: F=g

Берілген ауа бағаны вертикальды бағытта да қозғалмай тыныштықта тұрғандықтан, салмағы болса да ол бір деңгейде қалқып тұрады. Яғни жоғары бағытталған қысым мен ауырлық күші теңеп тұр:

p=F+(p+dp) => p-F-p-dp=>-F-dp=0

енді ауырлық күшін ашып жазсақ статиканың негізгі теңдеуі шығады:

-g dz=0 немесе –dp= g dz

g-еркін түсу үдеуі (м/ )

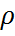-тығыздық

dz-биіктік

егер осы формуланың 2 жағын dz – ке түрлендірсек, атмосфера статикасының 2-ші түрі шығады.

- ауа қысымының вертикальды градиенті

Атмосфера статиканың негізгі теңдеуінен 3 маңызды қорытынды алуға болады:

1. Жер бетінен биіктеген сайын,атмосфера қысымы әрқашан азаяды.

2. Статиканың негізгі теңдеуін интегралдап, белгілі деңгейдегі қысымын сипаттайтын теңдеуді аламыз:

z-берілген деңгейдегі биіктік

-атм-ң жоғарғы шекарасының биіктігі

Бұл теңдеу атмосфера қысымының берілген деңгейден атмосфера жоғарғы шекарасына дейінгі бірлік ауданды ауа бағанның салмағына тең екенін көрсетеді.

3. Биіктік б/а қысымның азаю жылдамдығы туралы қорытынды: статиканың негізгі теңдеуі б/а бірлік биіктікке көтерілгенде қысымның азаюы үлкен болады, тығыздық пен еркін түсу үдеуі үлкен болады. Осы теңдеуде тығыздық атқаратын рөл маңызды және ол биіктеген сайын азаяды. Яғни жер бетінен биіктеген сайын қысымның вертик градиенті азаяды.

Статиканың негізгі теңдеуі қозғалыссыз тыныштықтағы атмосфера қысымының биіктік бойынша өзгеруін сипаттайды.

Барометрлік теңдеулер (Лаплас, Баббине).Статиканың негізгі теңдеуінен қысымның, тығыздықтың ж/е ауа салмағының вертикаль б/ша өзгерісінің заңдылықтары анықталады. Бірақ дифференциалды түрде статиканың негізгі теңдеуін тек тығыздығы тұрақты ауаның жіңішке қабатына ғана қолдануға болады. Тәжірибе жүйесінде темп/мен тығыздықтың биіктік б/ша әртүрлі өзгеру жағдайында қысымның биіктік б/ша таралуын білу керек. Осы мақсатта статиканың негізгі теңдеуі интегралды түрде қолдануға болады. Оларды Барометр теңдеуі д.а. Статиканың негізгі теңдеуін интегралды түрде жазамыз:

немесе

Яғни,

-жер бетіндегі қысым

биіктігіндегі қысым