Термодинамические циклы двигателей

ВНУТРЕННЕГО СГОРАНИЯ И ГАЗОТУРБИННЫХ УСТАНОВОК

Термодинамические циклы ДВС со смешанным процессом подвода теплоты

Двигатели внутреннего сгорания (ДВС) со смешанным подводом теплоты являются главными двигателями морских транспортных судов с судовой дизельной установкой (СДУ). Для исследования эффективности термодинамических циклов таких ДВС решим ряд задач.

Задача 1

Для цикла ДВС со смешанным подводом теплоты заданы следующие начальные параметры рабочего тела: р₁ = 0,095 МПа, t₁ = 40 °С и характеристики цикла: степень сжатия ε = 14; степень повышения давления λ = 1,35; степень предварительного расширения ρ = 1,6.

Изобразить цикл на рабочей и тепловой диаграммах. Определить параметры рабочего тела в характерных точках цикла, работу расширения, сжатия и суммарную (полезную), количество подводимой, отводимой и превращаемой в работу теплоты, а также термический КПД цикла.

Решение

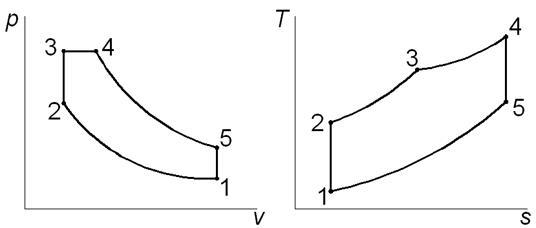
Рис. 2.1. Термодинамический цикл ДВС со смешанным подводом теплоты

на рабочей и тепловой диаграммах:

1-2 – адиабатное сжатие; 2-3 – изохорный подвод теплоты;

3-4 – изобарный подвод теплоты; 4-5 – адиабатное расширение;

5-1 – изохорный отвод теплоты

При расчете и анализе термодинамических циклов ДВС полагают, что их рабочим телом является идеальный газ со свойствами воздуха. Поскольку воздух является смесью двухатомных газов азота и кислорода, его теплоёмкости c_v и c_p и показатель адиабаты k равны

;

;

.

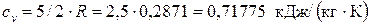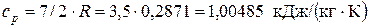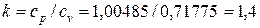В точке 1 определяем значение удельного объема из уравнения состояния идеального газа

.

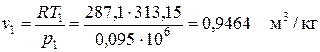Точка 2

Рассчитываем значение v₂ из определения понятия степени сжатия

.

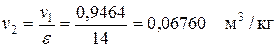Температуру рассчитываем по уравнению изоэнтропы

.

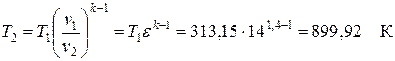Давление определяем из уравнения состояния идеального газа

.

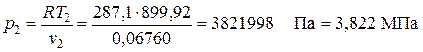Точка3

При изохорном подводе теплоты значение удельного объема v₃= v₂ = 0,0676 м³/кг. Давление и температуру определяем, зная определение и значение степени повышения давления λ

р₃ = р₂·λ = 3,822·1,45 = 5,160 МПа,

Т₃ = Т₂λ = 899,92·1,35 = 1214,89 К.

Точка4

При изобарном подводе теплоты значение давления р₄ = р₃ = = 5,160 МПа. Удельный объем и температуру рассчитываем, используя значение степени предварительного расширения ρ

v₄ = v₃ρ = 0,06760·1,6 = 0,1082 м³/кг

Т₄ = Т₃ρ = 1214,89·1,6 = 1943,82 К.

Точка5

Значение удельного объема в конце адиабатного процесса расширения 4-5 определяем из теории построения термодинамического цикла ДВС v₅ = v₁= = 0,9464 м³/кг. Температуру рассчитываем из уравнения изоэнтропы

.

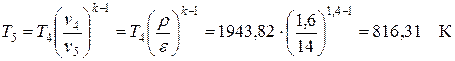Давление находим из уравнения состояния идеального газа

.

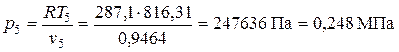Результаты расчетов записываем в таблицу:

Точки	р, МПа	v, м3/кг	Т, К
	0,095	0,9464	313,15
	3,822	0,0676	899,92
	5,160	0,0676	1214,89
	5,160	0,1082	1943,83
	0,248	0,9464	816,31

На основании рассчитанных значений параметров рабочего тела ДВС (идеального газа со свойствами воздуха) определяем энергетические эффекты (работу и теплоту) во всех процессах, образующих термодинамический цикл.

Работа:

— в изоэнтропном процессе сжатия 1-2

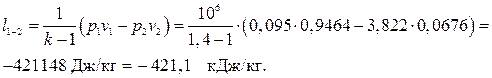
— в изобарном процессе расширения 3-4

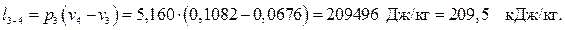
— в изоэнтропном процессе расширения 4-5

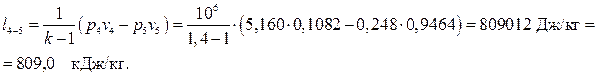
Суммарная (полезная) работа в цикле

.

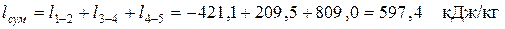Количества теплоты, подводимые в изохорном процессе 2-3 и в изобарном 3-4, соответственно равны:

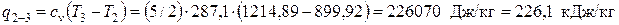
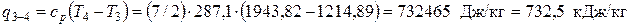
Количество теплоты, отводимой в процессе 5-1

.

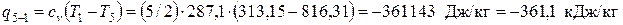Полезно используемая теплота (превращаемая в работу)

.

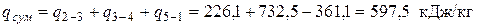Результаты расчетов записываем в таблицу:

Процесс	l, кДж/кг	q, кДж/кг
1-2 (адиабатное сжатие)	-421,1
2-3 (изохорный подвод теплоты)		226,1
3-4 (изобарный подвод теплоты)	209,5	732,5
4-5 (адиабатное расширение)	809,0
5-1 (изохорный отвод теплоты)		-361,1
Сумма	597,4	597,5

Рассчитанные суммарные значения q и l согласуются в пределах 0,02 %. Это свидетельствует о высокой точности выполненных расчетов.

Термический КПД цикла

.

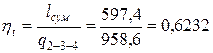Для проверки рассчитываем значение термического КПД по заданным характеристикам цикла

.

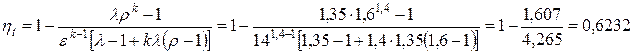Полученные значения η_t совпали, что также подтверждает высокую точность всех рассчитанных величин.

Задача 2

В цикле поршневого двигателя со смешанным подводом теплоты начальное давление р₁ = 0,09 МПа, начальная температура t₁ = 50 °С, степень сжатия ε = 15, максимальное давление – 5,4 МПа, количество подводимой теплоты q₁ = 900 кДж/кг, рабочее тело – идеальный газ со свойствами воздуха.

Какая часть теплоты подводится в изохорном процессе и каково значение термического КПД цикла?

Решение

Для ответа на первый вопрос необходимо определить значения температуры в начале и в конце изохорного процесса 2-3 (Т₂ и Т₃). Значение Т₂ рассчитываем из уравнения изоэнтропы 1-2

.

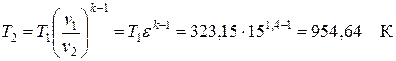Для расчета значения Т₃ необходимо знать степень повышения давления λ = р₃/р₂. Поэтому определяем р₂ из уравнения адиабаты 1-2

.

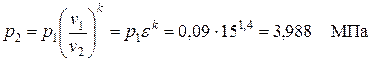Поскольку в рассматриваемом цикле р₃ = р_макс = 5,4 МПа, значение λ равно

λ = р₃/р₂ = 5,4/3,988 = 1,354.

Температура в конце изохорного подвода теплоты

Т₃ = Т₂λ = 954,65·1,354 = 1292,60 К.

Количество теплоты, подводимой в изохорном процессе

,

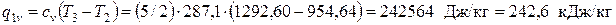что составляет 27,0 % от всей подводимой в цикле теплоты.

Для расчета значения термического КПД цикла необходимо определить количество отводимой теплоты, то есть температуру в точке 5, либо определить третью характеристику цикла − степень предварительного расширения ρ.

Значение ρ можно найти, рассчитав предварительно температуру Т₄ из уравнения для расчета количества теплоты, подводимой в изобарном процессе

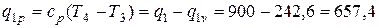. кДж/кг,

тогда

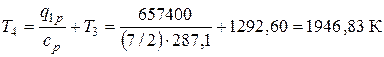
Степень предварительного расширения равна

ρ = Т₄/Т₃ = 1946,83/1292,60 = 1,506.

Зная характеристики цикла, определяем значение термического КПД

.

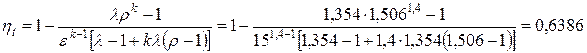Для проверки определяем температуру Т₅ и количество отводимой в цикле теплоты

.

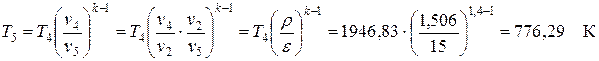
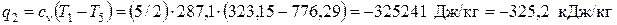На основании величин q₁ и q₂ рассчитываем значение термического КПД

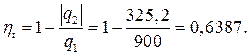
Значения η_t, рассчитанные двумя способами, согласуются в пределах 0,02 %, что свидетельствует о высокой точности выполненных расчетов.

Задача 3

Рассчитать параметры рабочего тела во всех характерных точках идеализированного обратимого термодинамического цикла ДВС со смешанным процессом подвода теплоты. Сделать заключение об его эффективности, если известны следующие данные: температура воздуха в начале процесса сжатия t₁= 24 °С; удельный объем газов в точке 5 v₅= 0,47071 м³/кг; теплота, подводимая в цикле q₁= 722,64 кДж/кг; работа адиабатного сжатия воздуха l_1-2= – 501,85 кДж/кг; изменение энтропии в изохорном процессе подвода теплоты 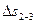= 0,35943 кДж/(кг·К).

Решение

Параметры рабочего тела в точке1:

– удельный объем

,

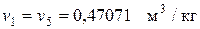исходя из теории построения теоретического цикла ДВС;

– давление из уравнения состояния идеаьного газа

.

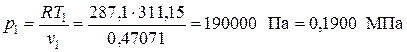Параметры рабочего тела в точке 2:

– температуру определяем из соотношения между работой адиабатного процесса сжатия и изменением внутренней энергии рабочего тела

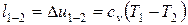; тогда ;

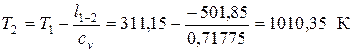– удельный объем и давление определяем из уравнения адиабаты 1-2

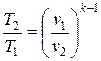, тогда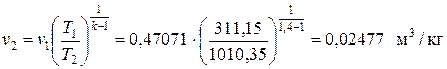

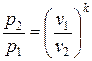, от сюда .

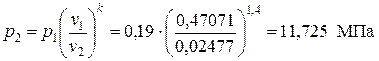Параметры рабочего тела вточке3.

Процесс 2-3 – изохорный, поэтому .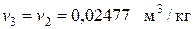

В условии задачи задано изменение энтропии в процессе 2-3

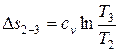, тогда .

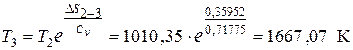Как известно, в изохорном процессе температура и давление изменяются прямо пропорционально

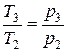, отсюда .

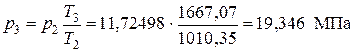Проверка.

Из уравнения состояния идеального газа

.

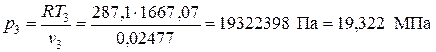Значения р₃ рассчитанные по двум независимым соотношениям согласуются вполне удовлетворительно (с погрешностью 0,12 %).

Параметры рабочего тела в точке 4.

Процесс 3-4 – изобарный, поэтому .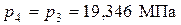

В условии задачи задано общее количество теплоты q₁, подводимой в цикле

.

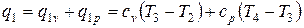Следовательно, количество теплоты, подводимое в процессе 3-4,равно

.

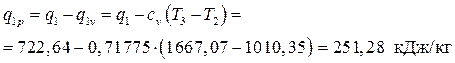С другой стороны

,

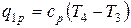тогда .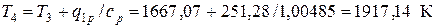

В изобарном процессе температура и удельный объем изменяются прямо пропорционально

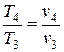, тогда .

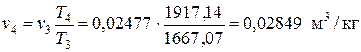Проверка.

Из уравнения состояния идеального газа

.

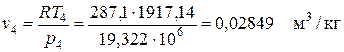Значения v₄, рассчитанные по двум независимым соотношениям, совпали.

Параметры рабочего тела в точке 5.

Процесс4-5– адиабатный, тогда:

– температура

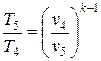, отсюда ;

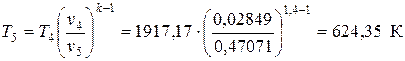– давление

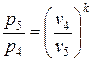, отсюда .

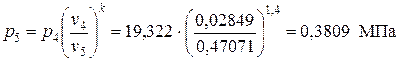Результаты расчетов записываем в таблицу:

Точки	р, МПа	v, м3/кг	Т, К
	0,1900	0,47071	311,15
	11,725	0,02477	1010,35
	19,322	0,02477	1667,07
	19,322	0,02849	1917,14
	0,3809	0,47071	624,35

Первая комплексная проверка точности выполненных расчетов термических параметров состояния рабочего тела ДВС в характерных точках цикла состоит в сопоставлении суммарной работы цикла, рассчитанной через p и v, c суммарной теплотой, рассчитанной через T, с_p и с_v. Вторая проверка точности расчетов состоит в сопоставлении значений термического КПД, рассчитанных из различных соотношений, включающих как термические, так и калорические параметры состояния.

Первоначально рассчитываем значения деформационной работы:

– в адиабатном процессе сжатия 1-2

;

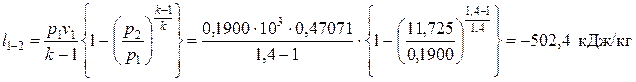– в изохорном процессе 2-3 – ;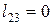

– в изобарном процессе предварительного расширения 3-4

;

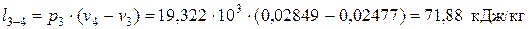– в адиабатном процессе последующего расширения 4-5

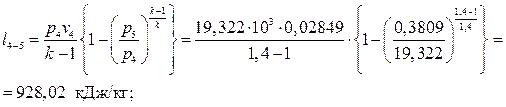
– в изохорном процессе 5-1 – .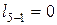

Теперь рассчитываем значения теплоты:

– в адиабатном процессе сжатия 1-2 – ;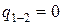

– в изохорном процессе 2-3

;

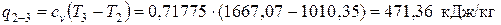– в изобарном процессе расширения 3-4

;

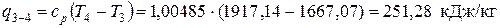– в адиабатном процессе расширения 4-5 – ;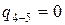

– в изохорном процессе 5-1

.

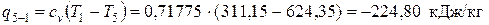Результаты расчетов записываем в таблицу:

Процесс	l, кДж/кг	q, кДж/кг
1-2 адиабатное сжатие	-502,4
2-3 изохорный подвод теплоты		471,36
3-4 изобарный подвод теплоты	71,88	251,28
4-5 адиабатное расширение	928,02
5-1 изохорный отвод теплоты		-224,80
Сумма	497,50	497,84

Анализируя данные таблицы можно сделать вывод о хорошей точности выполненных расчётов, так как суммарная теплота мало отличается от суммарной работы: всего лишь на 0,34 кДж/кг, или на 0,07 %.

Теперь проверяем точность выполненных расчетов, сопоставляя значения термического КПД, рассчитываемые из следующих соотношений:

— из соотношения полезной работы цикла и подводимой в цикле теплоты

,

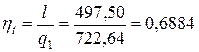где l – суммарная работа цикла (см. предыдущую таблицу);

— из соотношения подводимой и отводимой в цикле теплоты

,

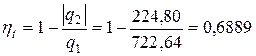где q₁ и q₂ – значения подводимой и отводимой в цикле теплоты:

– подводимая теплота

,

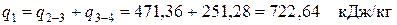– отводимая теплота

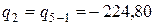кДж/кг;

— из соотношения через характеристики цикла ДВС

,

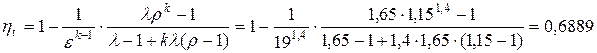где 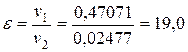– степень сжатия;

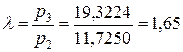– степень повышения давления;

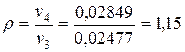– степень предварительного расширения.

Термический КПД эквивалентного цикла Карно

,

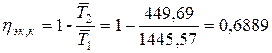где 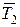– средняя температура отвода теплоты

,

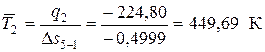Δs_5-1 – изменение энтропии в изохорном процессе отвода теплоты 5-1

,

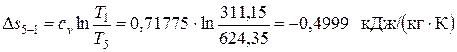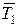– средняя температура подвода теплоты

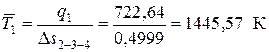
Δs_2-3-4 – изменение энтропии в процессе 2-3-4

.

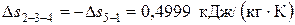Таким образом, значения КПД, рассчитанные из 4-х независимых соотношений, хорошо согласуются. Небольшое расхождение (0,07 %) между значениями КПД, рассчитанными через работу цикла l и через значения теплот q₁ и q₂, объясняется отмеченным выше расхождением между суммарными значениями работы и теплоты в цикле.

Термический КПД предельного цикла Карно

,

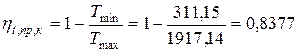где Т_min, и T_max– минимальное и максимальное значения температуры в рассматриваемом цикле.

Степень совершенства исследуемого цикла ДВС

.

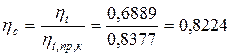Следовательно, эффективность данного цикла ДВС ниже, чем предельного цикла Карно почти на 18 %.

Задача 4. Какую дополнительную работу можно получить, расширив отработавшие газы ДВС, рассмотренного в предыдущей задаче, до атмосферного давления в газовой турбине комбинированного двигателя?

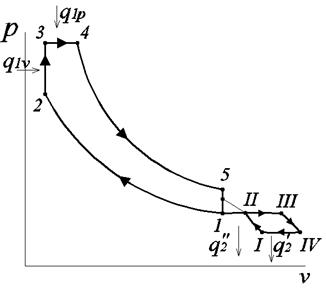
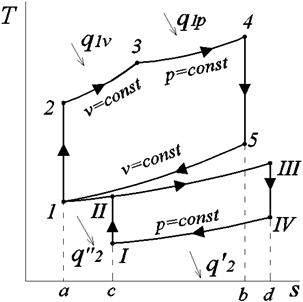
Рис. 2.2. Термодинамический цикл комбинированного двигателя

на рабочей и тепловой диаграммах:

обозначения в цикле газотурбинного двигателя: I-II – изоэнтропное сжатие

воздухав компрессоре; II-I – изобарный отвод теплоты от наддувочного воздуха; II-III – изобарный подвод теплоты к газу перед турбиной; III-IV – изоэнтропное расширение в турбине;IV-I – изобарный отвод теплоты в окружающую среду в цикле газотурбинного двигателя;

обозначения в цикле ДВС:1-2 – изоэнтропное сжатиевоздуха в цилиндре дизеля; 2-3 и 3-4 – изохорный и изобарный подвод теплоты к рабочему телу в цилиндре; 4-5 – изоэнтропное расширение в цилиндре; 5-1 – изохорный отвод теплоты от отработавшего газа ДВС

Решение

Комбинированный двигатель состоит из поршневого ДВС и открытой газотурбинной установки (ГТУ), которая используется как для наддува ДВС, так и для производства полезной работы. Термодинамический цикл комбинированного двигателя приведен на рис. 2.2.

В предыдущей задаче 3 начальное давление воздуха в цикле ДВС равно 0,19 МПа и обеспечивается предварительным сжатием подаваемого в цилиндр дизеля воздуха, сжимаемого в компрессоре, обычно работающего на отработавших газах ДВС.

Как известно, в открытой ГТУ теплота к рабочему телу подводится по изобаре (см. рис. 2.2). Тогда

,

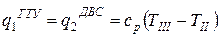где T_II — температура воздуха после компрессора, которая определяется из уравнения адиабатного процесса I-II

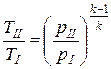, тогда .

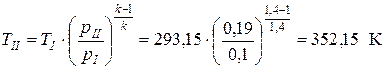При расчете Т_II приняты значения давления 0,1 МПа и температуры ат-мосферного воздуха 20 °С.

Из уравнения для расчета подводимой теплоты в изобарном процессе определяем температуру рабочего тела перед турбиной

.

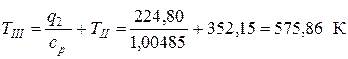где 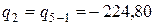кДж/кг – теплота отводимая в цикле ДВС.

Определяем удельный объем в точках I, II и III из уравнения состояния идеального газа

точка I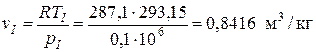

точка II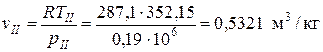

точка III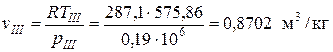

Температура в конце адиабатного расширения газов в турбине (точка IV)

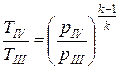, тогда .

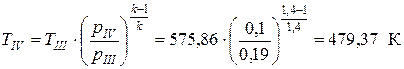Удельный объем газов в конце процесса расширения газов в турбине

.

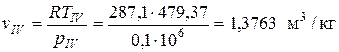Теплота, отводимая в цикле ГТУ I-II-III-IV-I

.

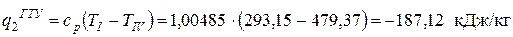Количество теплоты, превращаемой в работу в цикле ГТУ

.

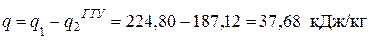Рассчитаем теперь работу цикла ГТУ путем непосредственного расчета значений работы отдельных процессов через переменные p и v.

Техническая работа:

— получаемая при адиабатном расширении газов в турбине (процесс III-IV)

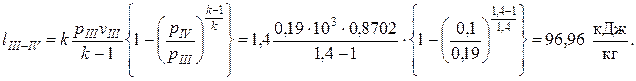
— затрачиваемая на адиабатное сжатие воздуха в компрессоре (процесс I-II)

.

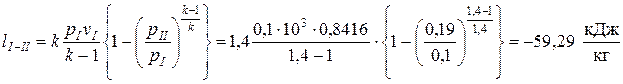— изобарных процессов подвода II-III и отвода теплоты IV-I равны нулю.

Суммарная (полезная) работа, получаемая в цикле ГТУ равна

.

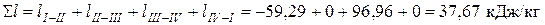Значения работы, рассчитанные двумя способами, практически совпали.

Итак, используя энергию отработавших газов ДВС в комбинированном двигателе, можно дополнительно получать полезную работу помимо работы, используемой для сжатия наддувочного воздуха. В данной задаче такая работа равна 37,67 кДж/кг. Дополнительную работу можно использовать, например, для привода насосов охлаждающей воды главного двигателя судовой дизельной установки. Это повысит эффективность судовой энергетической установки (но несколько усложнит её).