Взаимная индукция
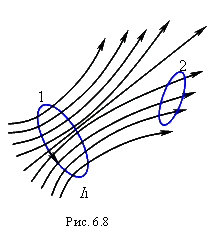 |
Рассмотрим два неподвижных контура 1 и 2, расположенных достаточно близко друг к другу (рис. 6.8). Будем полагать, что среда является неферромагнитной. Если в контуре 1 течет ток силой, то он создает через контур 2 магнитный поток, пропорциональный 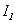 :
:
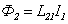 . . | (6.6) |
Аналогично, если в контуре 2 течет ток силой 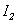 , он создает магнитный поток
, он создает магнитный поток 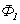 через контур 1:
через контур 1:
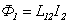 . . | (6.7) |
Коэффициенты пропорциональности 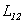 и
и 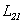 называют взаимной индуктивностью контуров. Из (6.6) и (6.7) видно, что взаимная индуктивность численно равна магнитному потоку через один из контуров при единичном токе в другом контуре. Коэффициенты
называют взаимной индуктивностью контуров. Из (6.6) и (6.7) видно, что взаимная индуктивность численно равна магнитному потоку через один из контуров при единичном токе в другом контуре. Коэффициенты 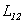 и
и 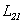 зависят от формы, размеров, взаимного расположения контуров, а также от магнитных свойств среды, окружающей контуры.
зависят от формы, размеров, взаимного расположения контуров, а также от магнитных свойств среды, окружающей контуры.
Можно показать, что при отсутствии ферромагнетиков коэффициенты 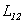 и
и 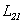 одинаковы:
одинаковы: 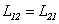 . Это свойство называется теоремой взаимности. Теорема взаимности позволяет не делать различия между
. Это свойство называется теоремой взаимности. Теорема взаимности позволяет не делать различия между 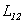 и
и 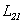 , а говорить просто о взаимной индуктивности двух контуров. Согласно теореме взаимности, если в контурах текут одинаковые токи, то магнитный поток через контур 1, созданный током в контуре 2, равен магнитному потоку через контур 2, созданному током в контуре 1.
, а говорить просто о взаимной индуктивности двух контуров. Согласно теореме взаимности, если в контурах текут одинаковые токи, то магнитный поток через контур 1, созданный током в контуре 2, равен магнитному потоку через контур 2, созданному током в контуре 1.
Если контуры неподвижны и ферромагнетиков вблизи них нет, то при изменении силы тока в одном из контуров в другом контуре возникает электродвижущая сила индукции. Это явление называется явлением взаимной индукции. Согласно закону электромагнитной индукции электродвижущие силы индукции, возникающие в контурах 1 и 2, равны соответственно
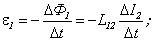
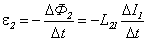 .
.
Если в каком-либо контуре, например, в контуре 1 есть внешний источник электродвижущей силы 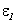 , то с учетом явления самоиндукции полную электродвижущую силу, действующую в этом контуре, можно записать следующим образом:
, то с учетом явления самоиндукции полную электродвижущую силу, действующую в этом контуре, можно записать следующим образом:
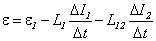 ,
,
где 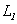 – индуктивность контура 1. Если сопротивление контура 1 равно
– индуктивность контура 1. Если сопротивление контура 1 равно 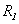 , то, согласно закону Ома, сила тока в этом контуре будет равна
, то, согласно закону Ома, сила тока в этом контуре будет равна
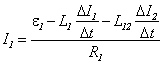 .
.
Аналогичное соотношение можно записать и для определения силы тока во втором контуре.
В отличие от индуктивности, которая всегда положительная, взаимная индуктивность величина алгебраическая (в частности, равная нулю). Из рис. 6.8 видно, что знак магнитного потока 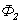 при данном направлении тока
при данном направлении тока 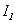 будет зависеть от выбора положительной нормали к поверхности, ограниченной контуром 2. Положительные направления для токов (и электродвижущих сил) в обоих контурах можно выбрать произвольно. При заданном направлении тока направление положительной нормали к поверхности контура определяется правилом правого винта. Если эти направления выбраны, величину
будет зависеть от выбора положительной нормали к поверхности, ограниченной контуром 2. Положительные направления для токов (и электродвижущих сил) в обоих контурах можно выбрать произвольно. При заданном направлении тока направление положительной нормали к поверхности контура определяется правилом правого винта. Если эти направления выбраны, величину 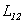 нужно считать положительной, когда при положительных токах магнитные потоки взаимной индукции через контуры оказываются также положительными, то есть совпадают по знаку с потоками самоиндукции.
нужно считать положительной, когда при положительных токах магнитные потоки взаимной индукции через контуры оказываются также положительными, то есть совпадают по знаку с потоками самоиндукции.
Другими словами, 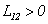 , если при положительных токах в обоих контурах они «подмагничивают» друг друга, в противном случае
, если при положительных токах в обоих контурах они «подмагничивают» друг друга, в противном случае 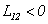 . В частных случаях можно заранее так установить положительные направления обхода контуров, чтобы получить желательный нам знак величины
. В частных случаях можно заранее так установить положительные направления обхода контуров, чтобы получить желательный нам знак величины 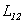 .
.
Пример
 |
При отсутствии устойчивого сигнала сотовой связи телефон становится более чувствительным к электромагнитным помехам. Происходит это из-за изменения сигнала вследствие явления взаимоиндукции. Пример такого эффекта – ухудшение приема телефона при приближении к телевизору или радиоприемнику.
6.6. Примеры на применение явления
электромагнитной индукции
