КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ. Определить ЭДС Холла и концентрацию носителей тока в полупроводнике методом, использующим эффект Холла
ЛАБОРАТОРНАЯ РАБОТА
№ 2.9
ИССЛЕДОВАНИЕ
ЭФФЕКТА ХОЛЛА
МЕТОДИЧЕСКОЕ ПОСОБИЕ
Минск 2010
ЛАБОРАТОРНАЯ РАБОТА № 2.9
ИССЛЕДОВАНИЕ ЭФФЕКТА ХОЛЛА
ЦЕЛЬ РАБОТЫ
Определить ЭДС Холла и концентрацию носителей тока в полупроводнике методом, использующим эффект Холла.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
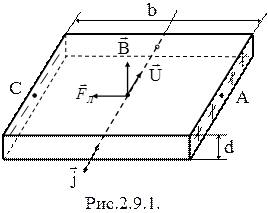
В 1880г. Холлом было обнаружено явление, названное впоследствии гальваномагнитным эффектом Холла. Сущность эффекта Холла состоит в следующем. Если пластинку проводника или полупроводника, по которому идет постоянный электрический ток плотностью 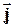 , поместить в однородное магнитное поле
, поместить в однородное магнитное поле 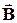 перпендикулярное направлению движения носителей тока (рис. 2.9.1), то между двумя точками противоположных граней пластинки (например, A и C), расположенными на прямой, перпендикулярной как направлению плотности тока
перпендикулярное направлению движения носителей тока (рис. 2.9.1), то между двумя точками противоположных граней пластинки (например, A и C), расположенными на прямой, перпендикулярной как направлению плотности тока 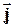 , так и вектору магнитной индукции
, так и вектору магнитной индукции 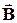 , возникает разность потенциалов
, возникает разность потенциалов 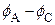 , называемая ЭДС Холла (
, называемая ЭДС Холла ( 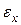 ). Величина этой ЭДС при условии малой толщины d пластинки
). Величина этой ЭДС при условии малой толщины d пластинки
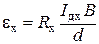 , где Iдх= j S = j b d
, где Iдх= j S = j b d
или
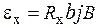
 (2.9.1)
(2.9.1)
где Rx- постоянная Холла;
b – ширина пластинки.
.
Эффект Холла объясняется действием магнитного поля на движущиеся электрические заряды. В отсутствие магнитного поля ток в пластинке обусловлен электрическим полем 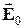 . Эквипотенциальные поверхности этого поля образуют систему перпендикулярных вектору
. Эквипотенциальные поверхности этого поля образуют систему перпендикулярных вектору 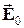 плоскостей. Две из них изображены на рис.2.9.2 сплошными линиями. Носители тока - электроны - имеют отрицательный заряд, поэтому скорость их упорядоченного движения
плоскостей. Две из них изображены на рис.2.9.2 сплошными линиями. Носители тока - электроны - имеют отрицательный заряд, поэтому скорость их упорядоченного движения 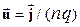 , (n – концентрация носителей заряда , заряд электрона q = –1,6·10-19 Кл) направлена противоположно вектору плотности тока
, (n – концентрация носителей заряда , заряд электрона q = –1,6·10-19 Кл) направлена противоположно вектору плотности тока 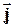 . В магнитном поле на носители тока действует сила
. В магнитном поле на носители тока действует сила 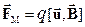 перпендикулярная средней скорости упорядоченного движения носителей тока
перпендикулярная средней скорости упорядоченного движения носителей тока 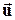 и индукции магнитного поля
и индукции магнитного поля 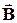 . Под действием этой силы носители тока отклоняются к одной из граней пластинки и накапливаются там, создавая отрицательный заряд. На противоположной грани будет оставаться нескомпенсированный положительный заряд. В результате возникает электрическое поле
. Под действием этой силы носители тока отклоняются к одной из граней пластинки и накапливаются там, создавая отрицательный заряд. На противоположной грани будет оставаться нескомпенсированный положительный заряд. В результате возникает электрическое поле 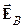 , поперечное по отношению к
, поперечное по отношению к 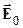 и
и 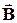 (рис. 2.9.2).
(рис. 2.9.2).
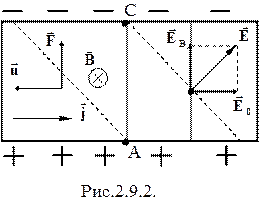 Сила
Сила 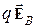 , действующая со стороны поперечного электрического поля на заряд q направлена в сторону, противоположную направлению магнитной силы
, действующая со стороны поперечного электрического поля на заряд q направлена в сторону, противоположную направлению магнитной силы 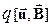 . В случае равновесного процесса прохождения тока по пластинке эти силы взаимно уравновешиваются, т.е.
. В случае равновесного процесса прохождения тока по пластинке эти силы взаимно уравновешиваются, т.е.
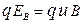 (2.9.2)
(2.9.2)
Поля 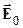 и
и 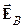 складываясь, дают результирующее поле
складываясь, дают результирующее поле 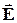 . Эквипотенциальные поверхности, перпендикулярные вектору напряженности поля
. Эквипотенциальные поверхности, перпендикулярные вектору напряженности поля 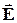 , изображены на рис. 2.9.2 пунктиром. Точки A и С, лежавшие на одной эквипотенциальной поверхности, теперь принадлежат разным эквипотенциальным поверхностям и имеют разные потенциалы. Учитывая, что
, изображены на рис. 2.9.2 пунктиром. Точки A и С, лежавшие на одной эквипотенциальной поверхности, теперь принадлежат разным эквипотенциальным поверхностям и имеют разные потенциалы. Учитывая, что 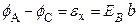 , а
, а 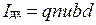 возникшая между ними разность потенциалов
возникшая между ними разность потенциалов
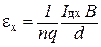 (2.9.3)
(2.9.3)
Коэффициент 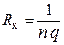 является основной количественной характеристикой эффекта Холла. Знак Rx совпадает со знаком носителей заряда. Следует отметить, что полученные результаты верны лишь приблизительно. В вышеизложенном материале предполагалось, что все носители тока движутся с одинаковой по величине скоростью, равной средней скорости упорядоченного движения. В действительности же у различных носителей тока скорости их движения неодинаковы. С учетом распределения носителей тока по скоростям, выражение для постоянной Холла приобретает вид:
является основной количественной характеристикой эффекта Холла. Знак Rx совпадает со знаком носителей заряда. Следует отметить, что полученные результаты верны лишь приблизительно. В вышеизложенном материале предполагалось, что все носители тока движутся с одинаковой по величине скоростью, равной средней скорости упорядоченного движения. В действительности же у различных носителей тока скорости их движения неодинаковы. С учетом распределения носителей тока по скоростям, выражение для постоянной Холла приобретает вид:
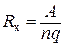 (2.9.4)
(2.9.4)
где 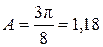
Важной характеристикой вещества является подвижность носителей тока. Подвижность носителей тока uo определяется средней скоростью, приобретенной носителями при напряженности электрического поля, равной единице, т.е.
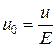 (2.9.5)
(2.9.5)
Записав закон Ома в дифференциальной форме 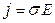 и учитывая, что j = n q u, можно определить подвижность, как
и учитывая, что j = n q u, можно определить подвижность, как
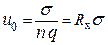 (2.9.6)
(2.9.6)
где 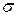 - удельная электропроводность вещества.
- удельная электропроводность вещества.
Эффект Холла является одним из наиболее эффективных методов изучения электрических свойств металлов и полупроводников. Он используется для умножения постоянных токов в аналоговых вычислительных машинах, при измерении индукции постоянных и переменных магнитных полей, преобразовании постоянного тока в переменный, измерении мощности электромагнитных полей на сверхвысоких частотах и в других областях техники.
В данной работе используется метод измерения ЭДС Холла в постоянных электрическом и магнитном полях.
Функциональная схема установки приведена на рис. 2.9.3.
 | ||||||||||||||
 | ||||||||||||||
 | ||||||||||||||
 | ||||||||||||||
 | ||||||||||||||
 | ||||||||||||||
 | ||||||||||||||
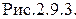 |
К полупроводниковому образцу или датчику Холла (ДХ) через электроды 1 и 2 подводится ток, электроды А и С являются зондами для измерений ЭДС Холла.
Держатель с полупроводниковым образцом устанавливается между полюсными наконечниками электромагнита (ЭМ), подключенного к источнику постоянного тока.
Величина тока, идущего через образец, регулируется потенциометром R1 и измеряется миллиамперметром (mA).
Изменение величины индукции магнитного поля в воздушном зазоре между полюсными наконечниками электромагнита осуществляется реостатом R2, а измерение значения тока Iэм производится амперметром (mА). Индукция магнитного поля определяется из выражения
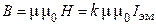 (2.9.7)
(2.9.7)
где m - относительная магнитная проницаемость сердечника электромагнита; k - коэффициент, учитывающий конструктивные особенности электромагнита.
ЭДС Холла вычисляется по формуле
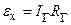 (2.9.8)
(2.9.8)
где IГ - ток, идущий через гальванометр (Г), RГ - внутреннее сопротивление гальванометра.
Если бы холловские электроды на образце были расположены строго симметрично, то при прохождении тока через образец и при отсутствии магнитного поля между электродами не обнаруживалось бы никакой разности потенциалов. Однако расположить их строго симметрично невозможно и между холловскими электродами возникает разность потенциалов UR. Потенциометром R3 выравниваются потенциалы на концах гальванометра, который при отсутствии магнитного поля должен показывать нуль. При включении магнитного поля возникает ЭДС Холла, и гальванометр показывает наличие тока. Чтобы убедиться в том, что гальванометр действительно регистрирует ток, обусловленный ЭДС Холла, следует плавно уменьшить индукцию магнитного поля, затем переключателем П1 изменить его направление на противоположное и вновь плавно увеличить индукцию магнитного поля. Стрелка гальванометра при этом должна отклониться в противоположную сторону.
Между холловскими электродами, кроме напряжения UR и ЭДС Холла, возникают и другие ЭДС, обусловленные гальваномагнитными и термомагнитными эффектами.
При определении величины ЭДС Холла для исключения напряжений, обусловленных побочными эффектами, измерения тока IГ необходимо проводить два раза при противоположных направлениях магнитного поля, а затем усреднять полученные значения:
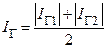 (2.9.9)
(2.9.9)
По найденным значениям IГ и по величинам тока через образец Iдх и через электромагнит Iэм определяется постоянная Холла
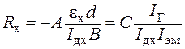 (2.9.10)
(2.9.10)
где 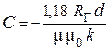 - калибровочный коэффициент.
- калибровочный коэффициент.
Значения m, k, d и допустимые значения величин Iдх и Iэм указаны на рабочем месте (m0 = 1,26×10-6 Гн/м).
ЗАДАНИЕ
1. Исследовать зависимость ЭДС Холла от индукции магнитного поля ex = f (B) при постоянном значении тока, протекающего через образец Iдх = const.
2. Результаты измерений и расчетов занести в табл. 2.9.1.
Таблица 2.9.1.
| № | Iэм, мА | В, Тл | Iдх = 4 мА | |||
| IГ1,мкА | IГ2, мкА | IГ, мкА | ex, В | |||
3. Построить зависимость ЭДС Холла от величины индукции магнитного поля eх = f (В) при Iдх = const.
4. Исследовать зависимость ЭДС Холла от величины силы тока, протекающего через образец eх = f (Iдх), при постоянном значении индукции магнитного поля B = const (Iэм = const).
5. Результаты измерений и расчетов занести в табл. 2.9.2.
Таблица 2.9.2.
| № | Iдх, мА | Iэм = 200 мА | |||
| IГ1, мкА | IГ2, мкА | IГ, мкА | ex, В | ||
| 1. | |||||
| 2. | |||||
| 3. | |||||
| 4. | |||||
| 5. |
6. Построить зависимость ЭДС Холла от силы тока, протекающего через образец eх = f (Iдх) при В = const.
7. Вычислить постоянную Холла и концентрацию носителей тока по формулам (2.9.10) и (2.9.4).
8*. Проанализировать полученные результаты на основании данных, приведенных в табл. 2.9.3. Можно ли на основании полученных данных рассчитать подвижность носителей заряда в образце?
Таблица 2.9.3
| Материалы | Rx, м3 Кл-1 | n, м-3 | s, Ом-1 м-1 | u0, м2 В-1 с-1 |
| Si Ge InSb InAs Bi | -102 -10-1 -5·10-4 -10-2 -5·10-8 | 1022 1020 1022 1021 1026 | 1,6·10-3 2,7 1,4·104 4,0·102 8,6·105 | 0,16 0,30 7,00 4,00 0,42 |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Написать и проанализировать выражение для электромагнитной силы, действующей на движущийся заряд q.
2. В чем заключается сущность эффекта Холла?
3. Как объяснить возникновение холловской разности потенциалов с точки зрения электронной теории? Вывести формулу для ЭДС Холла.
4. Дать определение подвижности носителей тока. Вывести формулу для определения подвижности носителей тока.
5. Почему измерения разности потенциалов между холловскими электродами необходимо проводить два раза при противоположных направлениях магнитного поля?
6. Можно ли в полупроводнике, обладающем только собственной проводимостью, наблюдать эффект Холла?
Литература
1. Иродов И.Е. Основные законы электромагнетизма. –М.: Высшая школа. 1983. с. 226-228.
2. Калашников С.Г. Электричество. –М.: Наука. 1977. Т.3. с. 438-443.
Приложение.
Согласно электронной теории, даже при очень больших плотностях тока средняя скорость упорядоченного движения зарядов <u> примерно в 108 раз меньше средней скорости теплового движения <v>. Поэтому при вычислениях модуль результирующей скорости 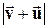 можно заменять модулем скорости теплового движения
можно заменять модулем скорости теплового движения 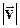 . Но среднее значение результирующей скорости
. Но среднее значение результирующей скорости 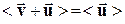 т.к.
т.к. 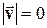 .
.
Лабораторная работа № 2.9
1. Перед включением установки поставить переключатели "Iэм" в положение "прям".
2. Подключить установку к сети. Перевести тумблер "Сеть" в положение "ВКЛ."
3. Передвигая ручку реостата "Iэм" добиться отсутствия тока в электромагните (контроль осуществлять по амперметру "Iэм").
4. Вращая потенциометр "Iдх", подать на датчик Холла максимальный ток (контроль осуществлять по амперметру "Iдх").
5. Потенциометром "Уст. 0" добиться отсутствия тока в гальванометре "Iг", что будет свидетельствовать расположению контактов под одним потенциалом. После этого потенциометром "Iдх" убрать ток с датчика Холла.
Рабочие формулы:
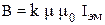 , (1)
, (1) 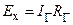 , (2)
, (2) 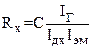 , (3)
, (3) 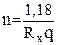 . (4)
. (4)
Данные для расчетов:
калибровочный коэффициент 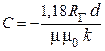 , m0 = 4p × 10–7 Гн/м, m = 500, k= 2,46 ×103 м–1, Rг = 4,4 кОм,
, m0 = 4p × 10–7 Гн/м, m = 500, k= 2,46 ×103 м–1, Rг = 4,4 кОм,
d = 4,0 ×10–4 м, s = 2,7 Ом–1м–1, q = 1,6 ×10-19 Кл.
Измерения:
При определении величины ЭДС Холла Ex для исключения напряжений, обусловленных побочными эффектами, измерение тока "Iг" необходимо проводить два раза при противоположных направлениях магнитного поля (положениях переключателя "Iэм": "прям." и "ОБР."),
а затем усреднять полученные значения: 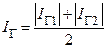 .
.
Задание № 1. Исследовать зависимость ЭДС Холла Ex от индукции магнитного поля B при постоянном значении тока Iдх, протекающего через образец.
Для этого установить ток в датчике Холла Iдх = 4 мА. Определить токи Iг, проходящие через гальванометр для 8-10 значений тока Iэм в электромагните (шаг изменения тока DIэм – 1-2 дел.). Для каждого из измерений, пользуясь формулами (1) и (2), вычислить B и Ex. Результаты измерений и вычислений занести в таблицу 1:
| № | Iэм, мА | В, Тл | Iдх = 4 мА | |||
| Iг1, мкА(прям) | Iг2, мкА(обр) | <Iг> мкА | Ex, В | |||
| … |
Построить график зависимости Ex=Ex(В) при Iдх= const.
Задание № 2. Исследовать зависимость ЭДС Холла Ex от величины силы тока Iдх, протекающего через образец, при постоянном значении индукции магнитного поля B (Iэм = const).
Установить ток в электромагните Iэм = 200 мА. Найти ток Iг, проходящий через гальванометр для 8-10 значений тока Iдх. Результаты измерений и вычислений занести в таблицу 2:
| № | Iдх, мА | Iэм = 200 мА | |||
| Iг1, мкА(прям.) | Iг2, мкА(обр.) | <Iг> мкА | Ex, В | ||
| … |
Построить график зависимости Ex=Ex(Iдх) при В = const.
Отключить установку от сети.
Задание № 3. На основании графических результатов и пользуясь формулами (3) и (4) вычислить постоянную Холла и концентрацию носителей тока. Проанализировать полученные результаты, пользуясь данными таблицы 3:
| Материалы | Rx, м3 Кл -1 | n, м -3 | s, Ом-1 м-1 | u0, м2 В-1 с-1 |
| Si Ge InSb InAs Bi GaAs | –102 –10–1 –5·10–4 –10–2 –5·10–8 –8·10–3 | 1022 1020 1022 1021 1026 1021 | 1,6·10-3 2,7 1,4·104 4,0·102 8,6·105 1,0·102 | 0,16 0,30 7,00 4,00 0,42 0,85 |
Можно ли на основании полученных данных рассчитать подвижность носителей заряда в образце?
Примечание.Отсчеты показаний осуществлять на основании таблицы рабочих характеристик приборов.
| Наименование прибора | Тип прибора | Пределы измерений | Цена деления | Класс точности |
| 1. Амперметр – "Iдх " | М284К | 0 – 5 мА | 200 мкА/дел. | 2,0 |
| 2. Амперметр – "Iэм " | М 284К | 0 – 250 мА | 10 мА/дел. | 2,0 |
| 3. Гальванометр – "Iг " | М 117/1 | ±50 мкА | 1 мкА/дел. | 0,5 |
