Елементи теорії відносності

· Постулати спеціальної теорії відносності (СТВ).

Перший постулат (принцип відносності): ніякі досліди, в тому числі і оптичні, проведені всередині інерціальної системи відліку не дають можливості виявити її рух. Це означає, що фізичні явища перебігають однаково в усіх інерціальних системах відліку, а фізичні закони інваріантні (мають однакову математичну форму запису) в різних інерціальних системах.

Другий постулат (принцип інваріантності швидкості). Швидкість світла у вакуумі не залежить від швидкості руху джерела світла чи спостерігача і однакова в усіх інерціальних системах відліку.

СТВ привела до повного перегляду класичних уявлень про простір і час, масу і енергію, які одержали надійне експериментальне підтвердження і тезисно представлені нижче.

· Якщо відомі просторово-часові координати 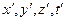події в “рухомій” системі координат 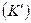, то її координати 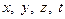в “нерухомій” системі 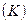можуть бути обчислені, використовуючи формули (перетворення Лоренца):

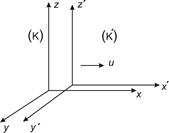
Рис. 5.1

, , ;

,

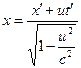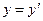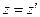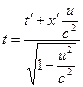де с – швидкість світла у вакуумі.

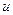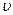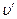· При взаємному віддаленні інерціальних систем (К) і (К') зі швидкістю швидкості тіла і зв’язані співвідношенням:

,

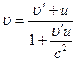а при зближенні: ,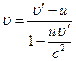

де 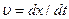, а .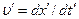

· Поздовжній розмір 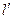тіла, що рухається зі швидкістю відносно деякої “нерухомої” системи відліку, зв’язаний з довжиною 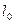тіла, нерухомого в цій системі співвідношенням:

,

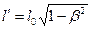де .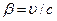

· Проміжок часу 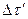між подіями в системі, що рухається зі швидкістю 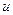по відношенню до спостерігача, зв’язаний з проміжком часу 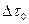між тими ж подіями в “нерухомій” системі співвідношенням:

.

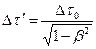· Маса тіла в процесі збільшення його швидкості зростає згідно з рівнянням:

,

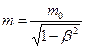де 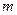– маса тіла, що рухається зі швидкістю 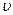, 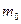– маса спокою цього тіла.

· Залежність кінетичної енергії тіла від швидкості дається рівнянням:

.

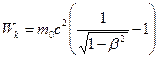· Зміні маси системи на величину 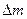відповідає зміна енергії системи на величину: .

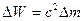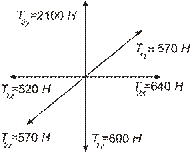5.1. У космічному кораблі встановлений прилад для вимірювання його прискорення. Він складається з кулі масою 100 кг, прикріпленої до шести струн, натягнених вздовж координатних осей системи відліку корабля. Натяги струн наведені на рис. 5.2. Знайти прискорення корабля. Якими причинами зумовлена несиметричність натягів струн. Чи є інерціальною система координат, зв’язана з кораблем ? Рис. 5.1

5.2. Одержати формулу розрахунку просторово-часових координат 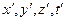(перетворень Лоренца) деякої події з системі 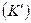при умові, якщо відомі її просторово-часові координати 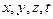в системі 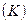та формули переходу від координат системи 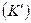до 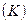, які наведені у вступі.

5.3. При якій швидкості руху тіла релятивістське скорочення його довжини становить 25 %?

5.4. Користуючись принципом відносності показати, що поперечні розміри тіла не міняються при переході від однієї системи відліку до іншої.

5.5. Знайти відносну похибку, що виникає при розрахунку, якщо замість релятивістського закону додавання швидкостей користуватись класичним.

5.6. Знайти відносне релятивістське скорочення розмірів елементарної частинки космічних променів, що має швидкість, яка дорівнює 95 % швидкості світла.

5.7. Яку швидкість повинно мати рухоме тіло, щоб його поздовжні розміри зменшились у два рази?

5.8. Іонізований атом, що вилетів з прискорювача зі швидкістю 0,8 с випустив фотон з напрямку свого руху. Визначити швидкість фотона відносно прискорювача, супроводжуючи розв’язок поясненнями.

5.9. Знайти вираз для густини тіла, що рухається зі швидкістю відносно “нерухомої” системи координат. Вважати, що густина тіла в “нерухомій” системі координат відома і дорівнює .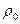

5.10. Швидкість світла в нерухомому прозорому середовищі дорівнює 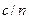, де 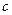– швидкість світла у вакуумі, 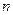– абсолютний показник заломлення речовини. Знайти швидкість, світла в середовищі, якщо воно: а) рухається назустріч джерелу світла з постійною швидкістю 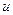; б) віддаляється від джерела світла зі швидкістю .

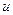5.11. Два прискорювачі викидають частинки назустріч одна одній зі швидкістю, що дорівнює 0,9 від швидкості світла у вакуумі. Визначити відносну швидкість зближення частинок з точки зору спостерігача, що рухається разом з однією із частинок.

5.12. На скільки відсотків зміняться поздовжні розміри протона і електрона після проходження ними різниці потенціалів ?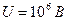

5.13. У скільки разів збільшиться тривалість існування нестабільної частинки (по годиннику спостерігача, зв’язаного з частинкою), якщо вона починає рухатись зі швидкістю, що становить 99 % швидкості світла?

5.14. Електрон прискорюється в електричному полі напруженістю 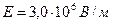: а) яка була б швидкість електрона через 1,0 нс, якби його маса не залежала від швидкості ? б) яка фактично швидкість електрона через 1,0 нс ?

5.15. Маса рухомого електрона вдвічі більша за його масу спокою. Знайти кінетичну енергію цього електрона.

5.16. Якою зміною маси супроводжується зменшення внутрішньої енергії тіла на один джоуль в процесі його охолодження? Чи можна його виявити, проводячи зважування тіла на аналітичних терезах, точність яких не перевищує 10^-2 мг?

5.17. Знайти втрату мас, що відбувається при утворенні одного кіломоля води згідно з реакцією:

.

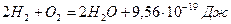5.18. При поділі ядра урану 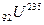звільнюється енергія, що дорівнює приблизно 200 МеВ. Знайти зміну маси при поділі одного кіломоля урану.

5.19. Сонце випромінює кожної хвилини енергію, що дорівнює 6,5·10²¹ кВт год. Вважаючи, що інтенсивність випромінювання Сонця з часом не змінюється, знайти, за який час маса Сонця зменшиться в два рази.

6. Механічні коливання і хвилі

· Вільні гармонічні коливання:

а) 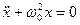– диференціальне рівняння коливань;

б) 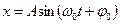, або 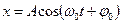– розв’язок рівняння,

де А – амплітуда коливань, 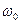– циклiчна частота коливань; 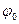– початкова фаза коливань;

в) 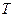– період коливань ( );

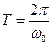г) 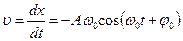– швидкість руху в коливному процесі,

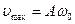– амплітуда швидкості;

д) 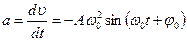– прискорення руху в коливному процесі,

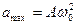– амплітуда прискорення;

е) 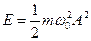– повна механічна енергія коливної системи.

· Загасаючі гармонічні коливання:

а) 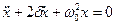– диференціальне рівняння коливань;

б) 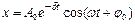– розв’язок рівняння;

де d – коефiцiєнт загасання, 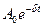– амплітуда коливань; 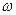– власна циклічна частота коливань ( ).

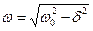в) 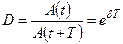– декремент загасання,

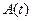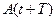де і – амплітуди двох послідовних коливань.

г) 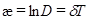– логарифмiчний декремент загасання;

д) 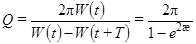– добротність коливальної системи,

де 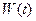та 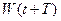– енергії коливальної системи в момент часу 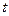і .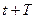

У випадку, коли 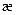<< 1, .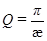

· Вимушені коливання:

а) 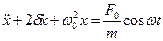– диференціальне рівняння коливань;

б) 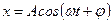– розв’язок рівняння,

де 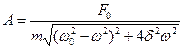– амплітуда вимушених коливань ( 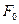– амплітуда вимушуючої сили);

в) 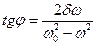– зсув фаз між зміщенням коливної точки і вимушуючою силою.

· Період коливань пружинного маятника:

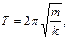
де m – маса тіла; k – жорсткість пружини.

· Період коливань математичного маятника:

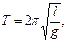
де l – довжина маятника; g – прискорення вільного падіння.

· Період коливань фізичного маятника:

,

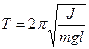де J – момент інерції маятника відносно точки його підвісу; 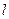– відстань між точкою підвісу і центром мас маятника.

· Довжина хвилі:

,

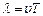де 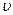– фазова швидкість поширення хвилі.

· Рівняння плоскої хвилі, яка поширюється вздовж осі 0Х:

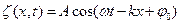
де k – хвильове число .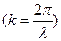

· Ефект Допплера: ,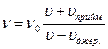

де 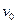– частота звукової хвилі, якщо джерело і приймач звукових хвиль нерухомі; 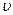– швидкість звуку; 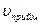– швидкість приймача; 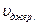– швидкість джерела звуку.

а) 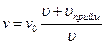– приймач рухається до джерела;

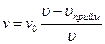– приймач рухається від джерела;

б) 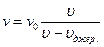– джерело рухається до приймача;

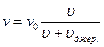– джерело рухається від приймача.

6.1. Рівняння коливань матеріальної точки має вигляд 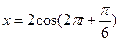м. Визначити зміщення цієї точки в початковий момент часу.

6.2. Визначити період коливань матеріальної точки, яка виконує гармонічні коливання за законом .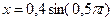

6.3. Визначити частоту гармонічних коливань, якщо амплітуда зміщення А,амплітуда швидкості .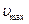

6.4. Матеріальна точка здійснює гармонічні коливання. Максимальна швидкість матеріальної точки 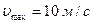, максимальне прискорення 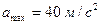. Визначити циклічну частоту коливань.

6.5. Матеріальна точка здійснює гармонічні коливання за синусоїдальним законом. У деякий момент часу її зміщення від положення рівноваги 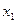=5 см. При збільшенні фази коливань в два рази зміщення точки стало 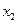=8 см. Визначити амплітуду коливань матеріальної точки.

6.6. Матеріальна точка масою 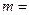10 г коливається за законом 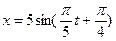. Визначити максимальну силу, яка діє на матеріальну точку.

6.7. Матеріальна точка масою 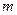виконує гармонічні коливання за законом 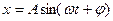. Визначити повну енергію коливальної точки.

6.8. Матеріальна точка починає рухатись вздовж осі 0Х так, що проекція її швидкості змінюється за законом 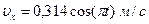. Визначити шлях, який пройде ця точка за 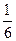с руху.

6.9. Матеріальна точка бере участь одночасно у двох коливаннях одного напрямку. Ці коливання є гармонічними з однаковими амплітудами й періодами коливань. Результуюче коливання має ту ж саму амплітуду і період коливань. Визначити початкову різницю фаз результуючого коливання.

6.10. Визначити амплітуду результуючого коливання, яке виникає при додаванні двох коливань одного напрямку:

, .

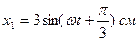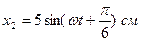6.11. Матеріальна точка бере участь у двох коливаннях одного напрямку, які виконуються за законом 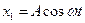i 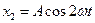. Визначити модуль максимальної швидкості матеріальної точки.

6.12. Матеріальна точка бере участь у двох взаємно перпендикулярних коливаннях з однаковими періодами та однаковими початковими фазами. Амплітуди коливань 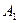= 3 см і 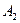= 4 см. Визначити амплітуду результуючого коливання.

6.13. Матеріальна точка бере участь одночасно в двох взаємно перпендикулярних коливаннях 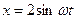і 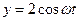. Визначити траєкторію руху матеріальної точки.

6.14. Матеріальна точка бере участь одночасно в двох взаємно перпендикулярних коливаннях 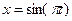і 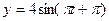. Визначити траєкторію руху матеріальної точки.

6.15. За час 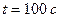система здійснює 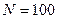коливань. За цей же час амплітуда коливань зменшилась у 2,718 раз. Визначити коефіцієнт загасання коливань, логарифмічний декремент загасання, добротність системи, відносне зменшення енергії 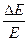системи за період коливань .

6.16. Мідна кулька, яка підвішена до пружини, виконує вертикальні коливання. Як зміниться період коливань, якщо до пружини підвісити алюмінієву кульку такого ж радіуса ?

6.17. Плоский айсберг товщиною 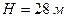при поштовху вниз коливається по вертикалі. Густина льоду 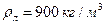, густина води 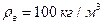. Визначити період коливань айсберга. Силою опору води знехтувати.

6.18. У відкриту з обох кінців U – подібну трубку з площею поперечного перерізу S швидко вливають ртуть масою m. Густина ртуті 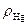. Визначити період коливань ртуті в трубці.

6.19. Маятниковий годинник ходить правильно при довжині маятника 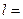55,8 см. На скільки відстане годинник за добу, якщо довжину збільшити на 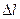= 0,5 см.

6.20. Маятниковий годинник перенесли з поверхні Землі на висоту H = 200 м. На скільки часу відстане цей годинник за добу?

6.21. Математичний маятник довжиною 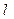= 24,7 см здійснює загасаючі коливання. Через який проміжок часу енергія коливань маятника зменшиться в 9,4 рази ? Логарифмічний декремент згасання 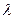= 0,01.

6.22. Амплітуда загасаючих коливань математичного маятника за 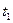=1 хв зменшилася вдвічі. У скільки разів вона зменшилася за 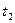= 3 хв ?

6.23. Амплітуда коливань математичного маятника за 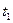=1 хв зменшилася вдвічі. Довжина маятника 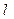= 1м. Визначити логарифмічний декремент загасання маятника.

6.24. Однорідний тонкий стрижень довжиною 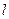= 1,2 м закріплений так, що він може обертатись навколо горизонтальної осі, яка проходить перпендикулярно до стрижня через один з його кінців. До середини та нижнього кінця стрижня прикріпили два однакові вантажі. Визначити зведену довжину та період коливань фізичного маятника. Масою стрижня знехтувати.

6.25. Що називають довжиною хвилі?

1. Віддаль, яку проходить тіло протягом одного періоду.

2. Віддаль між двома точками, які коливаються з різницею фаз.

3. Віддаль, яку проходить хвиля за одиницю часу.

4. Віддаль між двома сусідніми точками, які коливаються в однакових фазах.

6.26. Які з перерахованих хвиль називаються поздовжніми, а які поперечними?

1. Електромагнітні хвилі.

2. Звукові хвилі в газах.

3. Хвилі на поверхні води.

4. Звукові хвилі в рідинах.

6.27. Яку хвилю, поздовжню чи поперечну, описує рівняння ?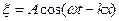

6.28. Чим визначається числове значення густини потоку енергії хвиль?

1. Енергією, яка переноситься хвилями через одиничну площину.

2. Енергією, яка переноситься хвилями за одиницю часу через одиничну площину.

3. Енергією, яка переноситься хвилями через дану площину.

4. Енергією, яка переноситься хвилями за одиницю часу через одиничну площину перпендикулярно до напрямку поширення хвиль.

5. Енергією, яка переноситься хвилями за одиницю часу через дану площину перпендикулярно до напрямку поширення хвиль.

6.29. Потік енергії хвиль через площину 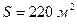, яка розміщена перпендикулярно до поширення хвиль, дорівнює 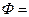0,11 Вт. Визначити густину потоку енергії при даних умовах.

6.30. Визначити швидкість поздовжньої пружної хвилі в мідному стрижні з модулем Юнга .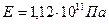

6.31. При деякому натягу струни довжиною 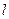= 1 м частота основного тону струни 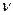=1000 Гц. Визначити швидкість поширення хвилі в струні.

6.32. Струна масою 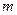закріплена з двох кінців. У ній збудили коливання циклічної частоти 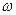з максимальною амплітудою 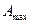. Визначити максимальну кінетичну енергію струни.

6.33. У пружному середовищі розповсюджується поздовжня плоска хвиля 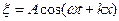. Намалювати для початкового моменту часу графіки залежності зміщення 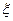від 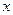і густини середовища 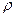від .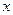

6.34. Рівняння плоскої хвилі, яка поширюється вздовж осі 0Х, має вигляд 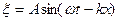. Зміщення від положення рівноваги точки, яка знаходиться на віддалі 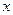= 4см від джерела коливань в момент час 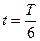, дорівнює половині амплітуди. Визначити довжину хвилі.

6.35. Визначити довжину стоячої хвилі, якщо віддаль між двома сусідніми пучностями дорівнює 0,5 м.

6.36. При якій мінімальній довжині скляної трубки, яка закріплена з однієї сторони, всередині неї може виникнути стояча хвиля?

6.37. Швидкість звуку в повітрі 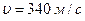. Визначити відстань на якій знаходяться дві найближчі точки, які здійснюють коливання в протилежних фазах, якщо частота коливань 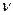= 170 Гц.

6.38. За який час звукові коливання пройдуть віддаль 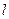між двома точками, якщо температура повітря між ними змінюється лінійно від 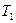до 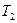. Швидкість звуку в повітрі 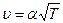, де 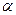– стала.

6.39. Нерухоме джерело випромінює у всіх напрямках звукову хвилю довжиною 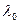. Як зміниться довжина хвилі, якщо джерело привести в рух із швидкістю, яка дорівнює половині швидкості звуку?

6.40. Джерело звукових коливань із частотою 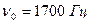і приймач знаходяться в одній точці. У початковий момент часу джерело починає віддалятися від приймача з постійним прискоренням 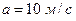. Швидкість звуку в повітрі 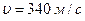. Визначити частоту коливань, яку сприймає нерухомий приймач через 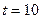с після початку руху джерела.