Пример 2. Частица массой m находится в одномерной прямоугольной потенциальной яме шириной с абсолютно непроницаемыми стенками

Частица массой m находится в одномерной прямоугольной потенциальной яме шириной 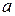с абсолютно непроницаемыми стенками. Получим допустимые значения энергии и импульса частицы.

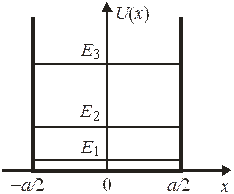
Классическая частица может иметь любую энергию в ящике с непроницаемыми стенками. Энергия квантовой частицы имеет дискретный спектр, зависящий от размеров потенциальной ямы.

Частица с полной энергией 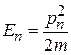внутри ямы при 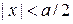имеет импульс

.

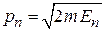Из условия квантования (1.17) для одномерного движения получаем

.

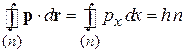С учетом перемещения вправо и влево, находим

, ,

,

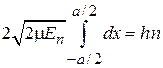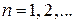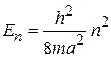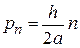. (П.1.3)

Чем уже яма и меньше масса частицы, тем больше интервал между соседними уровнями энергии.

Для основного состояния 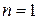с минимальной энергией из (П.1.3) получаем

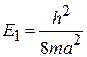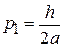, . (П.1.4)

Для электрона при L = 1 мм

.

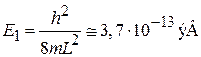Тепловая энергия kT такой величины соответствует температуре 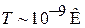. Следовательно, для частицы в макроскопическом объеме квантование энергии поступательного движения несущественно при достаточно высокой температуре.

Для микрообъема L = 1 нм получаем 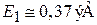, что превышает тепловую энергию 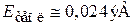при нормальной температуре. Следовательно, для частицы в микроскопическом объеме квантование энергии поступательного движения существенно при любой температуре. В результате микро- и наносистемы квантуются и требуют квантовомеханического описания.