Частотное представление детерминированных периодических сигналов

Кубанский государственный технологический университет

А.В.Власенко, В.И.Ключко

ТЕОРИЯ информациИ И
СИГНАЛОВ

Краснодар

Издательство КубГТУ

УДК.681. 32

А.В.Власенко, В.И.Ключко

Теория информации и сигналов. Учебное пособие / Краснодар: Изд-во КубГТУ, 2001.- 147 с.

ISBN 5-230-21895-9

Изложены основные математические и информационные модели сигналов и каналов связи и рассмотрены методы преобразования сигналов и эффективного кодирования информации.

Описываются линейные систематические коды, а также методы их построения и декодирования. Проанализирована эффективность различных систем передачи и обработки информации, использующих помехоустойчивые
коды.

Показано влияние методов фильтрации помех и различных критериев принятия решений при идентификации сигналов на качество передачи сообщений.

Предназначено для студентов специальностей 220400 и 351400, а также для аспирантов кафедры ВТ и АСУ.

Табл. 3. Ил. 20. Библиогр.: 3 назв.

Печатается по решению Редакционно-издательского совета Кубанского государственного технологического университета

Рецензенты: зав. каф. СА и ОИ д-р экон. наук, проф.

Т.П. Барановская (КГАУ),

проф. каф. ВТ и АСУ д-р техн. наук, проф.

В.И. Лойко (КубГТУ).

с- (22.04) @ Кубанский государственный

ISBN 5-230-21895-9 технологический университет, 2003

ВВЕДЕНИЕ

Роль информации в современном обществе непрерывно возрастает. Информационные процессы являются обязательной составляющей производства, экономики, науки, военного дела и общественной жизни. Поэтому важным является осознание сущности понятия информации и рассмотрение математических моделей для количественной оценки информации. Так как в основе формализованного подхода находятся вероятностные понятия, то естественные информационные процессы характеризуются избыточностью. Это требует рассмотрения эффективных методов кодирования, позволяющих за счет использования неравномерных кодов сжать информацию, исключив избыточность. Закодированная таким образом информация эффективна по занимаемому объему памяти и по скорости передачи и обработки, но очень чувствительна к помехам, которые могут привести к ее искажению, поэтому необходимым условием ее достоверной передачи или обработки является целенаправленное избыточное (помехоустойчивое) кодирование, позволяющее обнаруживать и исправлять ошибки заданной кратности. Эти вопросы рассматриваются на примере линейных систематических кодов и самой известной их реализацией - циклических кодах.

Так как информация может передаваться на значительные расстояния только при помощи сигналов, рассматриваются основные математические модели и характеристики сигналов, а также методы их преобразования и оптимального приема.

Анализ эффективности и помехоустойчивость осуществляется для систем передачи и обработки информации, реализующих различные алгоритмы работы.

Математическое описание сигналов и помех

Структурная схема системы передачи информации. Основные понятия и определения

Под системой передачи информации (рисунок 1.1) будем понимать комплекс устройств, обеспечивающих передачу сообщений от источника (И) получателю (П). Сообщением называется то, что подлежит передаче (статический во времени ансамбль символов, расположенных определенным образом в пространстве). Сообщение передается посредством сигналов (материальных носителей). Принципиальное отличие сигнала от сообщения состоит в том, что сигнал временной процесс, что обусловлено методом формирования сигнала - разверткой. Сигнал – изменяющаяся физическая величина. Рассматривать будем только электрические сигналы.

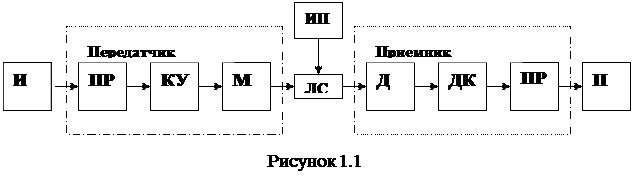Сообщение от источника поступает в передатчик, где преобразуется (ПР - преобразователь) в электрические сигналы. Эти сигналы, как правило, являются низкочастотным и они не используются для непосредственной передачи на расстояние. Сообщение в виде электронного воздействия (сигналов) поступает на вход кодирующего устройства (КУ), где оно преобразуется во вторичный сигнал.

Под кодированием будем понимать построение набора сигналов по определенным правилам, которое соответствует некоторой математической модели, обеспечивающей защиту передаваемой информации от ошибок. С кодирующего устройства сигнал поступает в модулятор (М), который преобразует исходный сигнал в высокочастотный сигнал по закону изменения сообщения. Такое преобразование называется модуляцией и оно обеспечивает лучшие условия передачи сигнала по линии связи (ЛС) при воздействии на сигнал помех (ИП - источник помех). Из линии связи искаженный сигнал поступает на вход приемника, где подвергается демодуляции (Д) - преобразованию, обратному модуляции и декодированию (ДК)-преобразованию, обратному кодированию. При декодировании обнаруживаются и исправляются ошибки в сообщении, появившиеся от воздействия помех. На заключительном этапе сигнал преобразуется (ПР) в сообщение, которое выдается получателю (П).

Классификация сигналов

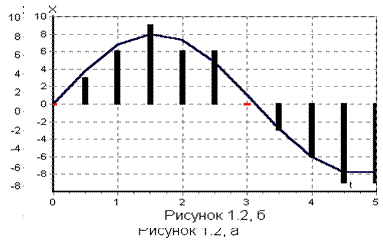Все сообщения по характеру изменения во времени можно разделить на непрерывные и дискретные(рисунок 1.2). Непрерывные сообщения отображаются непрерывной функцией времени, а дискретные сообщения – дискретной функцией времени. Аналогично сообщения могут быть непрерывными и дискретными по множеству значений. Соответствующую классификацию имеют и электрические сигналы, отображающие рассмотренные сообщения (рисунок 1.2):

а – сигнал, непрерывный по времени и по множеству и непрерывный по времени и дискретный по множеству;

б - сигнал, дискретный по времени и по множеству.

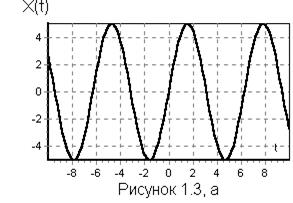
По своей структуре сигналы могут быть простымиисложными(рисунок 1.3). В качестве простых сигналов используются радиоимпульсы (а).

Сложный (составной) сигнал состоит из нескольких простых сигналов (б).

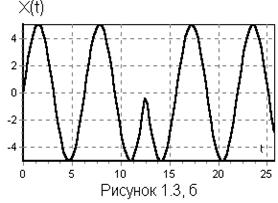
Основным свойством, характеризующим любое сообщение, является его случайный характер.

Детерминированность предполагает известность функции (в том числе и функции времени) и не требует передачи значений этой функции.

Тогда сообщение может быть представлено в виде случайного сигнала, а случайный сигнал в свою очередь может быть сформирован из простых детерминированных сигналов.

Следовательно, прежде всего, возникает задача исследования и описания детерминированных и случайных сигналов.

Детерминированный сигнал считается заданным, если известна функция X(t) данного сигнала и задан интервал, на котором действует сигнал.

Пример: X(t) = A sin wt; X(t) = B e^-ct; и др.

На рисунках 1.2 и 1.3 изображено временное представление сигналов. При этом возможно указать длительность сигнала T_c, его максимальное значение A_max и его минимальное значение A_min.

Вторая форма представления сигналов – частотная.

Частотное представление детерминированных периодических сигналов

При анализе систем передачи информации широко используются синусоидальные сигналы.

В связи с этим большой интерес имеет частотное представление сигнала, т.е. представление модели сигнала в виде совокупности элементарных синусоидальных сигналов.

В частотном виде могут представляться как периодические, так и непериодические детерминированные сигналы. Необходимо заметить, что в реальных условиях «чисто» периодические сигналы не существуют, т.к. идеальный периодический сигнал бесконечен во времени, в то время как всякий реальный сигнал имеет начало и конец. Однако во многих случаях конечностью времени действия сигнала можно пренебречь и для его анализа допустимо использовать аппарат, пригодный для идеальных периодических сигналов.

Периодические сигналы.

Рассмотрим сигнал, выражаемый произвольной периодической функцией времени X(t) (рисунок 1.4, а).

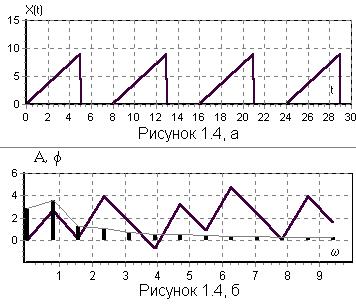
Известно, что всякая периодическая функция, удовлетворяющая условиям Дирихле (функция ограничена, кусочно-непрерывная и имеет конечное число экстремумов на протяжении периода), может быть представлена в виде бесконечной суммы гармонических составляющих.

Известны две формы разложения в ряд Фурье: тригонометрическая и комплексная.

Тригонометрическая форма разложения выражается в виде

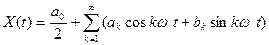, (1.1)

где

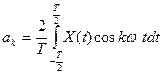[k=0,1,2,3…¥], (1.2)

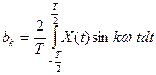[k=1,2,3…¥], (1.3)

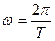- круговая частота;

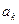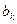, - амплитуды синусоидальных и косинусоидальных составляющих гармонических колебаний;

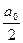- постоянная составляющая.

Представив гармонические составляющие в векторной форме, оказывается возможным перейти ко второму виду тригонометрической формы разложения.

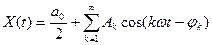, (1.4)

где 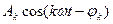-k-я гармоническая составляющая;

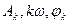- амплитуда, частота и начальная фаза k-ой гармонической составляющей (рисунок 1.4, б);

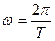- частота основной (первой) гармонии;

T - период колебаний.

В этом случае

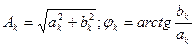(1.5)

В математическом отношении удобнее оперировать комплексной формой ряда Фурье, представляемой в виде

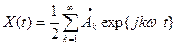, (1.6)

где 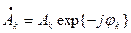- комплексная амплитуда гармонической составляющей частоты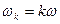

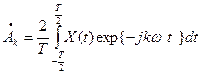. (1.7)

При этом модуль комплексной амплитуды будет равен амплитуде соответствующей гармонической составляющей, а аргумент равен начальной фазе составляющей.

Совокупность амплитуд и соответствующих частот гармоник принято называть спектром амплитуд, а совокупность начальных фаз и соответствующих частот гармоник называют спектром фаз (рисунок 1.4 б). Спектр амплитуд и спектр фаз однозначно определяют сигнал, однако для многих практических задач достаточно ограничиться спектром амплитуд. Отдельные спектральные составляющие в графическом изображении спектра амплитуд называют спектральными линиями.

Характерной особенностью спектра периодического сигнала является его прерывистость (дискретность). Расстояние между соседними спектральными линиями одинаковое и равно частоте основной гармоники.

Примечание: преобразование тригонометрической формы разложения в комплексную форму определяется формулой Эйлера.

,

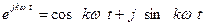из которой следует ,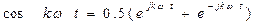

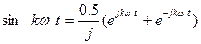
Подставляя эти выражения в (1.1), получим

,

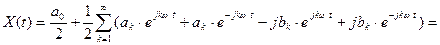
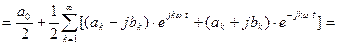
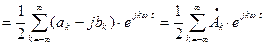что и требовалось доказать. 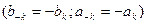.