Где V – объем соленоида, n – число витков на единицу длины соленоида.
Мгновенное значение сила тока в цепи, обладающей сопротивлением R и индуктивностью L: 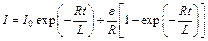 .
.
Энергия магнитного поля: 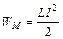 .
.
Объемная плотность энергии магнитного поля:
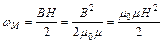 .
.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
1. В углах при основании равнобедренного треугольника с боковой стороной 8 см расположены заряды Q1 и Q2. Определить силу, действующую на заряд Q2 равный 1нКл, помещенный в третью вершину треугольника, угол при которой 120°. Рассмотреть случаи: а) Q1= Q2 = 2 нКл; б) ½Q1½=½-Q2 ½= 2 нКл.
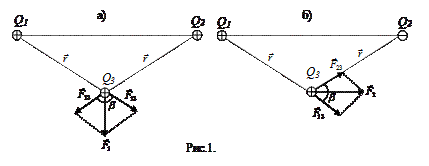
Решение. В соответствии с принципом суперпозиции поле каждого из зарядов Q1 и Q2 действует на заряд Q3 независимо. Это значит, что на заряд Q3 действуют силы (рис. 1, а): 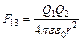 ,
, 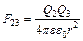 . Так как
. Так как 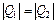 , то
, то 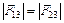 . Векторная сумма
. Векторная сумма 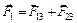 является искомой величиной. Модуль силы определяется по теореме косинусов
является искомой величиной. Модуль силы определяется по теореме косинусов 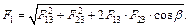 В случае одноименных зарядов Q1 и Q2 из рис.1, а видно, что угол b = 120°, поэтому F1 = F13 = F23:
В случае одноименных зарядов Q1 и Q2 из рис.1, а видно, что угол b = 120°, поэтому F1 = F13 = F23: 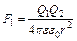 . F1=2,8×10-6 Н.
. F1=2,8×10-6 Н.
В случае разноименных зарядов Q1 и Q2 из рис.1,б видно, что угол b = 60° и, следовательно, 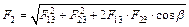 ,
,
F2=4,8×10-6 Н.
 Ответ: F1=2,8×10-6 Н, F2= 4,8×10-6 Н.
Ответ: F1=2,8×10-6 Н, F2= 4,8×10-6 Н.
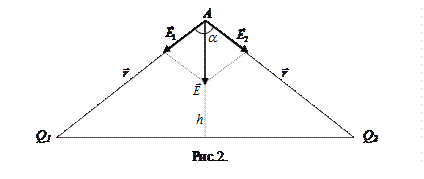
2. Два равных отрицательных заряда по 9 нКл находятся в воде на расстоянии l=8 см друг от друга. Определить напряженность и потенциал поля в точке, расположенной на расстоянии h=5 см от линии, соединяющей заряды.
Решение. Напряженность поля, создаваемого в точке А (рис.2) зарядами Q1 и Q2 по принципу суперпозиции полей, равна векторной сумме напряженностей, создаваемых каждым из зарядов:
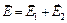 . (1)
. (1)
 По теореме косинусов:
По теореме косинусов: 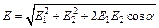 . (2)
. (2)
Напряженность поля точечного заряда Q: 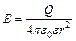 , где
, где  – диэлектрическая проницаемость;
– диэлектрическая проницаемость; 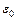 – электрическая постоянная;
– электрическая постоянная; 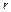 – расстояние от заряда до точки поля, в которой определяется его напряженность. Заряды Q1 и Q2 отрицательны, следовательно, векторы
– расстояние от заряда до точки поля, в которой определяется его напряженность. Заряды Q1 и Q2 отрицательны, следовательно, векторы 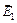 и
и 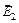 направлены к зарядам. По условию заряды Q1 = Q2 расположены на одинаковом расстоянии от точки А, поэтому Е1 = Е2. Следовательно, формула (2) принимает вид Е = 2Е1×cos
направлены к зарядам. По условию заряды Q1 = Q2 расположены на одинаковом расстоянии от точки А, поэтому Е1 = Е2. Следовательно, формула (2) принимает вид Е = 2Е1×cos 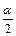 , где cos
, где cos 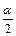 = h/r,
= h/r, 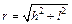 . Тогда напряженность в точке А:
. Тогда напряженность в точке А: 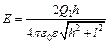 , E = 480 В/м. Потенциал
, E = 480 В/м. Потенциал  , создаваемый системой точечных зарядов в данной точке поля, равен алгебраической сумме потенциалов полей, создаваемых этими зарядами:
, создаваемый системой точечных зарядов в данной точке поля, равен алгебраической сумме потенциалов полей, создаваемых этими зарядами: 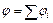 . Потенциал
. Потенциал 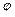 результирующего поля в точке А равен:
результирующего поля в точке А равен: 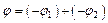 . Потенциал поля, создаваемого точечным зарядом,
. Потенциал поля, создаваемого точечным зарядом, 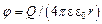 . Следовательно,
. Следовательно, 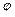 = - 40 В.
= - 40 В.
Ответ: Е = 480 В/м; 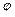 = - 40 В.
= - 40 В.
3. Заряд 1 нКл переносится в воздухе из точки, находящейся на расстоянии 1 м от бесконечно длиной равномерно заряженной нити, в точку на расстоянии 10 см от нее. Определить работу, совершаемую против сил поля, если линейная плотность заряда нити 1 мкКл/м. Какая работа совершается на последних 10 см пути?
Решение. Работа внешней силы по перемещению заряда Q из точки поля с потенциалом 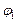 в точку с потенциалом
в точку с потенциалом 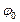 равна:
равна: 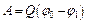 . (1)
. (1)
Бесконечная равномерно заряженная нить с линейной плотностью заряда t создает аксиально-симметричное поле напряженностью 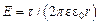 . Напряженность и потенциал этого поля связаны соотношением
. Напряженность и потенциал этого поля связаны соотношением 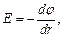 откуда
откуда 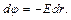 Разность потенциалов точек поля на расстоянии
Разность потенциалов точек поля на расстоянии 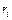 от нити:
от нити: 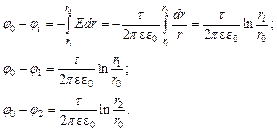 (2)
(2)
Подставляя в формулу (1) найденное выражение для разности потенциалов из (2), определим работу, совершаемую внешними силами по перемещению заряда из точки, находящейся на расстоянии 1 м, до точки, расположенной на расстоянии 0,1 м от нити: 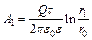 , A1 = 4,1×10-5 Дж. Работа по перемещению заряда на последних 10 см пути равна:
, A1 = 4,1×10-5 Дж. Работа по перемещению заряда на последних 10 см пути равна: 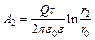 , A2 = 1,25×10-5 Дж.
, A2 = 1,25×10-5 Дж.
Ответ: А1 = 4,1×10-5 Дж; А2 = 1,25×10-5Дж.
4. К одной из обкладок плоского конденсатора прилегает стеклянная плоскопараллельная пластинка (e=7) толщиной 9 мм. После того как конденсатор отключили от источника напряжения 220 В и вынули стеклянную пластинку, между обкладками установилась разность потенциалов 976 В. Определить зазор между обкладками и отношение конечной и начальной энергии конденсатора.
Решение. После отключения конденсатора и удаления стеклянной пластинки заряд на его обкладках остается неизменным, т.е. выполняется равенство: 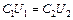 . (1)
. (1)
где С1 и С2 – электроемкости конденсатора в начальном и конечном случае. По условию конденсатор вначале является слоистым и его электроемкость определяется по формуле: 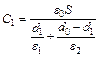 , (2)
, (2)
где S – площадь обкладок; d0 – зазор между ними, d1 – толщина стеклянной пластинки; ε1 и ε2 – диэлектрические проницаемости стекла и воздуха соответственно. После удаления стеклянной пластинки электроемкость конденсатора: 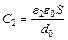 . (3)
. (3)
Подставляя (2) и (3) в (1), получим: 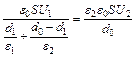 , откуда
, откуда 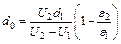 ,
, 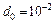 м. Начальная и конечная энергии конденсатора:
м. Начальная и конечная энергии конденсатора: 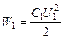 ,
, 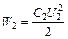 . Тогда отношение этих энергий:
. Тогда отношение этих энергий: 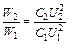 . Учитывая (1), получим:
. Учитывая (1), получим: 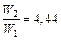 .
.
Ответ: d0 = 10-2 м; W2/W1 = 4,44.
5. Батарею из двух конденсаторов емкостью 400 и 500 пФ соединили последовательно и включили в сеть с напряжением 220 В. Потом батарею отключили от сети, конденсаторы разъединили и соединили параллельно обкладками, имеющими одноименные заряды. Каким будет напряжение на зажимах полученной батареи?
Решение. У последовательно соединенных конденсаторов заряды на обкладках равны по модулю Q1 = Q2 = Q и заряд батареи равен заряду одного конденсатора. Емкость батареи последовательно соединенных конденсаторов определяется по формуле: 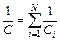 . Для батареи из двух конденсаторов:
. Для батареи из двух конденсаторов: 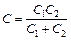 , а их заряд:
, а их заряд: 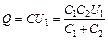 . (1)
. (1)
При отключении конденсаторов их заряд сохраняется. У параллельно соединенных конденсаторов заряд батареи равен сумме зарядов конденсаторов Q' = Q1 + Q2, а емкость сумме емкостей: 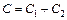 . Напряжение на зажимах батареи из двух параллельно соединенных конденсаторов:
. Напряжение на зажимах батареи из двух параллельно соединенных конденсаторов: 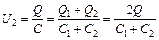 . (2)
. (2)
Подставляя (1) в (2), получаем: 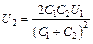 ,
, 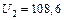 В.
В.
Ответ: 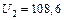 В.
В.
6. Заряд конденсатора 1 мкКл, площадь пластин 100 см2, зазор между пластинками заполнен слюдой. Определить объемную плотность энергии поля конденсатора и силу притяжения пластин.
Решение. Сила притяжения между двумя разноименно заряженными обкладками конденсатора: 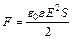 , (1)
, (1)
где Е – напряженность поля конденсатора; S – площадь обкладок конденсатора; ε – диэлектрическая проницаемость слюды; ε0 – электрическая постоянная. Напряженность однородного поля плоского конденсатора: 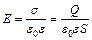 , (2)
, (2)
где 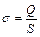 – поверхностная плотность заряда. Подставляя (2) в (1), получаем:
– поверхностная плотность заряда. Подставляя (2) в (1), получаем: 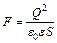 ,
, 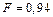 Н. Объемная плотность энергии электрического поля:
Н. Объемная плотность энергии электрического поля: 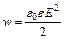 . (3)
. (3)
Подставляя (2) в (3), получаем: 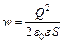 ,
, 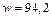 Дж/м3.
Дж/м3.
Ответ: 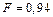 Н,
Н, 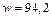 Дж/м3.
Дж/м3.
7. В медном проводнике сечением 6 мм и длиной 5 м течет ток. За 1 мин в проводнике выделяется 18 Дж теплоты. Определить напряженность поля, плотность и силу электрического тока в проводнике.
Решение. Для решения задачи используем законы Ома и Джоуля-Ленца. Закон Ома в дифференциальной форме имеет вид: 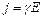 , (1)
, (1)
где j – плотность тока; Е – напряженность поля; γ – удельная проводимость. Закон Джоуля-Ленца: 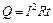 , (2)
, (2)
здесь I – сила тока, t – время. 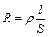 – сопротивление проводника, где r, l, S – удельное сопротивление, длина и площадь поперечного сечения проводника соответственно. Силу тока находим из (2):
– сопротивление проводника, где r, l, S – удельное сопротивление, длина и площадь поперечного сечения проводника соответственно. Силу тока находим из (2): 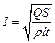 ,
, 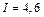 А. По определению, плотность тока равна:
А. По определению, плотность тока равна: 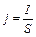 ,
, 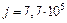 А/м2. Напряженность поля в проводнике определим из (1), учитывая, что
А/м2. Напряженность поля в проводнике определим из (1), учитывая, что 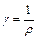 .
. 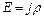 ,
, 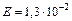 В/м.
В/м.
Ответ: 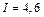 А,
А, 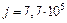 А/м2,
А/м2, 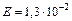 В/м.
В/м.
8. Внутреннее сопротивление аккумулятора 2 Ом. При замыкании его одним резистором сила тока равна 4 А, при замыкании другим – 2 А. Во внешней цепи в обоих случаях выделяется одинаковая мощность. Определить электродвижущую силу аккумулятора и внешние сопротивления.
Решение. Закон Ома для замкнутой (полной) цепи имеет вид:
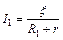 ,
, 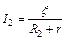 , (1)
, (1)
где r – внутреннее сопротивление источника тока; ξ – э.д.с. аккумулятора; R1 и R2 – внешние сопротивления цепей. Уравнения (1) представим в виде:
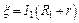 ,
, 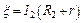 . (2)
. (2)
Из равенства (2) следует, что:
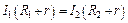 . (3)
. (3)
Мощность, выделяемая во внешней цепи в первом и втором случаях, cоответственно равна: 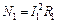 и
и 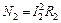 . Из условия равенства мощностей следует, что:
. Из условия равенства мощностей следует, что:
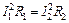 . (4)
. (4)
Решая совместно уравнения (3) и (4), получаем:
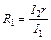 и
и 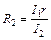 . (5)
. (5)
Подставляя (5) в (2), получаем: 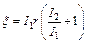 ,
, 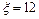 В,
В, 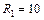 Ом,
Ом, 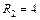 Ом.
Ом.
Ответ: 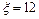 В,
В, 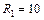 Ом,
Ом, 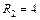 Ом.
Ом.
9. Электродвижущая сила батареи равна 20 В. Коэффициент полезного действия батареи составляет 0,8 при силе тока 4 А. Чему равно внутреннее сопротивление батареи?
Решение. Коэффициент полезного действия источника тока η равен отношению падения напряжения во внешней цепи к его электродвижущей силе: 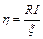 , откуда
, откуда 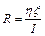 . Используя выражение закона Ома для замкнутой цепи
. Используя выражение закона Ома для замкнутой цепи 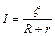 , получаем
, получаем 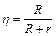 . Тогда
. Тогда 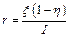 и
и 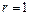 Ом.
Ом.
Ответ: 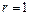 Ом.
Ом.
10. По двум бесконечно длинным прямолинейным проводникам, находящимся на расстоянии 50 см друг от друга, в одном направлении текут токи 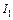 и
и 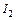 силой по 5 А. Между проводниками на расстоянии 30 см от первого расположен кольцевой проводник с током
силой по 5 А. Между проводниками на расстоянии 30 см от первого расположен кольцевой проводник с током 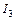 силой 5 А. Радиус кольца 20 см. Определить индукцию и напряженность магнитного поля, создаваемого токами в центре кольцевого проводника.
силой 5 А. Радиус кольца 20 см. Определить индукцию и напряженность магнитного поля, создаваемого токами в центре кольцевого проводника.
Решение. В соответствии с принципом суперпозиции индукция результирующего магнитного поля в точке А равна: 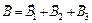 , где
, где 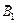 и
и 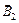 – индукции полей, создаваемых соответственно токами
– индукции полей, создаваемых соответственно токами 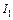 и
и 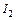 , направленными за плоскость рисунка;
, направленными за плоскость рисунка; 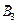 – индукция поля, создаваемая кольцевым током. Векторы
– индукция поля, создаваемая кольцевым током. Векторы 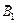 и
и 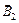 направлены по одной прямой в противоположные стороны, поэтому их сумма
направлены по одной прямой в противоположные стороны, поэтому их сумма 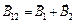 равна по модулю:
равна по модулю: 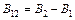 . Индукция поля, создаваемого бесконечно длинным проводником с током:
. Индукция поля, создаваемого бесконечно длинным проводником с током: 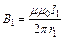 и
и 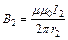 . Тогда
. Тогда 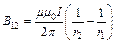 . Индукция поля, создаваемого кольцевым проводником с током:
. Индукция поля, создаваемого кольцевым проводником с током: 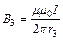 , где r3 – радиус кольца. Векторы
, где r3 – радиус кольца. Векторы 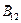 и
и 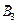 взаимно перпендикулярны, поэтому:
взаимно перпендикулярны, поэтому: 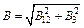 или
или 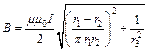 ,
, 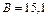 мкТл. Напряженность магнитного поля:
мкТл. Напряженность магнитного поля: 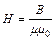 и
и 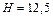 А/м.
А/м.
Ответ: 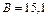 мкТл,
мкТл, 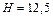 А/м.
А/м.
11. Электрон, пройдя ускоряющую разность потенциалов 88 кВ, влетает в однородное магнитное поле перпендикулярно его линиям индукции. Индукция поля равна 0,01 Тл. Определить радиус траектории электрона.
Решение. В магнитном поле на электрон, движущийся со скоростью 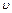 перпендикулярно
перпендикулярно 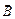 , действует сила Лоренца:
, действует сила Лоренца: 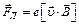 , которая обусловливает центростремительное ускорение электрона при его движении по окружности:
, которая обусловливает центростремительное ускорение электрона при его движении по окружности: 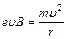 , где m – масса электрона; е – его заряд; r – радиус траектории его движения. Пройдя ускоряющую разность потенциалов U, электрон приобретает кинетическую энергию, равную работе А сил электрического поля:
, где m – масса электрона; е – его заряд; r – радиус траектории его движения. Пройдя ускоряющую разность потенциалов U, электрон приобретает кинетическую энергию, равную работе А сил электрического поля: 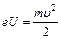 . Отсюда находим скорость электрона:
. Отсюда находим скорость электрона: 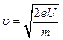 . Зная ее, найдем радиус траектории:
. Зная ее, найдем радиус траектории: 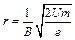 и
и 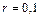 м.
м.
Ответ: 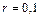 м.
м.
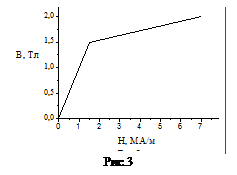 12. Соленоид длиной 20 см и диаметром 4 см имеет плотную трехслойную обмотку из провода диаметром 0,1 мм. По обмотке соленоида течет ток 0,1 А. Зависимость B = f(H) для материала сердечника приведена на рис. 3. Определить напряженность и индукцию поля в соленоиде, магнитную проницаемость сердечника, индуктивность соленоида, энергию и объемную плотность энергии поля соленоида.
12. Соленоид длиной 20 см и диаметром 4 см имеет плотную трехслойную обмотку из провода диаметром 0,1 мм. По обмотке соленоида течет ток 0,1 А. Зависимость B = f(H) для материала сердечника приведена на рис. 3. Определить напряженность и индукцию поля в соленоиде, магнитную проницаемость сердечника, индуктивность соленоида, энергию и объемную плотность энергии поля соленоида.
Решение. Поле внутри соленоида можно считать однородным. В этом случае напряженность поля: 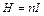 , где
, где 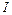 – сила тока в обмотке;
– сила тока в обмотке; 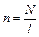 число витков, приходящихся на единицу длины соленоида. Тогда:
число витков, приходящихся на единицу длины соленоида. Тогда: 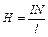 и
и 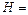 300А/м. По графику В = f(H) находим, что напряженности 3000 А/м соответствует индукция 1,7 Тл. Используя связь между индукцией и напряженностью:
300А/м. По графику В = f(H) находим, что напряженности 3000 А/м соответствует индукция 1,7 Тл. Используя связь между индукцией и напряженностью: 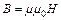 , определим магнитную проницаемость:
, определим магнитную проницаемость: 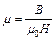 и
и 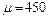 . Индуктивность соленоида:
. Индуктивность соленоида: 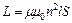 , где l – длина,
, где l – длина, 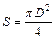 – площадь поперечного сечения соленоида. Получаем:
– площадь поперечного сечения соленоида. Получаем: 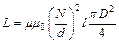 . Объемная плотность энергии магнитного поля:
. Объемная плотность энергии магнитного поля: 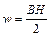 и
и 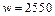 Дж/м3. Энергия магнитного поля соленоида:
Дж/м3. Энергия магнитного поля соленоида: 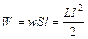 и
и 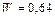 Дж.
Дж.
Ответ: В =1,7 Тл, Тл. 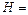 3000 А/м,
3000 А/м, 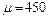 ,
, 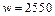 Дж/м3,
Дж/м3, 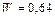 Дж.
Дж.
13. На соленоид (см. условие и решение задачи 12) надето изолированное кольцо того же диаметра. Определить электродвижущую силу индукции в кольце и электродвижущую силу самоиндукции в соленоиде, если за 0,01 с ток в его обмотке равномерно снижается до нуля.
Решение. По условию за время ∆t = 0,01 с сила тока в обмотке соленоида равномерно уменьшается от 0,1 А до нуля, поэтому магнитный поток, пронизывающий площадь кольца 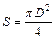 , уменьшается от
, уменьшается от 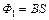 до
до 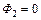 . Электродвижущая сила индукции, возникающая в кольце:
. Электродвижущая сила индукции, возникающая в кольце: 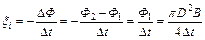 и
и 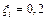 B. Электродвижущая сила самоиндукции ξS , возникающая в соленоиде при выключении тока в нем:
B. Электродвижущая сила самоиндукции ξS , возникающая в соленоиде при выключении тока в нем: 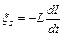 . Так как при выключении сила тока уменьшается до нуля равномерно, то:
. Так как при выключении сила тока уменьшается до нуля равномерно, то: 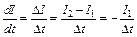 . Тогда:
. Тогда: 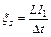 и
и 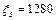 В.
В.
Ответ: 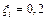 B,
B, 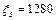 В.
В.
14. Виток радиусом 5 см с током 1 А помещен в однородное магнитное поле напряженностью 5000 А/м так, что нормаль к витку составляет угол 60° с направлением поля. Какую работу совершат силы поля при повороте витка в устойчивое положение?
Решение. Работа А при повороте витка с током 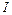 в магнитном поле:
в магнитном поле: 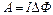 . Здесь
. Здесь 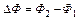 – изменение магнитного потока сквозь площадь витка
– изменение магнитного потока сквозь площадь витка 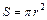 ;
; 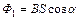 – магнитный поток, пронизывающий виток в начальном положении, где α – угол между векторами
– магнитный поток, пронизывающий виток в начальном положении, где α – угол между векторами 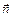 и
и 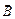 . Устойчивым положением витка в магнитном поле является такое, при котором направление нормали к нему совпадает с вектором индукции, т. е.
. Устойчивым положением витка в магнитном поле является такое, при котором направление нормали к нему совпадает с вектором индукции, т. е. 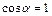 . Следовательно,
. Следовательно, 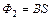 . Таким образом,
. Таким образом, 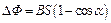 . Учитывая, что
. Учитывая, что 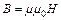 , имеем:
, имеем: 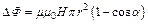 . Окончательно имеем:
. Окончательно имеем: 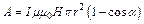 и
и 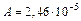 Дж.
Дж.
Ответ: 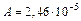 Дж.
Дж.
КОНТРОЛЬНАЯ РАБОТА № 2
201. В вершинах квадрата со стороной 0,1 м расположены равные одноименные заряды. Потенциал создаваемого ими поля в центре квадрата равен 500 В. Определить заряд.
202. В вершинах квадрата со стороной 0,5 м расположены заряды одинаковой величины. В случае, когда два соседних заряда положительные, а два других – отрицательные, напряженность поля в центре квадрата равна 144 В/м. Определить величину зарядов.
203. В вершинах квадрата со стороной 0,1 м помещены заряды по 0,1 нКл. Определить напряженность и потенциал поля в центре квадрата, если один из зарядов отличается по знаку от остальных.
204. Пространство между двумя параллельными бесконечными плоскостями с поверхностной плотностью зарядов +5∙10-8 и -9∙10-8 Кл/м2 заполнено стеклом. Определить напряженность поля: а) между плоскостями; б) вне плоскостей.
205. На расстоянии 8 см друг от друга в воздухе находятся два заряда по 1 нКл. Определить напряженность и потенциал поля в точке, находящейся на расстоянии 5 см от зарядов.
206. Две параллельные плоскости одноименно заряжены и имеют поверхностную плотность зарядов 2 и 4 нКл/м2. Определить напряженность поля: а) между плоскостями; б) вне плоскостей.
207. Если в центр квадрата, в вершинах которого находятся заряды по +2 нКл, поместить отрицательный заряд, то результирующая сила, действующая на каждый заряд, будет равна нулю. Вычислить числовое значение отрицательного заряда.
208. Заряды по 1 нКл помещены в вершинах равностороннего треугольника со стороной 0,2 м. Равнодействующая сил, действующих на четвертый заряд, помещенный на середине одной из сторон треугольника, равна 0,6 мкН. Определить этот заряд, напряженность и потенциал поля в точке его расположения.
209. Два шарика массой по 0,2 г подвешены в общей точке на нитях длиной 0,5 м. Шарикам сообщили заряд и нити разошлись на угол 90°. Определить напряженность и потенциал поля в точке подвеса шарика.
210. Два одинаковых заряда находятся в воздухе на расстоянии 0,1 м друг от друга. Напряженность поля в точке, удаленной на расстоянии 0,06 м от одного и 0,08 м от другого заряда, равна 10 кВ/м. Определить потенциал поля в этой точке и значение зарядов.
211. Пылинка массой 8∙10-15 кг удерживается в равновесии между горизонтально расположенными обкладками плоского конденсатора. Разность потенциалов между обкладками 490 В, а зазор между ними 1 см. Определить, во сколько раз заряд пылинки больше элементарного заряда.
212. В поле бесконечной равномерно заряженной плоскости с поверхностной плотностью заряда 10 мкКл/м2 перемещается заряд из точки, находящейся на расстоянии 0,1 м от плоскости, в точку на расстоянии 0,5 м от нее. Определить заряд, если при этом совершается работа 1 мДж.
213. Какую работу нужно совершить, чтобы заряды 1 и 2 нКл, находившиеся на расстоянии 0,5 м, сблизились до 0,1 м?
214. Поверхностная плотность заряда бесконечной равномерно заряженной плоскости равна 30 нКл/м2. Определить поток вектора напряженности через поверхность сферы диаметром 15 см, рассекаемой этой плоскостью пополам.
215. Заряд 1 нКл переносится из бесконечности в точку, находящуюся на расстоянии 0,1 м от поверхности металлической сферы радиусом 0,1 м, заряженной с поверхностной плотностью 10 Кл/м2. Определить работу перемещения заряда.
216. Заряд 1 нКл притянулся к бесконечной плоскости, равномерно заряженной с поверхностной плотностью 0,2 мкКл/м2. На каком расстоянии от плоскости находился заряд, если работа сил поля по его перемещению равна 1 мкДж?
217. Какую работу совершают силы поля, если одноименные заряды 1 и 2 нКл, находившиеся на расстоянии 1 см, разошлись до расстояния 10 см?
218. Со скоростью 2∙107 м/с электрон влетает в пространство между обкладками плоского конденсатора в середине зазора в направлении параллельном обкладкам. При какой минимальной разности потенциалов на обкладках электрон не вылетит из конденсатора, если длина конденсатора 10 см, а расстояние между его обкладками 1 см?
219. Заряд -1 нКл переместился в поле заряда +1,5 нКл из точки с потенциалом 100 В в точку с потенциалом 600 В. Определить работу сил поля и расстояние между этими точками.
220. Заряд 1 нКл находится на расстоянии 0,2 м от бесконечно длинной равномерно заряженной нити. Под действием поля нити заряд перемещается на 0,1 м. Определить линейную плотность заряда нити, если работа сил поля равна 0,1 мкДж.
221. Конденсатор с парафиновым диэлектриком заряжен до разности потенциалов 150 В. Напряженность поля 6∙106 В/м, площадь пластин 6 см2. Определить емкость конденсатора и поверхностную плотность заряда на обкладках.
222. Вычислить емкость батареи, состоящей из трех конденсаторов емкостью 1 мкФ каждый при всех возможных случаях их соединения.
223. Заряд на каждом из двух последовательно соединенных конденсаторов емкостью 18 и 10 пкФ равен 0,09 нКл. Определить напряжение: а) на батарее конденсаторов; б) на каждом конденсаторе.
224. Конденсатор емкостью 6 мкФ последовательно соединен с конденсатором неизвестной емкости и они подключены к источнику постоянного напряжения 12 В. Определить емкость второго конденсатора и напряжения на каждом конденсаторе, если заряд батареи 24 мкКл.
225. Два конденсатора одинаковой емкости по 3 мкФ заряжены один до напряжения 100 В, а другой – 200 В. Определить напряжение между обкладками конденсаторов, если их соединить параллельно: а) одноименно заряженными обкладками; б) разноименно заряженными обкладками.
226. Плоский воздушный конденсатор заряжен до разности потенциалов 300 В. Площадь пластин 1 см2, напряженность поля в зазоре между ними 300 кВ/м. Определить поверхностную плотность заряда на пластинах, емкость и энергию конденсатора.
227. Найти объемную плотность энергии электрического поля, создаваемого заряженной металлической сферой радиусом 5 см на расстоянии 5 см от ее поверхности, если поверхностная плотность заряда на ней 2 мкКл/м2.
228. Площадь пластин плоского слюдяного конденсатора 1,1 см2, зазор между ними 3 мм. При разряде конденсатора выделилась энергия 1 мкДж. До какой разности потенциалов был заряжен конденсатор?
229. Энергия плоского воздушного конденсатора 0,4 нДж, разность потенциалов на обкладках 600 В, площадь пластин 1 см2. Определить расстояние между обкладками, напряженность и объемную плотность энергии поля конденсатора.
230. Под действием силы притяжения 1 мН диэлектрик между обкладками конденсатора находится под давлением 1 Па. Определить энергию и объемную плотность энергии поля конденсатора, если расстояние между его обкладками 1 мм.
231. Плотность тока в никелиновом проводнике длиной 25 м равна 1 МА/м2. Определить разность потенциалов на концах проводника.
232. Определить плотность тока, текущего по проводнику длиной 5 м, если на концах его поддерживается разность потенциалов 2 В. Удельное сопоставление материала 2 мкОм∙м.
233. Напряжение на концах проводника сопротивлением 5 Ом за 0,5 с равномерно возрастает от 0 до 20 В. Какой заряд проходит через проводник за это время?
234. Температура вольфрамовой нити электролампы 2000 °С, диаметр 0,02 мм, сила тока в ней 4 А. Определить напряженность поля нити на ее поверхности.
235. На концах никелинового проводника длиной 5 м поддерживается разность потенциалов 12 В. Определить плотность тока в проводнике, если его температура 540 °С.
236. Внутреннее сопротивление аккумулятора 1 Ом. При силе тока 2 А его к.п.д. равен 0,8. Определить электродвижущую силу аккумулятора.
237. Определить электродвижущую силу аккумуляторной батареи, ток короткого замыкания которой 10 А, если при подключении к ней резистора сопротивлением 2 Ом сила тока в цепи равна 1 А.
238. Электродвижущая сила аккумулятора автомобиля 12 В. При силе тока 3 А его к.п.д. равен 0,8. Определить внутреннее сопротивление аккумулятора.
239. К источнику тока подключают один раз резистор сопротивлением 1 Ом, другой раз – 4 Ом. В обоих случаях на резисторах за одно и то же время выделяется одинаковое количество теплоты. Определить внутреннее сопротивление источника тока.
240. Два одинаковых источника тока соединены в одном случае последовательно, в другом – параллельно и замкнуты на внешнее сопротивление 1 Ом. При каком внутреннем сопротивлении источника сила тока во внешней цепи будет в обоих случаях одинаковой?
241. Два бесконечно длинных прямолинейных проводника с токами 6 и 8 А расположены перпендикулярно друг другу. Определить индукцию и напряженность магнитного поля в середине кратчайшего расстояния между проводниками, равного 20 см.
242. По двум бесконечно длинным прямолинейным параллельным проводникам, расстояние между которыми 15 см, в одном направлении текут токи 4 и 6 А. Определить расстояние от проводника с меньшим током до геометрического места точек, в котором напряженность магнитного поля равна нулю.
243. Решить задачу 42 для случая, когда токи текут в противоположных направлениях.
244. По двум бесконечно длинным прямолинейным параллельным проводникам текут токи 5 и 10 А в одном направлении. Геометрическое место точек, в котором индукция магнитного поля равна нулю, находится на расстоянии 10 см от проводника с меньшим током. Определить расстояние между проводниками.
245. По кольцевому проводнику радиусом 10 см течет ток 4 А. Параллельно плоскости кольцевого проводника на расстоянии 2 см над его центром проходит бесконечно длинный прямолинейный проводник, по которому течет ток 2 А. Определить индукцию и напряженность магнитного поля в центре кольца. Рассмотреть все возможные случаи.
246. Два круговых витка с током лежат в одной плоскости и имеют общий центр. Радиус большого витка 12 см, меньшего – 8 см. Напряженность поля в центре витков равна 50 А/м, если токи текут в одном направлении, и нулю, если в противоположном. Определить силу токов, текущих по круговым виткам.
247. Бесконечно длинный прямолинейный проводник с током 3 А расположен на расстоянии 20 см от центра витка радиусом 10 см с током 1 А. Определить напряженность и индукцию магнитного поля в центре витка для случаев, когда проводник: а) расположен перпендикулярно плоскости витка; б) в плоскости витка.
248. По квадратной рамке со стороной 0,2 м течет ток 4 А. Определить напряженность и индукцию магнитного поля в центре рамки.
249. По квадратной рамке течет ток 4 А. Напряженность магнитного поля в центре рамки 4,5 А/м. Определить периметр рамки.
250. По квадратной рамке со стороной 0,2 м течет ток, который создает в центре рамки магнитное поле напряженностью 4,5 А/м. Определить силу тока в рамке.
251. Незакрепленный проводник массой 0,1 г и длиной 7,6 см находится в равновесии в горизонтальном магнитном поле напряженностью 10 А/м. Определить силу тока в проводнике, если он перпендикулярен линиям индукции поля.
252. Два параллельных бесконечно длинных проводника с токами 10 А взаимодействуют с силой 1 мН на 1 м их длины. На каком расстоянии находятся проводники?
253. Найти радиус траектории протона в магнитном поле с индукцией 0,5 Тл, если он движется перпендикулярно ему и обладает кинетической энергией 3 МэВ.
254. Какое ускорение приобретает проводник массой 0,1 г и длиной 8 см в однородном магнитном поле напряженностью 10 кА/м, если сила тока в нем 1 А, а направления тока и индукции взаимно перпендикулярны?
255. Электрон с энергией 300 эВ движется перпендикулярно линиям индукции однородного магнитного поля напряженностью 465 А/м. Определить силу Лоренца, скорость и радиус траектории электрона.
256. Момент импульса протона в однородном магнитном поле напряженностью 20 кА/м равен 6,6∙10 -23 кг∙м2/с. Найти кинетическую энергию протона, если он движется перпендикулярно линиям магнитной индукции поля.
257. На расстоянии 5 мм параллельно прямолинейному длинному проводнику движется электрон с кинетической энергией 1 кэВ. Какая сила будет действовать на электрон, если по проводу пустить ток 1 А?
258. Протон движется в магнитном поле напряженностью 10 А/м по окружности радиусом 2 см. Найти кинетическую энергию протона.
259. По прямолинейным длинным параллельным проводникам, находящимся на расстоянии 2 см, в одном направлении текут токи по 1 А. Какую работу на единицу длины проводников нужно совершить, чтобы раздвинуть их до расстояния 4 см?
260. Однородное магнитное поле напряженностью 900 А/м действует на помещенный в него проводник длиной 25 см с силой 1 мН. Определить силу тока в проводнике, если угол между направлениями тока и индукции магнитного поля равен 45°.
261. Перпендикулярно линиям индукции однородного магнитного поля индукцией 0,3 Тл движется проводник длиной 15 см со скоростью 10 м/с. Определить ЭДС, возникающую в проводнике.
262. Перпендикулярно линиям индукции однородного магнитного поля индукцией 0,1 мТл по двум параллельным проводникам движется без трения перемычка длиной 20 см. При замыкании цепи, содержащей эту перемычку, в ней идет ток 0,01 А. Определить скорость движения перемычки. Сопротивление цепи 0,1 Ом.
263. На концах крыльев самолета размахом 20 м, летящего со скоростью 900 км/ч, возникает электродвижущая сила индукции 0,06 В. Определить вертикальную составляющую напряженности магнитного поля Земли.
264. В плоскости, перпендикулярной однородному магнитному полю напряженностью 2∙105 А/м вращается стержень длиной 0,4 м относительно оси, проходящей через его середину. В стержне индуцируется электродвижущая сила, равная 0,2 В. Определить угловую скорость стержня.
265. Катушка из 100 витков площадью 15 см2 вращается с частотой 5 Гц в однородном магнитном поле индукцией 0,2 Тл. Ось вращения перпендикулярна оси катушки и линиям индукции поля. Определить максимальную электродвижущую силу индукции в катушке.
266. Цепь состоит из соленоида и источника тока. Соленоид без сердечника длиной 15 см и диаметром 4 см имеет плотную намотку из двух слоев медного провода диаметром 0,2 мм. По соленоиду течет ток 1 А. Определить ЭДС самоиндукции в соленоиде в тот момент времени после отключения его от источника тока, когда сила тока уменьшилась в два раза. Сопротивлением источника тока и подводящих проводов пренебречь.
267. Решить задачу 66 для случая соленоида с сердечником, магнитная проницаемость которого равна 1000.
268. Сила тока в соленоиде равномерно возрастает от 0 до 10 А за 1 мин, при этом соленоид накапливает энергию 20 Дж. Какая ЭДС индуцируется в соленоиде?
269. Однослойный соленоид без сердечника длиной 20 см и диаметром 4 см имеет плотную намотку из медного провода диаметром 0,1 мм. За 0,1 с сила тока в нем равномерно убывает с 5 А до 0. Определить электродвижущую силу индукции в соленоиде.
270. По условию задачи 69 определить заряд, прошедший через соленоид после его отключения.
271. Чему равна объемная плотность энергии магнитного поля в соленоиде без сердечника, имеющего плотную однослойную намотку проводом диаметром 0,2 мм, если по нему течет ток величины 0,1 А?
272. По условию задачи 71 найти энергию магнитного поля соленоида, если его длина 20 см, а диаметр 4 см.
273. По соленоиду длиной 0,25 м, имеющему 500 витков, течет ток 1 А. Площадь поперечного сечения 15 см2. В соленоид вставлен железный сердечник. Найти энергию магнитного поля соленоида. Зависимость B=f(H) приведена на рис 3.
274. Квадратная рамка со стороной 1 см содержит 100 витков и помещена в однородное магнитное поле напряженностью 100 А/м. Направление поля составляет угол 30° с нормалью к рамке. Какая работа совершается при повороте рамки на 30° в одну и другую сторону, если по ней течет ток 1 А?
275. По условию задачи 74 определить работу при повороте рамки в положение, при котором ее плоскость совпадает с направлением линий индукции поля.
276. Под действием однородного магнитного поля перпендикулярно линиям индукции начинает перемещаться прямолинейный проводник массой 2 г, по которому течет ток 10 А. Какой магнитный поток пересечет этот проводник к моменту времени, когда скорость его станет равна 31,6 м/с?
277. Проводник с током 1 А длиной 0,3 м равномерно вращается вокруг оси, проходящей через его конец, в плоскости перпендикулярной линиям индукции магнитного поля напряженностью 1 кА/м. За одну минуту вращения совершается работа 0,1 Дж. Определить угловую скорость вращения проводника.
278. Однородное магнитное поле, объемная плотность энергии которого 0,4 Дж/м3, действует на проводник, расположенный перпендикулярно линиям индукции, силой 0,1 мН на 1 см его длины. Определить силу тока в проводнике.
279. По обмотке соленоида с параметрами: число витков – 1000, длина 0,5 м, диаметр – 4 см; течет ток 0,5 А. Зависимость B=f(H) для сердечника приведена на рис. 3. Определить потокосцепление, энергию и объемную плотность энергии соленоида.
280. Обмотка соленоида имеет сопротивление 10 Ом. Какова его индуктивность, если при прохождении тока за 0,05 с в нем выделяется количество теплоты, эквивалентное энергии магнитного поля соленоида?
