Обобщенные характеристики сигналов и каналов связи

Первой характеристикой сигнала является его длительность Т_с.

Вторая характеристика – динамический диапазон сигнала, показывающий превышение сигнала над шумом (порогом)

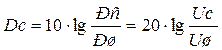. (1.45)

Например, речь (при переходе от шепота к крику) имеет динамический диапазон D_с=50 дБ.

Третьим показателем является ширина спектра сигнала

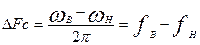, (1.46)

где 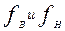- верхняя и нижняя граница спектра сигнала.

Обобщенной характеристикой сигнала является объем сигнала, определяемый выражением

V_c=T_c*D_c* 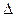F_c . (1.47)

Чтобы решить вопрос о возможности передачи сигнала по каналу связь, такие же характеристики вводятся и для канала T_к, D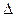_к, F_к,V_к

V_к=T_к*D_к* 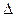F_к, (1.48)

где T_к - время использования канала,

D_к - динамический диапазон канала (способность передавать различные уровни),

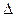F_к - ширина полосы частот, пропускаемых каналом,

V_к - емкость канала.

Передача возможна при соблюдении условий:

T_к 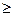T_с; D_к 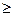D_с; F_к 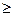F_с. (1.49)

Это требование можно ослабить, записав

V_к 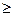V_c (1.50)

Процесс видоизменения характеристик сигнала для обеспечения возможности передачи его по заданному каналу называется согласованием сигнала с каналом связи.

Модуляция сигналов

Классификация видов модуляции

Сообщение, представленное электрическим сигналом, должно быть передано на определенное расстояние (в том числе на достаточно большое). Для этой цели используются сигналы - переносчики. Энергия переносчиков должна быть достаточной для передачи на заданное расстояние.

Таким образом, преобразование сигналов при передаче состоит в воздействии на переносчик, изменяющем тот или иной его параметр. Это воздействие называется модуляцией.

Различные виды модуляции характеризуются различными видами переносчиков, а так же рядом параметров, подвергаемых изменению.

По виду переносчиков различают:

§ модуляцию синусоидальных (гармонических) сигналов;

§ модуляцию импульсных сигналов.

По изменяемым параметрам различают:

§ амплитудную модуляцию;

§ частотную модуляцию;

§ фазовую модуляцию;

§ кодовую модуляцию и др.

В тех случаях, когда непрерывное сообщение передается в дискретной (цифровой) форме, осуществляется предварительное преобразование непрерывного сообщения в дискретное, включающее дискретизацию (квантование) по времени и по уровню.

Амплитудная модуляция

Амплитудная модуляция характеризуется изменением амплитуды A₀ переносчика 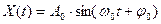по закону сигнала передаваемого сообщения

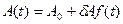, (1.51)

где 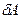- наибольшее изменение амплитуды при модуляции,

f(t) –функция, выражающая закон изменения во времени передаваемого сообщения.

Тогда амплитудно-модулированный гармонический сигнал будет иметь следующий вид

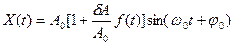, (1.52)

где 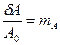- глубина амплитудной модуляции.

В том случае, когда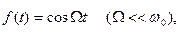

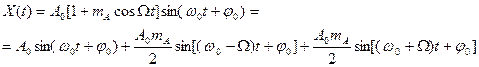(1.53)

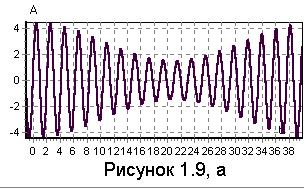Как видно из выражения (рисунок 1.9, б), спектр сигнала состоит из трех

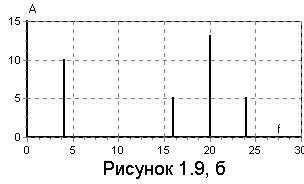
гармонических составляющих: несущей с частотой 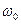и двух частот – нижней 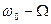и верхней - .

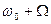Ширина спектра сигнала .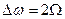

Если модуляция гармонического сигнала производится по более сложному закону, причем спектр огибающей амплитуды находится в диапазоне частот от 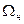(нижней) до 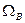(верхней), то можно показать, что в спектре амплитудно-модулированного (АМ) сигнала вместо двух боковых частот будут две боковые полосы частот : нижняя 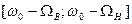и верхняя 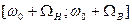. Для неискаженной передачи такого сигнала канал связи должен обладать полосой пропускания частот, равной 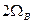, т.е. полоса пропускания должна быть в два раза больше наивысшей частоты спектра модулирующего сигнала.

Для уменьшения полосы частот модулированного сигнала, а, следовательно, и требуемой полосы пропускания канала связи применяют так называемую однополосную передачу. При такой передаче с помощью фильтров производят подавление несущей частоты и частот одной из боковых полос, т.е. передача производится в полосе частот - .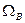

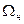При амплитудной модуляции необходимо выполнение условия 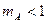. Невыполнение этого условия приводит к специфическим искажениям – так называемой перемодуляции.

Частотная модуляция

При частотной модуляции частота сигнала изменяется по закону

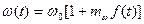, (1.54)

где 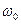- постоянная составляющая частоты;

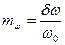- глубина частотной модуляции;

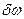- наибольшее изменение частоты при модуляции (девиация частоты);

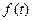- закон модуляции.

Частотно-модулированный сигнал можно представить в виде

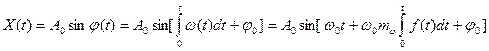, (1.55)

где 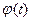- текущая фаза гармонического сигнала;

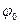- начальная фаза.

В частном случае, когда модуляция частоты осуществляется по гармоническому закону

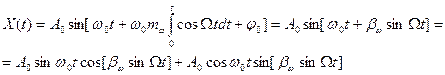, (1.56)

где 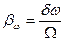- индекс частотной модуляции.

Сигнал такого вида представляется следующим образом:

,

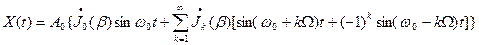где 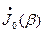- функция Бесселя нулевого порядка;

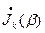- функция Бесселя k-ого порядка.

Спектр амплитуд модулированного по частоте сигнала приведен на рис. а) б). Спектр амплитуд модулированного по частоте сигнала дискретный, состоит из 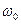и боковых частот 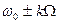. Распределение амплитуд гармонических составляющих зависит от 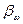- индекса частотной модуляции.

При очень маленьком 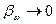спектр ЧМ не отличается от спектра АМ, т.е. содержит 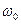, , 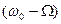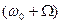. С ростом 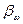увеличивается вес боковых составляющих и соответственно требуемая полоса канала связи.

Если ограничиться в спектре только составляющими, амплитуда которых составляет не менее 5-10% от 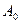до модуляции, то ширина спектра этих составляющих будет составлять .

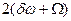При больших 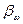( 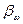>>1) ширина спектра практически равна удвоенной величине девиации частоты 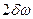и не зависит от частоты модулирующего сигнала .

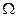Фазовая модуляция

При фазовой модуляции фаза гармонического сигнала 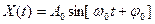изменяется по закону модулирующего сигнала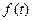

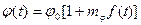, (1.57)

где 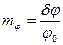- глубина фазовой модуляции ,

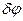- наибольшее изменение фазы при модуляции (индекс фазовой модуляции).

,

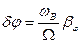где 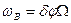- девиация частоты ФМ сигнала.

Сигнал с фазовой модуляцией можно представить в виде

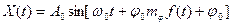. (1.58)

Так как мгновенное значение частоты является производной от фазы по времени

,

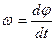то при фазовой модуляции оно может быть представлено в виде

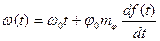. (1.59)

Таким образом, ФМ сигнал эквивалентен ЧМ сигналу с модулирующей функцией .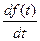

Для частотного случая, когда модулирующий сигнал является гармоническим, полная фаза ФМ сигнала определяется равенством

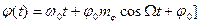, (1.60)

а ФМ колебание опишется выражением

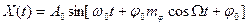. (1.61)

Мгновенное значение частоты ФМ сигнала

,

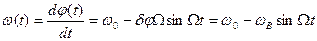где 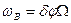- девиация частоты ФМ сигнала. Сравнение выражений (1.61) и (1.56) показывает, что при гармоническом модулирующем сигнале ЧМ и ФМ сигналы отличаются только фазой гармонической функции, определяющей изменение полной фазы в.ч. колебания. Т.е. по внешнему виду сигнала нельзя заключить, что это ЧМ или ФМ?

Однако при изменении частоты модуляции 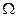проявляется различие между ЧМ и ФМ.

При ЧМ величина девиации частоты 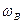зависит только от амплитуды модулирующего сигнала и не зависит от частоты модуляции 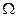. Величина же индекса 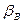убывает с ростом частоты .

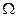При ФМ 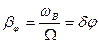, т.е. зависит только от амплитуды модулирующего сигнала и не зависит от частоты .

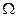В общем случае спектр ФМ сигнала с 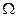, выражается также как и ЧМ сигнал с 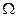(частота модуляции).

Спектр ФМ сигнала состоит из 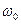и боковых частот 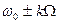. Амплитуды боковых составляющих определяются только .

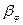При малом 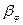спектр содержит , , .

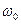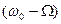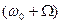При 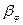>>1 практическая ширина спектра равна 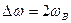, но зависит как от амплитуды, так и от частоты модулирующего сигнала, в то время как для ЧМ сигнала – зависит только от амплитуды.

Практическая ширина спектра ФМ и ЧМ сигналов примерно в 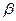раз больше, чем ширина спектра АМ сигнала при такой же частоте модуляции.