Многопозиционная модуляция

Анализ методов модуляции, рассмотренных в п.3.2, показывает, что двоичные системы передачи имеют максимальную удельную скорость передачи 2 бит/с*Гц, которую иногда называют скоростью Найквиста.

Повысить удельную скорость передачи информации можно за счет использования m -позиционной АМ или ОФМ. В этом случае один элемент линейного сигнала несет информацию о большем числе символов данных, чем в двоичных (двухпозиционных) системах.

Рассмотрим идею формирования m -позиционных методов модуляции на примере двукратной и трехкратной ОФМ с помощью амплитудно-фазовых (векторных) диаграмм.

На рис.3.16 представлены амплитудно-фазовые диаграммы дня ОФМ, ДОФМ, ТОФМ.

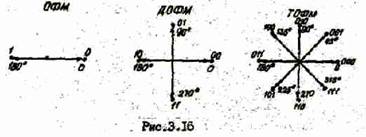
Как видно из рис.3.16, для ОФМ число значащих позиций сигнала данных m=2 со значениями фазы 0°, что соответствует символу 0, и 1800 -символу 1. При ДОФМ m=4 со значениями фаз 00, 900, 1800, 2700 и каждому вектору сигнала ставиться в соответствие два бита данных (дибита) 00, 01, 10, 11. аналогично при ТОФМ m=8 со значениями фаз 00, 450, 900, … 3150 и каждый векторсигнала соответствует трем битам данных (трибитам) 000, 001, … 111.

Число двоичных символов данных k, равное кратности фаз, из-за удобства реализации должно быть целым. Для ОФМ k=1, для ДОФМ k=2 и для ТОФМ k=3. С числом значащих позиций сигнала данных m оно связано соотношением .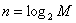

Коды Хемминга.

Код Хэмминга, являющийся групповым (n,k) кодом, с минимальным расстоянием d=3 позволяет обнаруживать и исправлять однократные ошибки. Для построения кода Хэмминга используется матрица H. 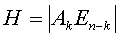, где A_k- транспонированная подматрица, E_n-k - единичная подматрица порядка n-k.

Если Х - исходная последовательность, то произведение Х·Н=0. Пусть E- вектор ошибок. Тогда (Х+Е)·Н = Х·Н+Е·Н = 0+Е·Н=E·H - синдром или корректор, который позволяет обнаружить и исправить ошибки. Контрольные символы e₁ ,e₂ ,...,e_r образуются из информационных символов, путем линейной комбинации 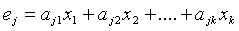, где а_j={0,1} - коэффициенты, взятые из подматрицы A матрицы H.

Рассмотрим Построение кода Хэмминга для k=4 символам. Число контрольных символов r=n-k можно определить по неравенству Хэмминга 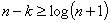для однократной ошибки. Но так, как нам известно, только исходное число символов k, то проще вычислить по эмпирической формуле

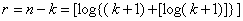, (5.2)

где [.] - означает округление до большего ближайшего целого значения. Вычислим для k=4 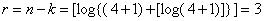. Получим код (n,k)=(7,4); n=7; k=4; r=n-k=3; d=3. Построим матрицу H.

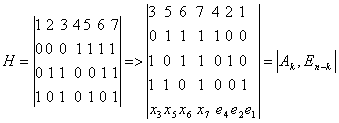
Контрольные символы e_j определим по формуле .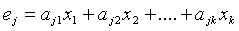

Общие сведения о цифровой передаче непрерывных сообщений. Постановка задачи об оптимальном демодуляторе (приемнике) дискретных сообщений. Оптимальный прием в дискретно-непрерывном канале без искажений при наличии аддитивного белого шума.

Для передачи непрерывных сигналов можно использовать дискретный канал, преобразуя непрерывный сигнал в цифровой с помощью АЦП, а на приемной стороне цифровой сигнал в непрерывный с помощью ЦАП.

Применение цифровых систем передачи (ЦСП) дает возможность объединения различных видов связи на единой цифровой основе, а также широко использовать современную элементную базу, обеспечивая стабильность характеристик, надежность, и хорошие массо-габаритные показатели.

Принцип АЦП на основе импульсно-кодовой модуляции (ИКМ) включает дискретизация во времени, квантование по уровню (амплитуде) и кодирование [5, 6, 18, 20, 21].

Процесс формирования ИКМ сигнала поясним с помощью упрощенной структурной схемы (рис.6.8) и временных диаграмм (рис. 6.9).

Дискретизация заключается в том, что непрерывный сигнал 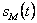(рис. 6.9,а) заменяется отсчетами 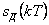(на рис. 6.9,б), следующими через одинаковые интервалы времени 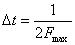. Например, для речевого сигнала, где 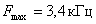, принят стандартный интервал , .

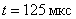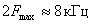Процесс дискретизации эквивалентен импульсной модуляции. Для примера на рис. 6.9,б приведен случай АИМ.

Различают равномерное и неравномерное квантование. При квантовании устанавливается количество уровней 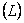разрешенных для передачи.

Процесс квантования состоит в следующем текущие значения сигнала соответствующее моменту отсчета 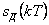заменяется ближайшим дискретным значением 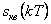(уровнем), такая операция подобна округлению и приводит к ошибке:

,

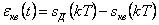Модель Гильберта.

модели каналов не способны описать пульсирующую природу реальных каналов передачи. Поэтому Гильбертом была предложена следующая модель канала с ошибками. Вероятность ошибки в текущем состоянии сети зависит от того, в каком состоянии находилась сеть в предыдущий момент времени. То есть подразумевается, что имеет место корреляция между двумя последовательными событиями. Таким образом, проявляется память канала и его пульсирующая природа. Модель Гильберта по сути является моделью Маркова первого порядка с двумя состояниями – «хорошим» и «плохим». Если ошибки в принятых данных отсутствуют, то речь идет о «хорошем» состоянии. В «плохом» состоянии вероятность ошибки принимает некоторое значение большее, чем 0. На рис. 4 показана модель Гильберта.

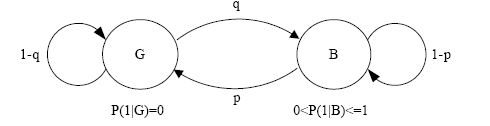
Рис. 4. Схематическая иллюстрация модели Гильберта

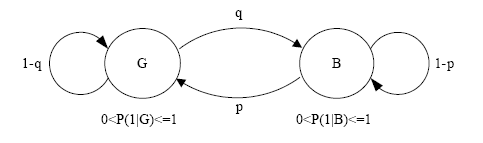
Рис. 5. Схематическая иллюстрация модели Гильберта-Эллиота

Вероятность того, что канал находится в «плохом» состоянии равна

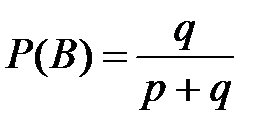
и таким образом, полная вероятность ошибки

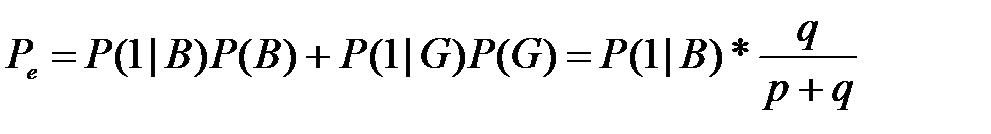
Модель Гильберта является самовозобновляемой моделью, это означает, что длины пачек ошибок и длины безошибочных промежутков не зависят от предшествующих пачек и промежутков ошибок.