Теплоемкость идеального газа.Теплоемкость при постоянном объеме и давлении. Уравнение Майера.
Работа и теплота.
Теплота - кинетическая часть внутренней энергии вещества, определяемая интенсивным хаотическим движением молекул и атомов, из которых это вещество состоит.Мерой интенсивности движения молекул является температура.Количество теплоты, которым обладает тело при данной температуре, зависит от его массы; например, при одной и той же температуре в большой чашке с водой заключается больше теплоты, чем в маленькой, а в ведре с холодной водой его может быть больше, чем в чашке с горячей водой (хотя температура воды в ведре и ниже).Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины и направления силы (сил) и от перемещения точки (точек) тела или системы
 Q-A+ΔU ΔU=Q-A
Q-A+ΔU ΔU=Q-A
Количество тепла, сообщаемое системе расходуется на соверш. Работы, а остаток идет на увеличение.
Теплоемкость при V. Удельной теплоемкостью будем называть V=1/m=ΔQ/ΔT
C-молярная теплоемкость =кол-во тепла для 1 моля вещ-ва, чтобы t увеличилась на 1 градус.
C= ϻ/m= ΔQ/ΔT
Теплоемкость идеального газа.Теплоемкость при постоянном объеме и давлении. Уравнение Майера.
Если в результате теплообмена телу передается некоторое количество теплоты, то внутренняя энергия тела и его температура изменяются. Количество теплоты Q, необходимое для нагревания 1 кг вещества на 1 К называют удельной теплоемкостью вещества c. c = Q / (mΔT).
Во многих случаях удобно использовать молярную теплоемкость C: C = M · c,
где M – молярная масса вещества. Определенная таким образом теплоемкость не является однозначной характеристикой вещества. Согласно первому закону термодинамики изменение внутренней энергии тела зависит не только от полученного количества теплоты, но и от работы, совершенной телом.
В зависимости от условий, при которых осуществлялся процесс теплопередачи, тело могло совершать различную работу. Поэтому одинаковое количество теплоты, переданное телу, могло вызвать различные изменения его внутренней энергии и, следовательно, температуры. Такая неоднозначность определения теплоемкости характерна только для газообразного вещества.
При нагревании жидких и твердых тел их объем практически не изменяется, и работа расширения оказывается равной нулю. Поэтому все количество теплоты, полученное телом, идет на изменение его внутренней энергии. В отличие от жидкостей и твердых тел, газ в процессе теплопередачи может сильно изменять свой объем и совершать работу. Поэтому теплоемкость газообразного вещества зависит от характера термодинамического процесса. Обычно рассматриваются два значения теплоемкости газов: CV – молярная теплоемкость в изохорном процессе (V = const) В процессе при постоянном объеме газ работы не совершает: A = 0. Из первого закона термодинамики для 1 моля газа следует QV = CVΔT = ΔU. Изменение ΔU внутренней энергии газа прямо пропорционально изменению ΔT его температуры. Cp – молярная теплоемкость в изобарном процессе (p = const). Для процесса при постоянном давлении первый закон термодинамики дает: Qp = ΔU + p(V2 – V1) = CVΔT + pΔV,
где ΔV – изменение объема 1 моля идеального газа при изменении его температуры на ΔT.
Отсюда следует: CP=QP/ ΔT=CV+P(ΔV/ΔT)Отношение ΔV / ΔT может быть найдено из уравнения состояния идеального газа, записанного для 1 моля: pV = RT,где R – универсальная газовая постоянная. При p = const: PΔV=RΔTилиΔV/ΔT = R/P .Таким образом, соотношение, выражающее связь между молярными теплоемкостями Cp и CV, имеет вид (формула Майера): Cp = CV + R. Теплоемкость идеального газаОстановимся подробнее на теплоемкости идеального газа. Будем рассматривать молярную теплоемкость C=dQ/vdT. Величина теплоемкости зависит от условий, при которых происходит нагревание газа. Наибольший интерес представляет теплоемкость для случаев, когда нагревание происходит при постоянном объеме или постоянном давлении. Для первого случая теплоемкость обозначается Cv и равна Cv=(i/2)R, для второго случая теплоемкость обозначается Cp и равна Cp=((i+2)/2)R, где i – число степеней свободы молекулы. Для изотермического процесса теплоемкость CТ = ¥, а для адиабатического процесса теплоемкость Cадиаб. = 0.
Согласно рассмотренной нами теории теплоемкости Cv и Cp газов должны быть целыми, кратными R/2, ибо число степеней свободы может быть только целым. Поэтому даже малые расхождения между теоретическими и экспериментальными значениями Cv и Cp играют принципиальную роль. Такое расхождение можно обнаружить, если обратится к температурной зависимости теплоемкости газа. На рисунке изображена кривая зависимости молярной теплоемкости Cv от температуры Т, полученная опытным путем для водорода. Согласно теории теплоемкость не должна зависеть от температуры. Из рисунка видно, что это оказывается справедливым только в пределах отдельных температурных интервалов, причем в различных интервалах теплоемкость имеет значения, соответствующие различному числу степеней свободы молекулы. Так, на участке 1 – 1’ Cv равно 3/2 R. Это означает, что молекула ведет себя, как система, обладающая только поступательными степенями свободы. На участке 2 – 2’ Cv равно 5/2 R. Следовательно, при температурах, соответствующих этому участку, у молекулы, в дополнение к проявившимся при более низких температурах трем поступательным степеням свободы, добавляются еще две вращательные. Наконец, при достаточно больших температурах (Т > 1000 К) теплоемкость Cv делается равной 7/2 R , что свидетельствует о наличии при этих температурах колебаний молекулы. В промежутках между указанными интервалами теплоемкость монотонно растет с температурой.
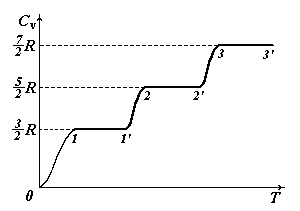 Рис. 9 Рис. 9 |
Объяснение такого поведения теплоемкости дается квантовой механикой. Как устанавливает квантовая теория, энергия вращательного и колебательного движений молекул оказывается квантованной. Это означает, что энергия вращения и энергия колебания молекулы могут иметь не любые значения, а только дискретные (т.е. отдельные, отличающиеся друг от друга на конечную величину) значения. Следовательно, энергия, связанная с этими видами движения, может меняться только скачками. Для энергии поступательного движения такого ограничения не существует.
Интервалы между уровнями энергии для колебания примерно в десять раз больше, чем для вращения. Этим и объясняется тот факт, что при низких температурах молекулы участвуют только в поступательном движении, и Cv = 3/2 R. При повышении температуры наступает такой момент, когда молекулы вовлекаются во вращательное движение, и Cv = 5/2 R. Наконец, при дальнейшем повышении температуры (Т > 1000 К) молекулы будут участвовать также и в колебательном движении, и Cv = 7/2 R. Участки кривой 1’– 2 , 2’ – 3 означают, что не все молекулы сразу вовлекаются во вращательное (участок 1’– 2) движение, а также в колебательное (участок 2’– 3) движение.
Таким образом, классическая теория теплоемкости приблизительно верна лишь для отдельных температурных интервалов, причем каждому интервалу соответствует свое число степеней свободы молекулы.
При сообщении телу некоторого количества теплоты изменяется его температура (за исключением агрегатных превращений и вообще изотермических процессов). Характеристиками такого изменения являются различные теплоемкости: теплоемкость тела CT, удельная теплоемкость вещества c, молярная теплоемкость C.
Понятия теплоемкости тела и удельной теплоемкости рассмотрены тут.
Молярная теплоемкость C — величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К: C=Q/(vΔT)
Единицей молярной теплоемкости в СИ является джоуль на моль-Кельвин (Дж/моль·К).
Удельная теплоемкость связана с молярной соотношением C=cM
В отличие от такой, например, характеристики вещества, как его молекулярная масса Mr удельная теплоемкость вещества не является неизменным параметром. Удельная теплоемкость может резко изменяться при переходе вещества из одного агрегатного состояния в другое. Так, вода в газообразном состоянии имеет удельную теплоемкость 2,2·103 Дж/кг·К а в жидком 4,19·103 Дж/кг·К .
Теплоемкость зависит и от условий, при которых происходит передача теплоты телу. Последнее особенно относится к газам. Например, при изотермическом расширении газа ему передается некоторое количество теплоты Q > 0, а ΔΤ = 0. Следовательно, удельная теплоемкость газа при изотермическом процессе C=Q/(mΔT)->бесконечность
При адиабатном сжатии (расширении) газ не получает теплоты и не передает ее окружающим телам (Q = 0), а температура газа изменяется (ΔΤ ≠ 0). Следовательно, удельная теплоемкость газа при адиабатном процессе c=Q/(mΔT)=0 . Наибольший интерес представляет теплоемкость для случаев, когда нагревание происходит при постоянном объеме или при постоянном давлении. В первом случае теплоемкость называется теплоемкостью при постоянном объеме или изохорной теплоемкостью (cV, CV), во втором — теплоемкостью при постоянном давлении или изобарной теплоемкостью (cp, Cp).
