Геометрична оптика

· Закон відбивання світла:

падаючий, відбитий промені та перпендикуляр, поставлений в точці падіння променя до межі розділу двох середовищ, лежать в одній площині; кут відбивання світлового променя дорівнює куту падіння.

· Для сферичного дзеркала з радіусом кривини поверхні R пучок паралельних променів після відбивання сходяться у фокусі F на відстані від дзеркала:

.

Для вгнутого сферичного дзеркала фокус F є дійсним, а для опуклого – уявним. Тому величина F додатна для вгнутого і від’ємна для опуклого дзеркал.

· Формула дзеркала:

.

де d – відстань від дзеркала до предмета; f – відстань від дзеркала до зображення. У формулі дзеркала знак біля f: для дійсного зображення є “+”, а для уявного – “-“.

· Поперечне (лінійне) збільшення m зображення дзеркала :

,

де h – висота предмета; Н – висота зображення. Якщо m позитивне, то зображення пряме; якщо ж негативне, то зображення перевернуте. Опукле дзеркало завжди дає уявне, пряме і зменшене зображення предмета.

· Закон заломлення світла:

падаючий, заломлений промені та перпендикуляр, поставлений в точці падіння променя до межі розділу двох середовищ, лежать в одній площині; відношення синуса кута α₁ падіння до синуса кута α₂ заломлення є величина стала для даної пари середовищ, визначається відношенням швидкості υ₁ поширення світла в першому середовищі до швидкості υ₂ поширення світла в другому середовищі і називається відносним показником заломлення другого середовища відносно першого:

.

де n₁та n₂ – абсолютні показники заломлення середовищ.

· Абсолютний показник заломлення n середовища:

,

де с – швидкість світла у вакуумі; υ – швидкість світла у середовищі.

· Закон Снелліуса:

.

· Граничний кут падіння α_гр:

.

· Для тонкої лінзи з показником заломлення n_л, яка міститься в середовищі з показником заломлення n_с, оптична сила D лінзи становить:

,

де R₁та R₂ – радіуси кривини поверхонь лінзи, які враховують знак (“+” чи “-”) залежно від форми поверхні (опукла чи вгнута) по відношенню до падаючого променя.

· Формула тонкої лінзи:

,

де d – відстань від лінзи до предмета, а f – відстань від лінзи до зображення.

Усі відстані відраховуються вздовж головної оптичної осі лінзи. Відстань від лінзи до предмета d береться із знаком “+”. Відстань f до зображення предмета, яка відраховуються від лінзи за ходом променя, вважаються додатною, а проти ходу про­меня - від'ємною. Знак біля відстаніf визначається отриманим зображенням: для дійсного зображення він є “+”, а для уявного – “-”. Своєю чергою, фокусна відстань (як і оптична сила) збиральної лінзи береться із знаком “+”, а розсіювальної лінзи – із знаком “-”.

· Оптична сила двох тонких лінз (системи лінз), які складені разом:

.

· Поперечне (лінійне) збільшення kзображення лінзою визначається за формулою:

,

де h – висота предмета, а Н – висота зображення.

· Кут відхилення світлових променів призмою:

,

де 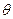– заломлюючий кут призми; 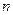– показник заломлення речовини, з якої виготовлена призма.

12.1. Два плоскі дзеркала дотикаються так, що утворюють між собою кут 120⁰. На перше дзеркало падає світловий промінь під кутом падіння 50⁰ і, відбившись, попадає на друге дзеркало. Яким буде кут відбивання променя від другого дзеркала ?

12.2. У кімнаті довжиною L = 5 м і висотою Н = 3 м висить на стіні плоске дзеркало. Людина дивиться в нього, знаходячись на віддалі l = 1 м від тієї стіни, на якій воно висить. Яка повинна бути найменша висота дзеркала, щоб людина могла бачити стіну, котра знаходиться за її спиною, у всю висоту ?

12.3. Плоске дзеркало обертається з постійною частотою ν = 0,5 с^-1. З якою лінійною швидкістю буде переміщатись “зайчик” по сферичному екрані радіусом 10 м, якщо дзеркало знаходиться у центрі кривизни екрана?

12.4. Предмет висотою 1,2 см розміщений на відстані 2 см від вгнутого дзеркала з радіусом кривини 8 см. Знайти відстань від дзеркала до зображення предмета та висоту зображення.

12.5. Предмет висотою 1,2 см розміщений на відстані 2 см від опуклого дзеркала з радіусом кривини 8 см. Знайти відстань від дзеркала до зображення предмета та висоту зображення.

12.6. Предмет знаходиться на відстані 15 см від вгнутого сферичного дзеркала з радіусом кривини 20 см. Побудувати зображення предмета та визначити його лінійне збільшення.

12.7. Предмет знаходиться на відстані 15 см від опуклого сферичного дзеркала з радіусом кривини 20 см. Побудувати зображення предмета та визначити його лінійне збільшення.

12.8. Тонкий непрозорий диск радіусом 10 см міститься на відстані 80 см від екрана. На відстані 100 см від екрана перед диском розміщене точкове джерело світла. Чому дорівнює радіус круглої тіні на екрані?

12.9. Тонкий непрозорий диск радіусом 10 см міститься на відстані 80 см від екрана. На відстані 100 см від екрана перед диском розміщене джерело світла, яке також має форму тонкого диска радіусом 5 см. Чому дорівнюють радіуси тіні і півтіні, які утворюються при цьому на екрані? Площини дисків паралельні між собою та площиною екрану, центри дисків лежать на одному перпендикулярі до площини екрану.

12.10. Промінь світла падає у воді на скляну пластинку. Показник заломлення води n₁ = 1,33; показник заломлення скла n₂ = 1,5. Яким повинен бути кут падіння променя, щоб відбитий від межі розділу промінь був перпендикулярний до заломленого ?

12.11. Визначити, наскільки плоскопаралельна скляна пластинка товщиною d = 10 см зміщує в сторону промінь світла, який падає з повітря на неї під кутом α₁ = 70⁰. Показник заломлення скла n = 1,5.

12.12. Промінь світла потрапляє з повітря під кутом падіння 30° на плоскопаралельну пластинку і виходить з неї паралельно до початкового променя. Показник заломлення скла 1,5. Яка товщина d пластинки, якщо бокове зміщення променя складає 1,94 см ?

12.13. Вертикально розміщений в озері стовп виступає з вода на 1,2 м. Визначити довжину тіні на дні озера, якщо промені Сонця падають на поверхню води під кутом 45°, а глибина озера 1 м. Показник заломлення води дорівнює 1,33.

12.14. Показник заломлення товстої прозорої пластинки змінюється від n₁ = 1,4 на верхній грані, до n₂ = 1,5 на нижній. Верхня грань пластинки межує із середовищем з показником за­ломлення n₀ = 1,33, а нижня – із середовищем з показником заломлення n₃= 1,7. Промінь світла потрапляє на верхню грань пластинки під кутом падіння α₁ = 30⁰. Під яким кутом промінь вийде з товстої пластинки?

12.І5. Людина, яка стоїть на березі озера, дивиться на камінь, що лежить на його дні. Глибина озера h = 1 м. На якій віддалі від поверхні води буде зображення каменя, якщо кут зору складає з нормаллю до поверхні води кут 60°? Показник заломлення води n = 1,33.

I2.I6. Яким повинен бути зовнішній радіус згину світловоду, зробленого з прозорої речовини з показником заломлення n = 4/3, щоб при діаметрі світловоду d = 1 мм світло, яке увійшло в світловод перпендикулярно до площини перерізу, поши­рювалось, не виходячи назовні через бічну поверхню?

12.17. Переріз скляної призми має форму рівностороннього трикутника. Промінь світла падає перпендикулярно на одну із його граней. Знайти кут φ між падаючим променем і променем, який вийшов з призми. Показник заломлення скла n = 1,5.

12.18. Промінь, який падає на одну із граней призми, виходить після заломлення через суміжну грань. Яке максимально допустиме значення заломлюючого кута θ призми, якщо вона зроблена із скла з показником заломлення n = 1,5 ?

12.19. Знайти фокусну віддаль лінзи, яка занурена у воду, якщо відомо, що її фокусна віддаль в повітрі дорівнює 20 см. Показник заломлення матеріалу лінзи n_л = 1,6. Показник заломлення води n_в = 1,33.

12.20. Симетрична двоопукла тонка лінза, показник заломлення якої n_л = 1,45, занурена в рідину, показник заломлення якої дорівнює n_р = 1,6. Радіуси кривини поверхонь лінзи однакові і дорівнюють R₁ = R₂= 16 см. Яке буде збільшення зображен­ня предмета, котрий міститься в рідині на відстані 150 см від лінзи?

12.21. Дві однакові за розмірами опуклі лінзи виготовлені зі скла з показником заломлення n₁ = 1,5 тa n₂ = 1,7. Знайти відношення їх фокусних відстаней. Що буде з променем, який іде паралельно до оптичної осі, якщо лінзи занурити в прозору рідину з показником заломлення n_р = 1,6 ?

12.22. Відстань від предмета до екрана L = 50 см. Збірна лінза, вміщена між ними, дає чітке зображення предмета на екрані у двох положеннях. Відстань між цими положеннями l = 10 cм. Якими будуть збільшення зображення предмета у цих двох положеннях лінзи?

12.23. Радіуси кривини поверхонь опуклої лінзи однакові і дорівнюють R₁ = R₂= 50 см. Показник заломлення матеріалу лінзи n_л = 1,5. Знайти оптичну силу лінзи.

12.24. На віддалі 15 см від опуклої лінзи з оптичною силою 10 діоптрій, знаходиться предмет висотою 2 см. Знайти положення і висоту зображення предмета. Зробити рисунок.

12.25. Лінза з фокусною віддаллю 16 см дає чітке зображення предмета при двох положеннях, віддаль між якими 60 см. Знайти віддаль від предмета до екрана.

12.26. Висота полум’я свічки 5 см. Лінза дає на екрані зображення цього полум’я висотою 15 см. Не рухаючи лінзи, свічку відсунули на L = 1,5 см далі від лінзи і, пересунувши екран, знову отримали чітке зображення полум'я висотою 10 см. Визначити фокусну відстань лінзи.

12.27. Дві тонкі лінзи в фокусними відстанями F₁ = 20 см та F₂ = 25 см знаходяться на віддалі L = 5 см одна від одної, утворивши центровану систему. Знайти фокусну відстань цієї системи.

12.28. Знайти фокусну відстань F центрованої системи, яка склада­ється з двох тонких лінз з фокусними відстанями F₁ = 20 см та F₂ = 25 см, які знаходять­ся на відстані L = 5 см одна від одної, якщо простір між ними заповнено водою. Показник заломлення води n_в = 1,33.