Закон ома для цепей переменного тока

Цель: экспериментально определить импеданс различных нагрузок и сопоставить экспериментальные значения с теоретическими.

Теоретическая часть

Рассмотрим соотношения между током и напряжением в цепи переменного тока при включении в нее различных нагрузок (рис. 29).

Омическое сопротивление. Под этим термином понимают сопротивление проводника постоянному току. В дальнейшем будем рассматривать квазистационарные токи, для которых мгновенные значения силы тока и напряжения, обозначаемые малыми буквами i и u, подчиняются законам Ома и Джоуля-Ленца. Амплитудные значения тока и напряжения будем обозначать I_m и U_m.

Пусть к омическому сопротивлению приложено напряжение, меняющееся по гармоническому закону:

U = U_mсos wt, (31)

где w – циклическая частота колебаний. Согласно закону Ома через R потечет ток силой i:

(32)

или

i = I_mсos wt, (33)

Из соотношений (32) и (33) следует:

1) фазы тока и напряжения на омическом сопротивлении совпадают;

2) амплитуды силы тока и напряжения связаны соотношением

. (34)

Рис. 29. Омическая, индуктивная и емкостная нагрузки

Индуктивное сопротивление. Подадим на катушку, обладающую индуктивностью L и пренебрежимо малым омическим сопротивлением, напряжение, меняющееся по закону (31). В катушке возникает меняющийся ток, создающий переменное магнитное поле. Изменение магнитного потока Ф = Li этого поля возбудит в витках катушки ЭДС самоиндукции

.

Поскольку подводимое к катушке напряжение играет роль ЭДС, а падение напряжения в цепи отсутствует (R = 0), по второму правилу Кирхгофа для мгновенных значений можем записать:

u + = 0 или .

Последнее перепишем в виде дифференциального уравнения

или .

Интегрирование этого уравнения дает следующее выражение:

.

Так как

,

то

(35)

Из (31) и (35) следует:

1) ток, проходящий через катушку, отстает от напряжения по фазе на p/2 или, что то же самое, напряжение опережает ток по фазе на p/2;

2) амплитуды тока и напряжения связаны соотношением

. (36)

Из сопоставления (36) с (32) следует, что величина wL в цепи с индуктивностью играет роль сопротивления. Величину

X_L = wL (37)

называют индуктивным сопротивлением.

Емкостное сопротивление. Конденсатор представляет собой разрыв проводов, поэтому постоянный ток он не пропускает. При изменении напряжения между обкладками меняется и мгновенное значение заряда конденсатора, определяемого формулой

q = Cu, (38)

для чего в подводящих проводах должен протекать ток, приносящий заряд к обкладкам или уносящий от них. Говорят, что конденсатор пропускает переменный ток, хотя в пространстве между обкладками никакой передачи заряда от одной обкладки к другой не происходит.

Проходящий по проводам заряд скапливается на обкладках конденсатора, поэтому его величина равна i = dq/dt, где q – мгновенное значение заряда обкладки. Учитывая (38) и считая подаваемое напряжение меняющимся по закону (31), получаем:

.

Так как cos (p/2 + wt) = –sin wt, последнее примет вид:

. (39)

Сопоставляя (31) и (39), имеем:

1) ток в цепи с конденсатором опережает напряжение по фазе на p/2, иначе говоря, напряжение отстает от тока по фазе на p/2;

2) амплитуды тока и напряжения связаны соотношением

. (40)

Величину

(41)

называют емкостным сопротивлением.

При измерениях и расчетах цепей переменного тока вместо амплитудных пользуются действующими (эффективными) значениями силы тока I и напряжения U, которые связаны с амплитудными:

, .

Их использование обусловлено тем, что закон Джоуля-Ленца в случае переменного тока принимает такой же вид, как и для постоянного. Соответственно электроизмерительные приборы градуируются на эффективные значения.

Очевидно, что формулы (34), (36) и (40) не изменяются при замене амплитудных значений на эффективные и примут вид:

U_R = I × R, U_L = I × wL, U_C = I/wC, (42)

где индексы R, L и C означают напряжение на соответствующей нагрузке.

Векторные диаграммы. Фазовые соотношения между током и напряжением графически изображены на рис. 30.

Рис. 30

Существует и другой способ их представления, позволяющий упростить расчеты цепей со сложной нагрузкой.

Рис. 31

Проведем из некоторой точки О (рис. 31) ось ОХ и отложим из той же точки вектор А под углом j к оси ОХ. Затем приведем этот вектор во вращение вокруг точки О в плоскости рисунка против часовой стрелки с угловой скоростью w. Угол a между А®и ОХ спустя время t будет a = wt + j. Проекция А® на ось ОХ равна

А_Х = Х = Acos a

или

Х = Acos (wt + j). (43)

Вывод: всякое гармоническое колебание можно представить вращением вектора соответствующей длины и ориентации.

Следовательно, если построить вектор U и под соответствующим углом отложить вектор I, то при совместном вращении векторов угол между ними останется неизменным (43). Векторные диаграммы токов и напряжений при различных нагрузках приведены на рис. 32.

Рис. 32

Последовательное соединение R, L и С. Для расчета такой цепи воспользуемся методом векторных диаграмм. При последовательном соединении нагрузок мгновенное значение силы тока во всех точках цепи должно быть одинаковым, т.е. фаза тока на всех нагрузках одинакова.

Однако напряжения на нагрузках не совпадают по фазе с током. Напряжение на омическом сопротивлении совпадает по фазе с током, на индуктивном – опережает ток на p/2, на емкостном – отстает на p/2. Таким образом, сложив векторы U_R, U_L и U_C, получим полное напряжение, приложенное к цепи. Поскольку U_L и U_C противоположны по направлению, удобнее сначала сложить их, а затем вектор U_L – U_C сложить с U_R. В итоге имеем:

.

Подставляя соотношения (42), получим:

. (44)

В этом выражении роль сопротивления выполняет величина

, (45)

называемая полным сопротивлением цепи переменному току или импедансом. С ее использованием (44) примет вид:

U = I × Z. (46)

Это выражение часто называют законом Ома для переменных токов. Величина

(47)

называется реактивным сопротивлением и является комбинацией индуктивного и емкостного сопротивлений.

Векторная диаграмма (рис. 33) также показывает, что приложенное напряжение и протекающий в цепи ток колеблются не в одинаковой фазе, а имеют между собой сдвиг фаз j, величина которого определяется любой из приведенных ниже формул, следующих из диаграммы:

; ;

(48)

.

Рис. 33. Смешанная нагрузка и векторная диаграмма для нее

Следует отметить, что формула (46) является общей для любого соединения нагрузок, а формулы (45), (47) и (48) справедливы лишь для частного случая последовательного соединения.

Экспериментальная часть

Оборудование: реостат 1000 Ом, ключ, амперметр, вольтметр, реостат 100 Ом, батарея конденсаторов, катушка.

Порядок выполнения работы

Рис. 34. Рабочая схема и используемые нагрузки

Задание 1. Измерение омического сопротивления.

Схема установки приведена на рис. 34.

В этом опыте в качестве нагрузки применяется низкоомный реостат. Высокоомный реостат используется как потенциометр.

1. Измерить ток через нагрузку при трех различных значениях подаваемого на нее напряжения. Результаты измерения занести в табл. 12.

Задание 2. Измерение емкостного сопротивления.

1. В рабочую схему в качестве нагрузки включить батарею конденсаторов. Ток и напряжение на нагрузке измерить аналогично заданию 1. Результаты измерения также внести в табл. 12.

Примечание. Значение емкости батареи рекомендуется выбрать в интервале 20–40 мкФ.

Задание 3. Измерение импеданса катушки.

1. Измерение импеданса катушки проводится аналогично предыдущим заданиям с использованием катушки в качестве нагрузки.

Задание 4. Измерение импеданса последовательного соединения R, L и С.

1. Нагрузкой будут служить соединенные последовательно реостат, батарея конденсаторов и катушка.

2. Ток и напряжение на нагрузке измерить аналогично заданию 1.

3. По результатам каждого измерения вычислить импедансы Z_эксп нагрузок.

4. Сравнить экспериментальные результаты с теоретическими или паспортными значениями. Результаты сравнения привести в выводе.

Таблица 12

Номер задания	Напряжение, U	Сила тока, I	Zэксп, Ом	Zэкспср, Ом	Zтеор, Ом
цена деления	в делениях	в В	цена деления	в делениях	в А
резистор
конденсатор
катушка
4 последовательное соединение

Примечание. Теоретическим для реостата будет его паспортное значение сопротивления. Для конденсатора Z_теор определяется по использованному в опыте значению емкости, расчет производится по формуле (41). Катушка обладает и омическим, и индуктивным сопротивлением, поэтому ее импеданс вычисляется по формуле (45), причем в качестве R должна использоваться сумма омических сопротивлений реостата и катушки.

5. Вычисление погрешностей экспериментальных значений произвести по классам точности амперметра и вольтметра, теоретических – по паспортным данным приборов.

Контрольные вопросы и задания

1. Запишите и поясните закон Ома для переменного тока.

2. Как определяется омическое, реактивное и полное сопротивление в цепи переменного тока?

3. Что понимается под эффективными значениями тока и напряжения?

4. Нарисуйте векторную диаграмму для резистора в цепи переменного тока. Сделайте пояснения.

5. Нарисуйте векторную диаграмму для конденсатора в цепи переменного тока. Сделайте пояснения.

6. Нарисуйте векторные диаграммы для идеальной катушки и катушки с заметным омическим сопротивлением в цепи переменного тока. Сделайте пояснения.

7. Нарисуйте векторную диаграмму для последовательного соединения резистора, конденсатора и катушки в цепи переменного тока. Сделайте пояснения. Получите из векторной диаграммы закон Ома.

Лабораторная работа 9 (11)

ИЗМЕРЕНИЕ МОЩНОСТИ

В ЦЕПИ ПЕРЕМЕННОГО ТОКА

Цель: ознакомиться с измерением мощности в цепи переменного тока методом трех вольтметров.

Теоретическая часть

Как всякий проводник, катушка в цепи постоянного тока потребляет энергию, идущую на нагревание проводов. Свойство проводника превращать энергию электрического тока в тепловую характеризуется его омическим сопротивлением R. Мощность тепловых потерь определяется по формуле

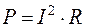, (49)

где I – сила тока в проводнике.

При включении катушки в цепь переменного тока у нее также происходит выделение тепла по закону (49), но в этом случае I – эффективное значение силы переменного тока.

Если у катушки имеется ферромагнитный сердечник, то проходящий по катушке переменный ток возбуждает в нем вихревые токи (токи Фуко), ведущие к нагреванию сердечника. Кроме того, происходит непрерывное изменение намагниченности сердечника по величине и направлению (перемагничивание), что также приводит к нагреванию сердечника. Эти дополнительные потери энергии эквивалентны возрастанию сопротивления проводника. Совокупные необратимые потери энергии, идущие на нагревание как проводов, так и сердечника, характеризуются активным сопротивлением катушки, определяемым по формуле

. (50)

Это сопротивление, в отличие от омического, невозможно измерить, его можно лишь рассчитать.

Падение напряжения на активном сопротивлении считается колеблющимся в фазе с током.

Рис. 35

При отсутствии ваттметра мощность, потребляемая катушкой, может быть определена с использованием трех вольтметров. Если катушка обладает индуктивностью L и активным сопротивлением R_а, то между током в катушке и напряжением на ней возникает сдвиг фаз j, что иллюстрируется векторной диаграммой (рис. 35), где I – ток через катушку, U_а и U_L – падения напряжения на активном и индуктивном сопротивлениях катушки, U_к – полное напряжение на катушке.

Потребляемую катушкой мощность можно вычислить либо из (49), либо по формуле

. (51)

I и U_к измеряют непосредственно, а для определения коэффициента мощности (сos j) последовательно с катушкой включается омическое сопротивление R.

Из векторной диаграммы (рис. 36) полное напряжение в цепи запишется по теореме косинусов:

.

Отсюда

. (52)

Рис. 36

В этих выражениях U – подаваемое напряжение, U_к – напряжение на катушке, U_R – напряжение на омическом сопротивлении. Все три напряжения измеримы непосредственно. Далее, поскольку катушка и омическое сопротивление соединены последовательно, сила тока в них одинакова и определяется по формуле

, (53)

что позволяет обойтись без амперметра.

Экспериментальная часть

Оборудование: автотрансформатор; катушка; реостат; вольтметр 0-50 В; 2 вольтметра 0-150 В; сплошной и наборный сердечники.

Порядок выполнения работы

Задание 1. Измерение мощности катушки без сердечника.

В схеме на рис. 37 подаваемое в цепь напряжение регулируется автотрансформатором. В качестве омического сопротивления используется реостат.

1. Показания вольтметров снять при трех различных значениях тока в цепи, который задается напряжением на омическом сопротивлении (рекомендуем взять значения U_R = 30, 40 и 50 В). Результаты измерения занести в табл. 13.

Рис. 37

Таблица 13

Вид сердечника

UR, В

Uк

U

I, А

Сos φ

P, Вт

Rа, Ом

Pc, Вт

цена дел.

в дел.

в В

цена дел.

в дел.

в В

Без сердечника

Сплошной

Наборный

Задание 2. Измерение мощности катушки с сердечником.

1. Измерение мощности катушки с сердечником выполнить так же, как и в первом задании, и при тех же значениях тока в цепи, но с введенным в катушку сердечником: в одном случае – сплошным, в другом – наборным. Результаты измерения занести в табл. 13.

2. По измеренным напряжениям вычислить ток катушки I, коэффициент мощности cos j, потребляемую катушкой мощность P и ее активное сопротивление (согласно формулам (50) – (53)).

Полученные результаты занести в табл. 13.

Примечание. Величина P_с – есть мощность, идущая на нагревание сердечника (вследствие перемагничивания и токов Фуко), и вычисляется как разность потребляемых катушкой мощностей с сердечником и без него (при одинаковых значениях силы тока).

Контрольные вопросы и задания

1. Запишите закон Ома для переменного тока. Поясните смысл всех величин, входящих в закон.

2. Нарисуйте векторные диаграммы для идеальной катушки и катушки с заметным омическим (активным) сопротивлением в цепи переменного тока. Сделайте пояснения.

3. Постройте векторную диаграмму для схемы, использующейся в данной работе, и получите самостоятельно рабочую формулу (52).

4. Что понимается под эффективными значениями тока и напряжения?

5. Запишите и поясните формулы для вычисления мощности в цепи переменного тока.

6. Что такое токи Фуко? Когда они возникают? К чему приводят токи Фуко и перемагничивание сердечника катушки

Лабораторная работа 10 (12)