Электрическое поле диполя
Рассмотрим поле простейшей системы точечных зарядов. Простейшей системой точечных зарядов является электрический диполь. Электрическим диполем называется совокупность равных по величине, но противоположных по знаку двух точечных зарядов –q и +q, сдвинутых друг относительно друга на некоторое расстояние. Пусть 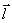 – радиус-вектор, проведенный от отрицательного заряда к положительному. Вектор
– радиус-вектор, проведенный от отрицательного заряда к положительному. Вектор
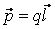
называется электрическим моментом диполя или дипольным моментом, а вектор 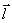 – плечом диполя. Если длина
– плечом диполя. Если длина 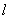 пренебрежимо мала по сравнению с расстоянием от диполя до точки наблюдения, то диполь называется точечным.
пренебрежимо мала по сравнению с расстоянием от диполя до точки наблюдения, то диполь называется точечным.
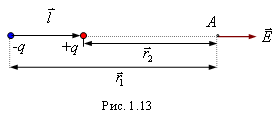 |
Вычислим электрическое поле электрического точечного диполя. Поскольку диполь точечный, то безразлично в пределах точности расчета от какой точки диполя отсчитывается расстояние r до точки наблюдения. Пусть точка наблюдения А лежит на продолжении оси диполя (рис. 1.13). В соответствии с принципом суперпозиции для вектора напряженности, напряженность электрического поля в этой точке будет равна
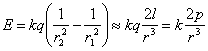 ,
,
при этом предполагалось, что 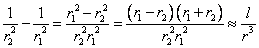 ,
, 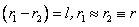 .
.
В векторной форме
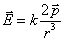 .
.
 |
Допустим теперь, что точка наблюдения А лежит на перпендикуляре, восстановленном к оси диполя из его центра О (рис. 1.13), тогда
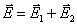 , , |
где 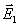 и
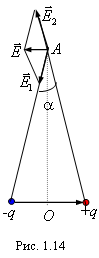
и 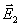 – напряженности полей, возбуждаемых точечными зарядами –q и +q. Из рис 1.14 видно, что вектор
– напряженности полей, возбуждаемых точечными зарядами –q и +q. Из рис 1.14 видно, что вектор 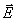 антипараллелен вектору
антипараллелен вектору 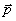 и его модуль для точечного диполя определится выражением
и его модуль для точечного диполя определится выражением
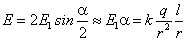 ,
,
здесь учтено, что при сделанных предположениях 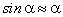 .
.
В векторной форме последнее выражение перепишется следующим образом
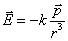 .
.
Не обязательно, чтобы перпендикуляр АО проходил через центр точечного диполя. В принятом приближении полученная формула остается верной и тогда, когда за точку О принята любая точка диполя.
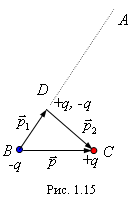 |
Общий случай сводится к разобранным частным случаям (рис. 1.15). Опустим из заряда +q перпендикуляр СD на линию наблюдения ВА. Поместим в точку D два точечных заряда +q и –q. Это не изменит поля. Но полученную совокупность четырех зарядов можно рассматривать как совокупность двух диполей с дипольными моментами 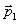 и
и 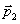 . Диполь
. Диполь 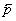 мы можем заменить геометрической суммой диполей
мы можем заменить геометрической суммой диполей 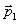 и
и 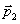 . Применяя теперь к диполям
. Применяя теперь к диполям 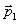 и
и 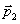 полученные ранее формулы для напряженности на продолжении оси диполя и на перпендикуляре, восстановленном к оси диполя, в соответствии с принципом суперпозиции получим:
полученные ранее формулы для напряженности на продолжении оси диполя и на перпендикуляре, восстановленном к оси диполя, в соответствии с принципом суперпозиции получим:
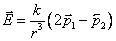 .
.
Учитывая, что 
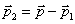 , получим:
, получим:

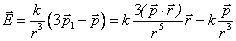 ,
,
здесь использовано, что 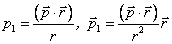 .
.
Таким образом, характерным для электрического поля диполя является то, что оно убывает во всех направлениях пропорционально 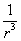 , то есть быстрее, чем поле точечного заряда.
, то есть быстрее, чем поле точечного заряда.
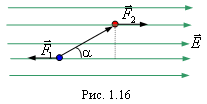 |
Рассмотрим теперь силы, действующие на диполь в электрическом поле. В однородном поле заряды +q и –q окажутся под действием равных по величине и противоположных по направлению сил 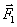 и
и 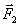 (рис. 1.16). Момент этой пары сил будет:
(рис. 1.16). Момент этой пары сил будет:
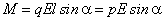 .
.
Момент 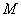 стремится повернуть ось диполя в положение равновесия, то есть в направлении вектора
стремится повернуть ось диполя в положение равновесия, то есть в направлении вектора 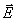 . Существует два положения равновесия диполя: когда диполь параллелен электрическому полю и антипараллелен ему. Первое положение будет устойчиво, а второе нет, так как в первом случае при малом отклонении диполя от положения равновесия возникнет момент пары сил, стремящийся вернуть его в исходное положение, во втором случае возникающий момент уводит диполь ещё дальше от положения равновесия.
. Существует два положения равновесия диполя: когда диполь параллелен электрическому полю и антипараллелен ему. Первое положение будет устойчиво, а второе нет, так как в первом случае при малом отклонении диполя от положения равновесия возникнет момент пары сил, стремящийся вернуть его в исходное положение, во втором случае возникающий момент уводит диполь ещё дальше от положения равновесия.
