Закон Ампера. Работа в магнитном поле

Одним из проявлений магнитного поля является его силовое воздействие на проводник с током, помещенный в магнитное поле. Ампером было установлено, что на проводник с током, помещенный в однородное магнитное поле, индукция которого В, действует сила, пропорциональная силе тока и индукции магнитного поля: dF = B I dl sin a,

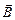где a – угол между векторами и 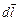. Или в векторной форме:

,

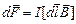где dl – малый участок проводника, имеющий направление, совпадающее с направлением тока]. Произведение Idl называют элементом тока. В случае прямолинейного проводника длиной l:

.

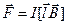Если 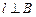, то F = I B l.

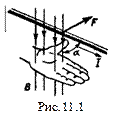
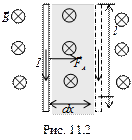
Для определения направления силы пользуются правилом левой руки: линии магнитной индукции входят в ладонь, четыре пальца совпадают с направлением тока, отогнутый большой палец укажет направление действия силы (рис.11.1).

Так как на проводник с током в магнитном поле действует сила Ампера, то под ее действием магнитным полем совершается работа по перемещению проводника с током. Для определения этой работы рассмотрим проводник длиной l с током I, помещенный в однородное магнитное поле, перпендикулярное плоскости контура (рис. 11.2). Под действием силы Ампера F = F_А = I B l проводник переместится параллельно самому себе на расстояние dx. Работа, совершаемая магнитным полем, равна :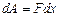

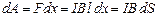(т.к. ).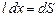

У нас направление поля В перпендикулярно площадке dS. В общем случае берем составляющую В_n: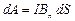

Введем понятие потока вектора магнитной индукции (магнитный поток):

Ф = В S cos a,

где a – угол между вектором нормали к поверхности и вектором магнитной индукции, или 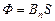. В случае неоднородного поля рассматривают магнитный поток через элементарную площадку: 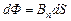, затем суммируют по всей площади S:

.

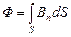[Ф] = Вб (вебер).

Тогда работа по перемещению проводника с током в магнитном поле: 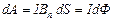Þ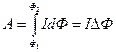

где DФ = Ф₂ – Ф₁ – изменение магнитного потока.

Действие магнитного поля на движущиеся заряды.

Сила Лоренца.

Движущиеся электрические заряды создают вокруг себя магнитное поле, которое распространяется в вакууме со скоростью света. При движении заряда во внешнем магнитном поле возникает силовое взаимодействие магнитных полей, определяемое по закону Ампера. Процесс взаимодействия магнитных полей исследовался Лоренцем, который вывел формулу для расчета силы, действующей со стороны магнитного поля на движущуюся заряженную частицу.

Силу, действующую со стороны магнитного поля на движущийся заряд, можно найти исходя из закона Ампера. Пусть по проводнику длиной dl за промежуток времени dt проходит п одинаковых зарядов величиной dq, т.е. через проводник протекает ток, сила которого: 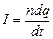. Согласно закону Ампера, на n dq зарядов будет действовать сила .

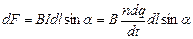Сила, с которой поле действует на каждый заряд, равна:

,

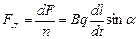где 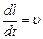–скорость движения заряда, a– угол между вектором скорости заряда и вектором магнитной индукции. Сила, действующая со стороны магнитного поля на движущийся заряд, равна

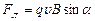
и называется силой Лоренца. Эта сила перпендикулярна векторам 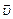и 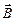. Направление силы Лоренца, действующей на положительный заряд, определяется по правилу левой руки. С изменением знака заряда направление силы изменяется на противоположное.

В векторном виде сила Лоренца записывается:

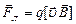
Анализируя полученное выражение, можно сделать выводы:

- если скорость заряда u= 0, то F_л = 0, т. е. магнитное поле не действует на неподвижную заряженную частицу;

- если a= 0, sin a = 0, то F_л = 0, т. е. если частица движется так, что
вектор скорости параллелен вектору магнитной индукции , то со стороны магнитного поля сила не действует.

Так как сила Лоренца всегда направлена перпендикулярно вектору скорости летящей частицы, то она не изменяет величину скорости, а изменяет лишь направление движения частиц. Если заряженная частица движется в однородном магнитном поле, вектор индукции которого перпендикулярен направлению скорости заряженной частицы, то сила Лоренца искривляет траекторию движения, выполняя роль центростремительной силы. Действие этой силы не приводит к изменению энергии заряженной частицы, т.е. эта сила не совершает работы.

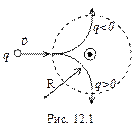
Попадание летящей частицы в магнитное поле вызывает изменение ее траектории в зависимости от знака заряда (рис. 12.1). На рис. вектор индукции магнитного поля направлен перпендикулярно плоскости чертежа (на нас). Частица будет двигаться по окружности, радиус R которой можно определить из равенства центростремительной силы и силы Лоренца: 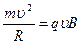,откуда .

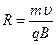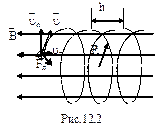Если частица движется под углом b к линиям В, то траектория движения частицы будет винтовой линией (спиралью) (рис.12.2). Шаг h спирали определяется u_t – тангенциальной составляющей скорости uчастицы. Радиус спирали зависит от u_n – нормальной составляющей скорости u.

Когда электрический заряд движется одновременно в электрическом и магнитном полях, то результирующая сила, действующая на частицу, равна: .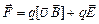

В этом случае сила имеет две составляющие: от воздействия магнитного и электрического полей. Между этими составляющими имеется принципиальная разница. Электрическое поле изменяет величину скорости, а следовательно, и кинетическую энергию частицы, однородное магнитное поле изменяет только направление ее движения.