Внутренняя энергия газа U из чего она складывается связь с теплоемкостью и температурой

Внутренняя энергия — это кинетическая энергия хаотического (теплового) движения частиц системы (молекул, атомов, ядер, электронов) и потенциальная энергия взаимодействия этих частиц.

Согласно закону Джоуля, выведенному эмпирически, внутренняя энергия идеального газа не зависит от давления или объёма. Исходя из этого факта, можно получить выражение для изменения внутренней энергии идеального газа. По определению молярной теплоёмкости при постоянном объёме, 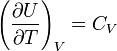. Так как внутренняя энергия идеального газа является функцией только от температуры, то

.

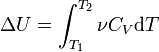Эта же формула верна и для вычисления изменения внутренней энергии любого тела, но только в процессах при постоянном объёме (изохорных процессах); в общем случае 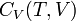является функцией и температуры, и объёма.

Если пренебречь изменением молярной теплоёмкости при изменении температуры, получим:

,

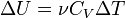где 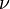— количество вещества, 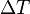— изменение температуры.

Для идеального газа внутренняя энергия равна:

,

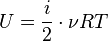где 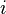- количество степеней свободы, 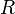- универсальная газовая постоянная.

9. Энтальпия : физический смысл, формула, единица измерения

Энтальпи́я, также тепловая функция и теплосодержание — термодинамический потенциал, характеризующий состояние системы в термодинамическом равновесии при выборе в качестве независимых переменных давления, энтропии и числа частиц.

Проще говоря, энтальпия — это та энергия, которая доступна для преобразования в теплоту при определенном постоянном давлении.

Если термомеханическую систему рассматривать как состоящую из макротела (газа) и поршня площадью S с грузом весом Р = pS, уравновешивающего давление газа р внутри сосуда, то такая система называется расширенной.

Энтальпия или энергия расширенной системы Е равна сумме внутренней энергии газа U и потенциальной энергии поршня с грузомE_пот = pSx = pV

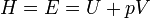
Таким образом, энтальпия в данном состоянии представляет собой сумму внутренней энергии тела и работы, которую необходимо затратить, чтобы тело объёмом V ввести в окружающую среду, имеющую давление р и находящуюся с телом в равновесном состоянии. Энтальпия системы H — аналогично внутренней энергии и другим термодинамическим потенциалам — имеет вполне определенное значение для каждого состояния, т. е. является функцией состояния. Следовательно, в процессе изменения состояния

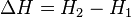
Изменение энтальпии (или Тепловой эффект химической реакции) не зависит от пути процесса, определяясь только начальным и конечным состоянием системы. Если система каким-либо путём возвращается в исходное состояние (круговой процесс), то изменение любого её параметра, являющегося функцией состояния, равно нулю, отсюда 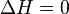, или же

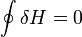
Дифференциал энтальпии, выраженный в собственных переменных — через энтропию S и давление p:

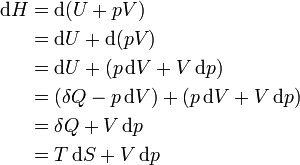
Поскольку в квазиравновесных процессах 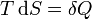— количество теплоты, подведенной к системе, отсюда вытекает физический смысл введения понятия энтальпии: ее изменение — это тепло, подведенное к системе в изобарическом процессе (при постоянном давлении). Практическое применение этой функции основано на том, что множество химических процессов в реальных или лабораторных условиях реализуются именно при постоянном (атмосферном) давлении, когда резервуар открыт. Так, энтальпия образования — количество энергии, которое выделяется или поглощается при образовании сложного вещества из простых веществ.

Все химические реакции сопровождаются выделением (экзотермические) или поглощением (эндотермические) тепла. Мерой теплоты реакции служит изменение энтальпии ΔН, которая соответствует теплообмену при постоянном давлении. В случае экзотермических реакций система теряет тепло и ΔН — величина отрицательная. В случае эндотермических реакций система поглощает тепло и ΔН — величина положительная.

Энтальпией системы удобно пользоваться в тех случаях, когда в качестве независимых переменных, определяющих состояние системы, выбирают давление р и температуру Т

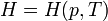
В этом случае изменение энтальпии в изобарическом процессе практически удобно рассчитывать, зная теплоемкость при постоянном давлении 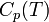(термохимический закон Кирхгофа):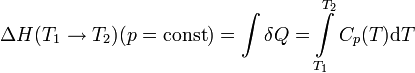

При этом используется эмпирическое разложение теплоёмкости в ряд по степеням Т:

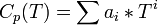
Энтальпия — величина аддитивная (экстенсивная), т. е. для сложной системы равна сумме энтальпий её независимых частей 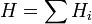. Подобно другим термодинамическим потенциалам, энтальпия определяется с точностью до постоянного слагаемого, которому в термодинамике часто придают произвольные значения (например, при расчете и построении тепловых диаграмм). При наличии немеханических сил величина энтальпии системы равна

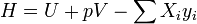
где 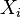— обобщённая сила; 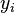— обобщённая координата.

Инвариантная энтальпия в релятивистской термодинамике

При построении релятивистской термодинамики (с учетом специальной теории относительности) обычно наиболее удобным подходом является использование так называемой инвариантной энтальпии — для системы, находящейся в некотором сосуде.

При этом подходе температура 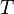определяется как лоренц-инвариант. Энтропия 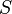— также инвариант. Поскольку стенки влияют на систему, наиболее естественной независимой переменной является давление 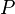, в связи с чем в качестве термодинамического потенциала удобно брать именно энтальпию^[1].

Для такой системы «обычная» энтальпия и импульс системы 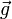образуют 4-вектор, и за определение инвариантной энтальпии, одинаковой во всех системах отсчёта, берётся инвариантная функция этого 4-вектора:

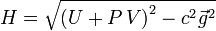
Основное уравнение релятивистской термодинамики записывается через дифференциал инвариантной энтальпии следующим образом:

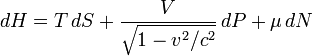
Пользуясь этим уравнением, можно решить любой вопрос термодинамики движущихся систем, если известна функция .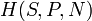

10.Энтропия : физический смысл, формула, единица измерения

Энтропи́я (от др.-греч. ἐντροπία — поворот, превращение) — в естественных науках мера неупорядоченности системы, состоящей из многих элементов. В частности, в статистической физике — мера вероятности осуществления какого-либо макроскопического состояния; в теории информации — мера неопределённости какого-либо опыта (испытания), который может иметь разные исходы, а значит, и количество информации; в исторической науке, для экспликации феномена альтернативности истории (инвариантности ивариативности исторического процесса).

Энтропия в информатике — степень неполноты, неопределённости знаний.

Энтропия — мера неупорядоченности системы.

Явление, обратное энтропии, именуется негэнтропией.

Понятие энтропии впервые было введено Клаузиусом в термодинамике в 1865 году для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального. Определённая как сумма приведённых теплот, она является функцией состояния и остаётся постоянной при замкнутых обратимых процессах, тогда как в необратимых — её изменение всегда положительно.

,

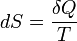где 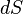— приращение энтропии; 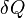— минимальная теплота, подведённая к системе; 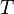— абсолютная температура процесса.

· Термодинамическая энтропия — термодинамическая функция, характеризующая меру неупорядоченности термодинамической системы, то есть неоднородность расположения и движения её частиц.