Квантомеханическое представление свободно движущейся частицы.

При движении свободной частицы (U(x) = 0) ее полная энергия совпадает с кинетической. Для свободной частицы, движущейся вдоль оси х, уравнение Шредингера для стационарных состояний примет вид 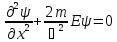.Прямой подстановкой можно убедиться в том, что частным решением уравнения i является функция 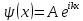, где A=const иk = const, с собственным значением энергии 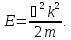Функция 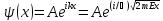представляет собой только координатную часть волновой функции 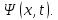Поэтому зависящая от времени волновая функция, согласно 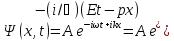, (219.3) (здесь 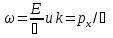Функция представляет собой плоскую монохроматическую волну де Бройля). Из выражения 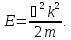следует, что зависимость энергии от импульса 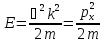оказывается обычной для нерелятивистских частиц. Следовательно, энергия свободной частицы может принимать любые значения (так как волновое числоk может принимать любые положительные значения), т. е. ее энергетический спектр является непрерывным.Таким образом, свободная квантовая частица описывается плоской монохроматической волной де Бройля. Этому соответствует не зависящая от времени плотность вероятности обнаружения частицы в данной точке пространства.

Квантовомеханическое описание частиц в бесконечно глубокой потенциальной яме

В методичке

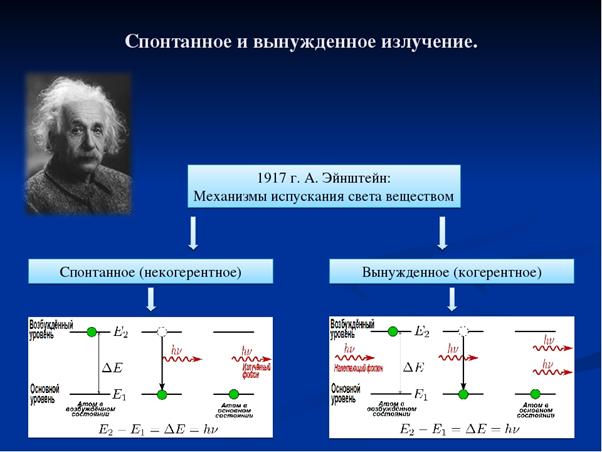
Резонансное поглощение –это процесс в котором атом поглощает фотон и одновременно переходит с нижнего уровня Ei на верхний уровень Ek.

Hv=Ek-Ei

Ширина спектральной линии— интервал частот или интервал длин волн, характеризующий спектральные линии в излучениях квантовых систем.^[1] Ширина линии измеряется по половине от максимальной интенсивности (см. Полуширина).^[2]

Ширина спектральной линии — интервал частот или интервал длин волн, характеризующий спектральные линии в излучениях квантовых систем.^[1] Ширина линии измеряется по половине от максимальной интенсивности (см. Полуширина).^[2]

Следовательно, ширина спектральной линии

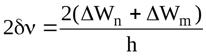. (6)

Коэффициенты Эйнштейна

В процессах испускания и поглощения фотонов, как правило, участвует огромное число атомов, поэтому эти процессы описываются статистически с помощью теории вероятностей.

Вероятностью испускания (поглощения) называется среднее число фотонов, испускаемых (поглощаемых) одним атомом в единицу времени.

Вероятность перехода атома с уровня m на уровень n будем обозначать через W_mn. Вероятность спонтанного перехода постоянна для данной пары уровней и равна 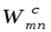= ^A_mn. Вероятность вынужденного перехода пропорциональна спектральной объемной плотности энергии (см. (1.1)) w вынуждающего излучения с частотой =(E_m-E_n)/h: 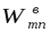^=B_mn^{w. Коэффициенты A}_mn ^иB_mn ^{называются} коэффициентами Эйнштейна. Они не зависят от направления процесса, и определяются только начальным и конечным состояниями атома: A_mn = A_nm и B_mn = B_nm..

Квантовое усиление и генерация света. Инверсная населенность уровней (методы осуществления инверсии населенностей). Лазеры. Рубиновый и гелий-неоновый лазеры.