Второго начала термодинамики

При реализации системой необратимых термодинамических процессов ее конечное состояние отличается от начального заметно большей величиной энтропии. Причем эта разность тем больше, чем выше степень необратимости присутствующих при реализации процесса диссипативных моментов. Это означает, что каждое последующее состояние системы более вероятно предшествующему.

Пусть система состоит из N одинаковых молекул, где их число достаточно велико. В этом случае одно и тоже макроскопическое состояние термодинамической системы ( 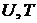) может обеспечиваться различным распределением энергии между отдельно взятыми частицами – молекулами, то есть через различные ее микросостояния.

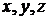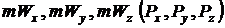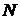Каждое конкретно взятое микросостояние отличается от других значениями координат и импульсов всех молекул, из которых состоит система. Рассмотрим некоторое “замороженное” микросостояние системы. Тогда из всех 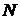молекул их 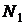число будет иметь энергию 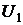, 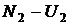и т.д. Где 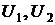– энергетические уровни конкретных молекул–частиц молекулярной системы. В соответствии с тем, что мы рассматривали микросостояния, обеспечивающие конкретное макросостояние, должно выполняться очевидное равенство

.

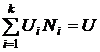Общее число микросостояний, обеспечивающих данное макросостояние будет равно общему числу перестановок N ! поделенному на число перестановок молекул внутри каждой из характерных по энергиям групп

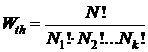. (11.4)

Величину 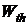по предложению Планка называют термодинамической вероятностью. Численное значение 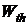больше единицы во много раз. Она характеризует возможность реализации определенного распределения молекул по энергиям или вероятность данного молекулярного состояния.

Хаотичность теплового движения молекул обуславливает равновероятность каждого из микросостояний, отвечающему условию 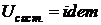. Это означает, что частота появления микросостояний с одинаковым распределением молекул по энергиям будет тем большей, чем больше число способов, обеспечивающих данное распределение, следовательно, тем больше термодинамическая вероятность данного микросостояния. Таким образом, состояние системы с максимальным значением термодинамической вероятности представляют собой равновесные состояния системы. Все другие состояния системы, вероятность которых меньше максимальной будут неравновесными.

Отношение термодинамической вероятности данного молекулярного состояния к общему числу возможных микросостояний системы представляет собой вероятность W данного молекулярного состояния системы. В этом случае очевидно, что W<1.

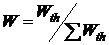. (11.5)

Зная вероятность 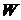или термодинамическую вероятность 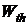каждого из молекулярных состояний системы, легко вычислить среднее значение любой величины В, зависящей от состояния системы

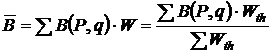, (11.6)

где В – некоторая физическая величина, зависящая от координат и импульсов молекул данной системы. Суммирование в (11.6) производится по всем молекулярным состояниям.

Формула Больцмана

Рассмотрим равновесный изотермический процесс изменения состояния системы, в результате которого объем системы 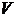получает приращение 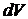и становится равным 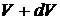, а внутренняя энергия системы изменится на величину произведенной работы 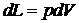. При этом произойдет дополнительное изменение внутренней энергии системы, связанное с изменением распределения молекул по энергиям. Энергия каждого микросостояния равна внутренней энергии 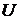системы. Тогда изменение внутренней энергии 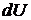при изменении числа микросостояний на 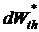будет пропорционально относительному изменению числа микросостояний 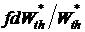. Множитель f введен из соображений размерности 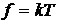. Индекс «*»означает, что рассуждение относится к равновесным состояниям. Тогда полное изменение внутренней энергии молекулярной системы при изотермическом процессе

.

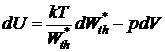В соответствии с первым началом термодинамики

.

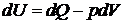Приравнивая правые части получим

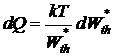. (11.7)

Из последнего выражения (11.7) следует вывод, что подведенная к системе из вне энергия затрачивается на изменение распределения молекул по энергии. Т.о. подведенная энергия связана с перераспределением вероятностей микросостояний. Если процесс равновесный, то 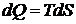, а значит

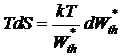или .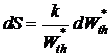

Или после интегрирования

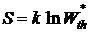. (11.8)

В изолированной системе любое из состояний соответствует одному и тому же значению внутренней энергии, поэтому полученная зависимость может быть распределена и на неравновесные состояния

.

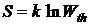Из последнего выражения следует, что энтропия всегда положительна ( 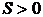), так как 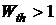. Значения термодинамической вероятности и вероятности состояния отличаются на величину постоянного множителя, тогда

.

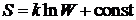Энтропия изолированной системы пропорциональна натуральному логарифму вероятности состояния.

Последнее выражение принято называть формулой Больцмана. Из формулы Больцмана не следует, что энтропия - величина аддитивная.

Рассмотрим составную систему, для которой вероятность W данного состояния равна произведению вероятностей состояний 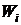, составных частей 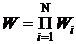. После логарифмирования получим

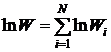
или 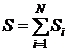. (11.9)

Зависимость (11.9) отражает аддитивность энторопии.