Изотермический процесс изменения состояния водяного пара
Если изотермический процесс начинается в двухфазной области, то он определяется двумя начальными параметрами один из которых позволит найти соотношение фаз, и одним любым конечным параметром отличным от температуры. Удобнее всего и нагляднее изотермический процесс представляется графически в 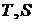 – диаграмме. Пусть начальная точка, к примеру, лежит в области влажного насыщенного пара. При изотермическом перегреве пара, как видно из
– диаграмме. Пусть начальная точка, к примеру, лежит в области влажного насыщенного пара. При изотермическом перегреве пара, как видно из 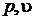 диаграммы (рисунок 9.6), его давление уменьшается
диаграммы (рисунок 9.6), его давление уменьшается 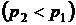 . Это не позволяет использовать изотермический перегрев пара в циклах паросиловых установок, работающих на перегретом паре.
. Это не позволяет использовать изотермический перегрев пара в циклах паросиловых установок, работающих на перегретом паре.
Площадь под процессом в 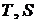 – диаграмме численно равна подводимой теплоте
– диаграмме численно равна подводимой теплоте 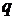 .
.
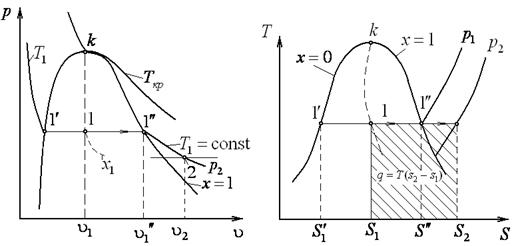 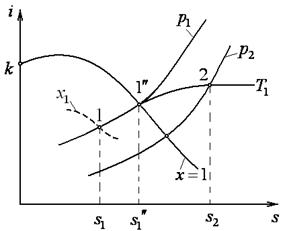 Рисунок 9.6 P, Рисунок 9.6 P, 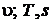 и и 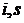 - диаграммы изотермического процесса изменения состояния пара - диаграммы изотермического процесса изменения состояния пара |
Изменение внутренней энергии в течении процесса
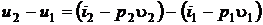 (9.29)
(9.29)
Удельную теплоту подведенную в процессе можно найти через изменение энтропии
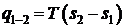 (9.30)
(9.30)
Удельная работа расширения из первого начала запишется как разность подведенной теплоты и изменение внутренней энергии в процессе.
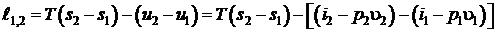 . (9.31)
. (9.31)
Адиабатный процесс изменения состояния водяного пара
Рассмотрим равновесный адиабатный процесс (идеальная адиабата), при протекании которого энтропия в процессе остается неизменной 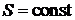 . Поэтому во всякой энтропийной диаграмме идеальная адиабата изображается отрезком вертикальной прямой. Если начальное состояние пара на
. Поэтому во всякой энтропийной диаграмме идеальная адиабата изображается отрезком вертикальной прямой. Если начальное состояние пара на 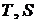 – диаграмме расположено левее адиабаты
– диаграмме расположено левее адиабаты 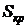 , то при адиабатном расширении жидкости (процесс a-b) давление снижается и жидкость превращается во влажный насыщенный пар как показано на
, то при адиабатном расширении жидкости (процесс a-b) давление снижается и жидкость превращается во влажный насыщенный пар как показано на 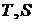 – диаграмме, а паросодержание становится равным
– диаграмме, а паросодержание становится равным 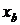 , т. е. часть жидкости переходит в состояние пара.
, т. е. часть жидкости переходит в состояние пара.
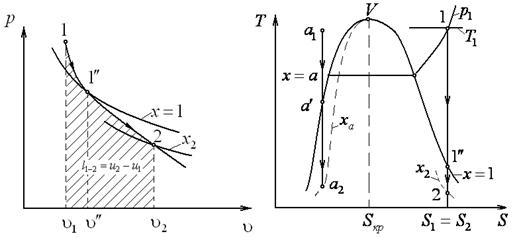 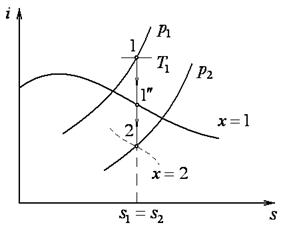 Рисунок 9.7 Рисунок 9.7 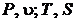 и и 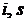 - диаграммы адиабатного процесса изменения состояния пара - диаграммы адиабатного процесса изменения состояния пара |
При таком же расширении перегретого пара (рисунок 9.7) он сначала переходит в сухой насыщенный пар (точка 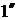 ), а затем во влажный насыщенный пар (точка 2).
), а затем во влажный насыщенный пар (точка 2).
Линия постоянной степени сухости пара (паросодержания) x = 0,5 в диаграмме 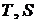 имеет почти вертикальную ориентацию и разделяет область влажного пара на две части. В левой части, т. е. при x < 0,5, при адиабатном расширении влажного насыщенного пара паросодержание увеличивается, а в правой – уменьшается.
имеет почти вертикальную ориентацию и разделяет область влажного пара на две части. В левой части, т. е. при x < 0,5, при адиабатном расширении влажного насыщенного пара паросодержание увеличивается, а в правой – уменьшается.
Для адиабатного процесса энергетика цикла ( 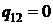 ) определяется очевидными зависимостями
) определяется очевидными зависимостями
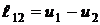 (9.32)
(9.32)
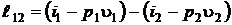 (9.33)
(9.33)
Адиабатный процесс приближенно может быть описан уравнением 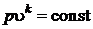 .
.
Для влажного пара с начальным паросодержанием показатель адиабаты определяют по формуле
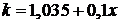 ,
,
Таким образом для сухого пара 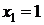 , k = 1,135
, k = 1,135
Для перегретого пара k = 1,3
Записанные выражения и численные значения справедливы лишь при 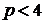 МПа. В уравнении адиабаты для пара показатель степени не является отношением теплоемкостей
МПа. В уравнении адиабаты для пара показатель степени не является отношением теплоемкостей 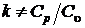 , и находиться как эмпирический показатель степени.
, и находиться как эмпирический показатель степени.
Примеры решения задач на процессы с водяным паром.
Пример 1.
Сосуд постоянного объема 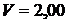 дм3 содержит сухой насыщенный водяной пар при температуре
дм3 содержит сухой насыщенный водяной пар при температуре 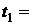 250 °C, охлаждающийся до
250 °C, охлаждающийся до 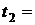 130 °C. Определите массу конденсирующегося водяного пара и объем занимаемый конденсатом в конечном состоянии, а также тепло, отдаваемое при охлаждении.
130 °C. Определите массу конденсирующегося водяного пара и объем занимаемый конденсатом в конечном состоянии, а также тепло, отдаваемое при охлаждении.
ДАНО 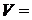 2,0 дм 2,0 дм 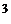 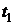 =250 =250  C C 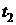 =130 =130  C C | С.И 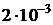 м м 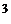 523 К 403 К 523 К 403 К |
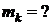 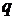 =? =? |
Анализ
Задача по термодинамике на процессы с водяным паром. Конечное состояние пара будет в двухфазной области влажного пара. Процесс охлаждения изохорный и поэтому работа расширения 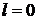 .
.
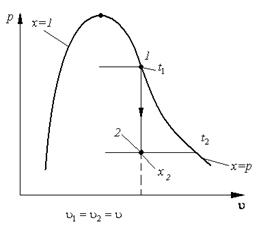 Рисунок 9.3 К выводу правила рычага. Рисунок 9.3 К выводу правила рычага. |
Решение
Найдем массу сконденсировавшегося пара
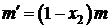 , где
, где 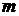 общая масса влажного пара в точке 2;
общая масса влажного пара в точке 2;
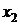 – паросодержание в точке 2.
– паросодержание в точке 2.
Найдем массу пара в начальном состоянии.
По условию задачи эта масса сухого насыщенного пара в точке 1, следовательно
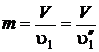 .
.
Удельный объем сухого насыщенного пара 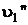 берем из таблиц для воды и водяного пара при
берем из таблиц для воды и водяного пара при 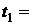 250 °C,
250 °C, 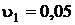 м3/кг, тогда
м3/кг, тогда
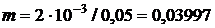 кг.
кг.
Т. к. пар охлаждается изохорно, то 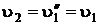 .
.
Найдем степень сухости в конце процесса охлаждения
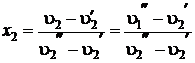
Значения 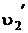 и
и 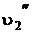 при
при 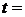 130 °C, вновь находим из таблиц
130 °C, вновь находим из таблиц
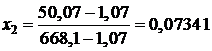 .
.
Конечное паросодержание мало, т. к. большая часть пара конденсируется
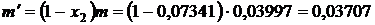 кг.
кг.
Однако конденсат занимает лишь небольшую часть объема сосуда
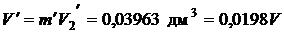 ,
,
т. е. около 98 % объема сосуда заполнено сухим насыщенным паром, масса которого составляет лишь 7,34 % от общей массы. По Первому закону термодинамики для закрытой системы запишем
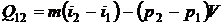 .
.
Из таблиц находим 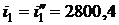 кДж/кг.
кДж/кг.
Для энтальпии влажного пара в конце охлаждения
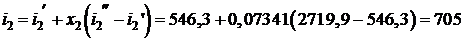 кДж/кг.
кДж/кг.
Пример 2.
Определить состояние и калорические параметры водяного пара при 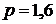 МПа и
МПа и 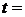 500 °C.
500 °C.
ДАНО 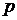 =1,6 мПа =1,6 мПа 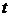 =500 =500 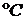 | С.И 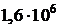 Па 723 К Па 723 К |
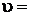 ? ? 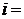 ? s=? ? s=? 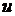 =? =? |
Анализ
Задачи на определение параметров состояния пара по его двум исходным начальным параметрам давлению и температуре.
Воспользовавшись таблицами водяного пара или 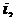
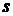 - диаграммой найдем в какой области состояние пара находится точка, определяющая его первоначальное состояние исходя из данных по условию.
- диаграммой найдем в какой области состояние пара находится точка, определяющая его первоначальное состояние исходя из данных по условию.
Воспользуемся заданным давлением и по таблицам находим, что температура насыщающих паров при этом давлении равна 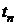
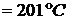 . Таким образом температура пара
. Таким образом температура пара 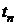 >
> 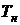 , а значит пар находится в температурной области и задачу решать лучше с использованием
, а значит пар находится в температурной области и задачу решать лучше с использованием 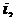
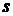 - диаграммы.
- диаграммы.
 |
Решение
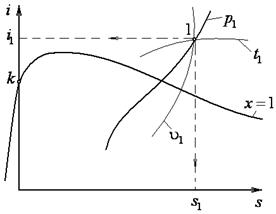
Исходное состояние находится как точка пересечения изобары 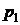 с изотермой
с изотермой 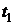 . Проводя соответствующие линии из "1"
. Проводя соответствующие линии из "1" 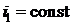 , а также
, а также 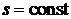
 найдем по соответствующим шкалам значения
найдем по соответствующим шкалам значения 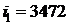 кДж/кг;
кДж/кг; 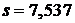 кДж/(кг×К). Удельный объем используя экстраполяции либо интерполяции находим через две проходящие с двух сторон от точки приведенный на диаграмме изохоры
кДж/(кг×К). Удельный объем используя экстраполяции либо интерполяции находим через две проходящие с двух сторон от точки приведенный на диаграмме изохоры 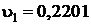 м3/кг.
м3/кг.
Внутреннюю энергию перегретого пара в точке 1 определим воспользовавшись известным соотношением
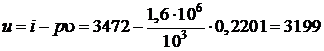 кДж/кг.
кДж/кг.
Пример 3.
Перегретый пар при 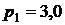 МПа и
МПа и 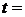 350 °C адиабатно расширяется до
350 °C адиабатно расширяется до 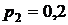 МПа. Пользуясь
МПа. Пользуясь 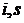 – диаграммой, определить
– диаграммой, определить 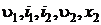 , работу и изменение внутренней энергии в этом процессе.
, работу и изменение внутренней энергии в этом процессе.
ДАНО 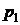 =1,6 мПа =1,6 мПа 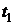 =500 =500 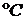 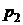 =0,2 мПа =0,2 мПа 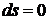 | С.И 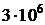 Па Па 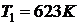 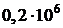 Па Па 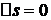 |
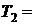 ? ? 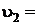 ? ? 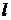 =? =? 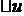 =? =? |
Анализ
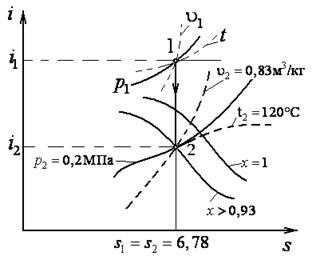
Задача из термодинамики на адиабатный процесс перегретого пара. Для ее решения удобно воспользоваться 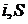 – диаграммой. Конечное состояние пара в процессе будет однозначно определяться точкой пересечения вертикали
– диаграммой. Конечное состояние пара в процессе будет однозначно определяться точкой пересечения вертикали 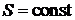 и изобары
и изобары 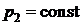 . Требуемые к определению параметры легко находятся если воспользоваться
. Требуемые к определению параметры легко находятся если воспользоваться 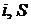 – диаграммой водяного пара и соответствующими зависимостями для расчета изменения внутренней энергии и работы расширения.
– диаграммой водяного пара и соответствующими зависимостями для расчета изменения внутренней энергии и работы расширения.
 |
Решение
Изобразим процесс расширения пара по адиабате в 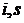 – диаграмме. Начальную точку
– диаграмме. Начальную точку 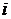 находим как пересечение изобары
находим как пересечение изобары 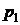 с изотермой
с изотермой 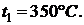 Затем отпускаем перпендикуляр до пересечения С изобарой
Затем отпускаем перпендикуляр до пересечения С изобарой 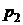 и находим точку пересечения 2, отражающей состояние пара по завершению адиабатного процесса.
и находим точку пересечения 2, отражающей состояние пара по завершению адиабатного процесса.
Пользуясь 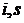 – диаграммой и найденными точками по диаграмме определим численные значения параметров:
– диаграммой и найденными точками по диаграмме определим численные значения параметров: 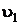 ,
, 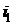 ,
, 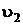 ,
, 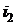 ,
, 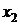 . Используя найденные и заданные величины рассчитываем калорические величины: работу, изменение внутренней энергии.
. Используя найденные и заданные величины рассчитываем калорические величины: работу, изменение внутренней энергии.
Точка 1: 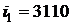 кДж/кг;
кДж/кг; 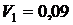 м3/кг;
м3/кг; 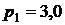 МПа;
МПа; 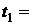 500 °C;
500 °C;
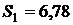 кДж/(кг×К).
кДж/(кг×К).
Точка 2: 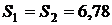 кДж/(кг×К);
кДж/(кг×К); 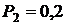 МПа;
МПа; 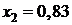 ;
; 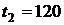 °C;
°C;
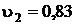 м3/кг;
м3/кг; 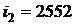 кДж/кг.
кДж/кг.
В адиабатном процессе теплообмен отсутствует 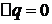 . Тогда, в соответствии с первым началом термодинамики, будет иметь
. Тогда, в соответствии с первым началом термодинамики, будет иметь
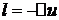
Найдем изменение внутренней энергии в процессе
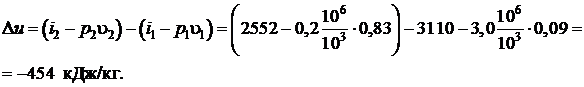
Тогда искомая работа в процессе найдется как изменение внутренней энергии
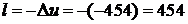 кДж/кг.
кДж/кг.
Влажный газ.
10.1 Основные понятия и определения
Строго говоря, в природе в естественных условиях сухих газов не существует. Воздух, продукты сгорания топлива в тепловых двигателях всегда содержат определенное количество водяных паров. Небольшое содержание пара может при определенных условиях оказать заметное влияние на термодинамические свойства газа. В том же случае, когда массовая доля пара в смеси с сухим газом значительна, изменение состояния необходимо рассчитывать с учетом взаимного влияния свойств газов, входящих в нее. Термодинамические процессы с влажным газом встречаются в инженерной практике, когда рассчитываются процессы сушки, кондиционирования и вентиляции, а также процессы адиабатного расширения и сжатия при наличии фазовых переходов, хотя бы одного из компонентов.
Влажным газом называется смесь сухого газа и водяного пара, хотя в некоторых случаях газ может быть увлажнен и парами другой жидкости – эфира, спирта, аммиака и т. д. Смесь сухого воздуха и водяного пара называют влажным воздухом. Если влажный газ находится при относительно невысоком давлении, то можно считать, что его состояние описывается уравнением Клапейрона-Менделеева. Т.е его можно считать идеальным и, следовательно, для него справедлив закон Дальтона
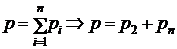 ,
,
где 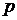 – давление смеси,
– давление смеси, 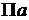 ;
; 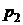 – парциальное давление сухого газа,
– парциальное давление сухого газа, 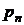 – парциальное давление пара.
– парциальное давление пара.
Состояние пара во влажном воздухе определятся парциальным давлением пара и температурой парогазовой смеси. Если пар в смеси сухой насыщенный, то такой влажный газ (воздух) принято называть насыщенным газом (воздухом). В этом случае парциальное давление пара 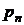 в смеси равно давлению насыщенных паров
в смеси равно давлению насыщенных паров 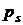 , при температуре смеси
, при температуре смеси 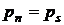 . Иначе, температура пара равна температуре кипения
. Иначе, температура пара равна температуре кипения 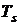 , определяемой по парциальному давлению пара
, определяемой по парциальному давлению пара 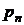 ; т. е.
; т. е. 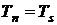 .
.
В случае, когда 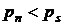 , а
, а 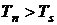 пар в смеси находится в перегретом состоянии и газ называется ненасыщенным.
пар в смеси находится в перегретом состоянии и газ называется ненасыщенным.
Температуру, при которой в процессе изобарного охлаждения парциальное давление пара 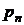 становится равным давлению насыщения
становится равным давлению насыщения 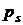 , называется температурой точки росы.
, называется температурой точки росы.
Парциальное давление пара т. о. подчиняется очевидному неравенству
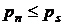 .
.
Это означает, что массовая доля пара в смеси с воздухом определяется парциальным давлением пара, которое не может быть больше чем давление насыщающих паров 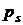 , при температуре влажного газа (воздуха).
, при температуре влажного газа (воздуха).
Содержание влаги в воздухе принято оценивать абсолютной и относительной влажностями.
Абсолютной влажностью 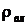 называют отношение массы влаги (в общем случае паровой, жидкой и твердой фаз – тумана и кристалликов льда) к ее объему или к равному ей объему влажного газа (воздуха).
называют отношение массы влаги (в общем случае паровой, жидкой и твердой фаз – тумана и кристалликов льда) к ее объему или к равному ей объему влажного газа (воздуха).
 (10.1)
(10.1)
где 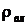 – абсолютная влажность, кг/м3;
– абсолютная влажность, кг/м3; 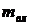 – масса влаги, кг;
– масса влаги, кг; 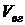 – объем влажного газа, м3. Если влага присутствует лишь в виде пара, то
– объем влажного газа, м3. Если влага присутствует лишь в виде пара, то 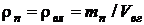 .
.
Относительной влажностью 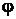 называют отношение плотности пара при его парциальном давлении
называют отношение плотности пара при его парциальном давлении 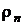 и температуре смеси к плотности сухого насыщенного пара, при той же температуре
и температуре смеси к плотности сухого насыщенного пара, при той же температуре
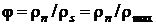 . (10.2)
. (10.2)
При повышении температуры относительная влажность уменьшается. При этом абсолютная влажность остается неизменной.
Запишем уравнение состояния для пара в смеси с воздухом
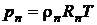 или
или 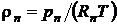
и 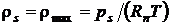 .
.
Или, после подстановки в выражение для 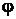
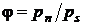 . (10.3)
. (10.3)
Относительная влажность 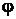 может принимать значения
может принимать значения 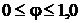 или
или 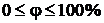
Значение 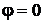 соответствует сухому воздуху; при
соответствует сухому воздуху; при 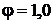 – сухому насыщенному пару.
– сухому насыщенному пару.
Массовым влагосодержанием называют отношение массы влаги 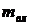 , к массе сухого газа (воздуха)
, к массе сухого газа (воздуха) 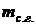
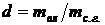 . (10.4)
. (10.4)
Мольным влагосодержанием 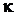 называют отношение количества вещества влаги
называют отношение количества вещества влаги 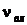 в газе (воздухе) к количеству вещества сухого газа
в газе (воздухе) к количеству вещества сухого газа 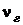
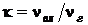 . (10.5)
. (10.5)
Вспоминая, что 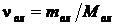 , а
, а 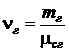 , где
, где 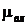 и
и 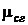 – мольные массы влаги и сухого газа, после подстановки получим
– мольные массы влаги и сухого газа, после подстановки получим 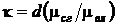 .
.
Для влажного воздуха, в частности получим 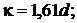
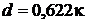
Массовой долей пара 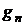 во влажном воздухе называют отношение массы пара
во влажном воздухе называют отношение массы пара 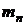 к массе влажного газа (воздуха)
к массе влажного газа (воздуха) 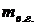
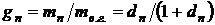 (10.6)
(10.6)
Тогда для массового влагосодержания можно записать очевидную зависимость 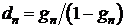
Воспользуемся законом Дальтона и запишем соотношение для удельных объемов
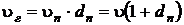 (10.7)
(10.7)
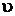 –удельный объем влажного газа, м3/кг;
–удельный объем влажного газа, м3/кг; 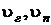 – удельные парциальные объемы сухого газа и пара в смеси, м3/кг.
– удельные парциальные объемы сухого газа и пара в смеси, м3/кг.
Или через плотности
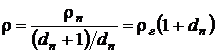 (10.8)
(10.8)
Запишем уравнение Клапейрона-Менделеева для сухого газа (воздуха) и для пара, содержащегося во влажном воздухе
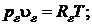
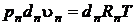 .
.
Поделим почленно второе выражение на первое и учитывая, что 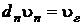 получим
получим
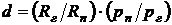 (10.9)
(10.9)
В частности, для воздуха 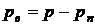 и
и 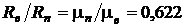 получим
получим
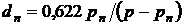 (10.10)
(10.10)
или в условиях насыщения
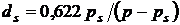 (10.11)
(10.11)
По правилу фаз Гиббса, число независимых параметров, определяющих термодинамически равновесное состояния системы 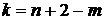 , где для влажного воздуха число компонентов
, где для влажного воздуха число компонентов 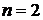 число фаз
число фаз 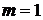 . Тогда число независимых параметров, определяющих состояние влажного газа
. Тогда число независимых параметров, определяющих состояние влажного газа 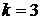 . Третий параметр должен прямо или косвенно определять концентрации компонентов.
. Третий параметр должен прямо или косвенно определять концентрации компонентов.
