Изучение работы гелий-неонового лазера

Цель работы – изучение принципа действия гелий-неонового лазера, свойств лазерного излучения, определение длины волны излучения.

Краткое теоретическое введение

Постановка задачи

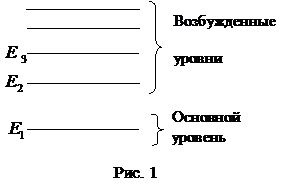Поглощение света. Спонтанное и вынужденное излучения.Согласно законам квантовой физики энергия электрона в атоме может иметь лишь определенный дискретный ряд значений: 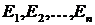. Эти значения называются «уровнями энергии». Уровень с наименьшей энергией называется основным, другие уровни, с более высокими энергиями, – возбужденными. Схема энергетических уровней атома показана на рис. 1.

При переходе электрона в атоме с одного энергетического уровня на другой атом может излучать или поглощать энергию. Эта энергия равна

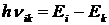. (1)

Между двумя энергетическими уровнями с энергиям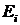и и 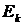возможны три типа оптических процессов (рис. 2):

1) спонтанное излучение;

2) вынужденное излучение;

3) поглощение фотонов.

Дадим их краткое описание.

1. Спонтанное излучение. Пусть атом находится в одном из возбужденных состояний с энергией 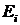. Возбужденное состояние является неустойчивым, и спустя некоторое время, 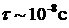, атом спонтанно (самопроизвольно) перейдет в одно из состояний с меньшей энергией 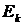с излучением фотона (рис. 2, переход 1).

Спонтанные переходы являются случайными процессами, поэтому момент испускания фотона, его направление, поляризация также случайны. Излучение обычных источников света, возникающее за счет актов спонтанного испускания, некогерентно, немонохроматично, ненаправленно, неполяризованно.

2. Вынужденное излучение. Этот вид излучения был теоретически предсказан А.Эйнштейном. Атом может перейти из возбужденного состояния 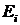в состояние с меньшей энергией 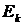не спонтанно, а под действием электромагнитного излучения (рис. 2, переход 2). Частота излучения должна удовлетворять соотношению (1).

Переходы, происходящие под действием внешнего электромагнитного излучения, называются вынужденными (индуцированными).

Отметим особенности вынужденного излучения. Фотон, излучаемый при вынужденном переходе, абсолютно неразличим с первичным фотоном, индуцировавшим этот переход. Оба фотона имеют одну и ту же частоту, фазу, поляризацию и направление движения. Эффект вынужденного излучения используется в оптических квантовых генераторах (лазерах). Лазерное излучение является вынужденным излучением. Оно монохроматично, когерентно, направленно и поляризованно.

3. Резонансное поглощение фотонов –это переходы под действием излучения из состояния с меньшей энергией 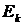в состояние с большей энергией 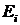при условии (1). Этот процесс является обратным вынужденному излучению (рис. 2, переход 3).

Лазеры. Квантовыми генераторами называются источники когерентного излучения, основанные на использовании эффекта вынужденного излучения. Квантовые генераторы ультракоротких радиоволн называются мазерами. Квантовые генераторы, излучающие в оптическом диапазоне, называются лазерамиилиоптическими квантовыми генераторами. Термин «лазер» является аббревиатурой (Light Amplification by Stimulated Emission of Radiation). Рассмотрим принцип работы лазера.

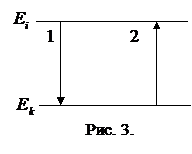Инверсия населенностей. Пусть на вещество воздействует свет частотой 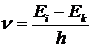.Он будет вызывать два конкурирующих процесса (рис. 3):

1 - вынужденный переход 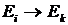(излучение); 2 - вынужденный переход (поглощение).

Вероятности этих переходов одинаковы. Обозначим 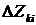- число переходов , - число переходов .

Для того чтобы получить усиление света, необходимо выполнение условия

.

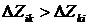Число атомов в состоянии с энергией 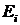называют населенностью уровня 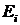и обозначают , тогда – населенность уровня 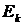. Число переходов с энергетического уровня будет пропорционально его населенности

.

Рассмотрим систему, находящуюся в состоянии термодинамического равновесия. Распределение атомов по энергетическим состояниям определится законом Больцмана

.

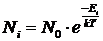Чем больше энергия уровня, тем меньше его населенность, то есть ,следовательно, число переходов с излучением будет меньше числа переходов с поглощением света. Система, находящаяся в состоянии термодинамического равновесия, не может усиливать электромагнитное излучение.

Для получения усиления света необходимо создать такое неравновесное состояние в системе, при котором населенность верхнего энергетического уровня была бы больше населенности нижнего уровня

.

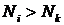Такое состояние называется состоянием с инверсией населенности. Термин “инверсия” означает обращение, переворачивание.

Необходимо отметить, что не любое возбуждение и не в каждом веществе может вызвать инверсию населенностей. Среду, в которой при определенных условиях может быть создана инверсия населенностей, называют лазерной (мазерной) активной средой, а соответствующий рабочий элемент – активным элементом. Уровни энергии, между которыми может быть создана инверсия населенностей, называют рабочими лазернымиуровнями энергии.

Способы создания инверсии населенностей. Процесс возбуждения активной среды с целью получения инверсии населенностей называют накачкой, а источник возбуждения - источником накачки. Существуют различные способы накачки. Назовем некоторые из них:

- оптическая накачка, происходит за счет поглощения вспомогательного излучения (применяется в рубиновом лазере);

- электрическая накачка – в высокочастотном газовом разряде (гелий-неоновый лазер);

- инжекция носителей заряда в область p–n – перехода (инжекционные полупроводниковые лазеры).

Практически накачка осуществляется по трехуровневой схеме, предложенной Басовым и Прохоровым (1955 г). Рассмотрим накачку на примере гелий-неонового лазера. Энергетическая диаграмма гелий-неонового лазера показана нарис.4. Активной средой в нем является плазма высокочастотного газового разряда в смеси гелия (He) и неона (Ne). Парциальные давления гелия и неона составляют, соответственно, 1мм.рт.ст и 0,1 мм.рт.ст.

Атомы гелия за счет соударения с электронами переходят из основного энергетического состояния в возбужденное состояние 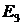(процесс 1). Состояние 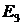является метастабильным. Это означает, что в данном состоянии атом может находиться достаточно долго: среднее время жизни составляет .

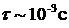За это время возбужденные атомы He при неупругих столкновениях с атомами Ne передают им свою энергию (процесс 2). В результате создается инверсная населенность энергетического уровня 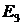атома Ne:

.

Переход атомов неона с уровня сопровождается вынужденным излучением (процесс 3). Лазерное излучение, проходя через активную среду, многократно усиливается.

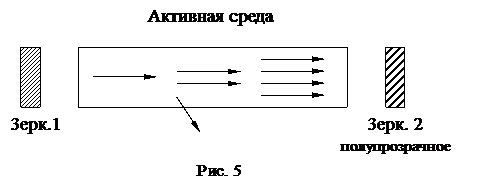Положительная обратная связь. Резонатор. Чтобы увеличить эффект усиления света и обеспечить режим генерации, активная среда помещается в резонатор. Резонатор представляет собой два зеркала, установленных параллельно друг другу (рис. 5).

Процесс генерации света заключается в следующем. Фотон, испущенный при переходе и движущийся параллельно оси резонатора, вызывает вынужденные переходы и рождает лавину фотонов, движущихся в том же направлении. Часть потока фотонов пройдет через полупрозрачное зеркало 2, часть отразится от него и пойдет в обратном направлении, продолжая усиливаться. Затем отразится от первого зеркала и т. д. При каждом проходе интенсивность света увеличивается, пока не будет достигнут установившийся режим. Фотоны, летящие под углом к оси резонатора, выходят из активной среды и в усилении не участвуют.

Принципиальная схема лазера(рис. 6). Перечислим условия, необходимые для создания и работы оптических квантовых генераторов:

1. Необходимо рабочее вещество с инверсией населенностей (активная среда).

2. Необходима положительная обратная связь (резонатор).

3. Усиление света при прохождении через активную среду должно компенсировать потери фотонов при отражении в зеркалах.

4. Необходимо, чтобы фаза волны, возвратившейся в некоторую точку после отражения от зеркал, совпадала с фазой первичной волны, т.е. должно выполняться условие

.

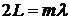Здесь 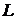– расстояние между зеркалами; 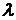– длина волны излучения; 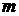– целое число. Таким образом, общая схема любого лазера имеет вид, представленный на рис. 6.

Целью данной работы является изучение принципа действия гелий-неонового лазера, свойств лазерного излучения, определение длины волны излучения. В частности, необходимо экспериментально выполнить качественную проверку монохроматичности и поляризованности лазерного излучения, определить угол расходимости лазерного луча, выполнить проверку пространственной когерентности лазерного излучения, определить длину волны лазерного излучения.

Экспериментальная часть

Задание 1. Качественная проверка монохроматичности и поляризованности лазерного излучения.

1. Установите дифракционную решетку на пути хода лазерного пучка (рис. 7), получите на экране дифракционную картину. Зарисуйте дифракционную картину (в цвете). Сделайте вывод о монохроматичности лазерного излучения.

2. Установите на оптическую скамью между лазером и экраном поляроид. Вращая поляризационную пластинку поляроида вокруг оси, совпадающей с лазерным лучом, наблюдайте картину на экране. Сделайте вывод о поляризации лазерного излучения.

Задание 2. Определение угла расходимости лазерного луча.

Одной из особенностей лазерного излучения является его острая направленность, малый угол расходимости. Это связано с тем, что в генерации и усилении света участвуют только фотоны, летящие параллельно оси резонатора. Однако волновые свойства света не позволяют получить угол расходимости,равный нулю.

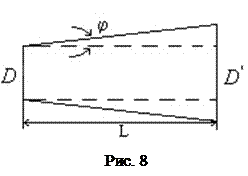
Из геометрических соображений (рис. 8) следует формула для угла расходимости

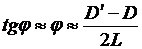, (2)

где 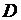– диаметр светового луча на выходе из лазера, – диаметр светлого пятна от лазерного луча на экране, 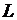– расстояние от выходного отверстия лазера до экрана. Угол расходимости лазерного луча определяет границы центрального пятна, т.е. положение первого дифракционного минимума от выходного отверстия лазера.

С другой стороны, из теории дифракции Фраунгофера на круглом отверстии положение первого минимума определяется по формуле

. (3)

Для экспериментального определения угла расходимости:

1. Получите светлое пятно лазерного луча на экране, зарисуйте его, измерьте его диаметр .

2. Измерьте диаметр светового пятна 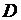на выходе из лазера. Для этого приложите миллиметровку к выходному отверстию лазера, зарисуйте круглое пятно света.

3. Измерьте расстояние 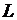от выходного отверстия лазера до экрана.

4. По формуле (2) рассчитайте угол расходимости лазерного луча.

5. По формуле (3) рассчитайте угол, под которым расположен первый дифракционный минимум от круглого отверстия диаметром .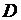

6. Сравните результаты обоих измерений, сделайте выводы.

Задание 3. Проверка пространственной когерентности лазерного излучения с помощью опыта Юнга.

Схема опыта Юнга от протяженного некогерентного источника света представлена на рис. 9. Здесь S - источник света, S^' - первая щель, которая играет роль точечного источника света. Волновой фронт от неё разделяется на два проходящих через щели S₁ и S₂. Поэтому лучи 1 и 2 когерентны между собой. Накладываясь в некоторой точке экрана, например в точке А, они или усиливают или ослабляют друг друга в зависимости от разности хода .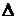

При работе с лазером необходимость щели S^' отпадает, так как излучение лазера когерентно и лучи, падающие на щели S₁ и S₂, а значит и выходящие из них, также когерентны. Лазерное излучение пространственно когерентно.

Для качественной проверки пространственной когерентности излучения лазера установите на пути луча экран с двумя щелями. Убедитесь в наличии интерференционной картины на экране. Зарисуйте эту картину. Сделайте выводы о пространственной когерентности лазерного излучения.

Задание 4. Определение длины волны лазерного излучения.

Первый способ. Дифракция на 1 щели. Условие дифракционного минимума для 1 щели

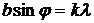, (4)

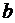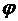где – ширина щели, – порядок минимума, - угол, под которым наблюдается минимум, - длина волны излучения.

Из геометрических соображений (рис.10) для первого минимума ( 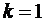) следует, что , где – координата первого интерференционного минимума, 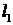- расстояние между первыми симметричными минимумами, т.е. ширина центрального максимума. При малом угле 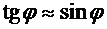и тогда

. (5)

Подставив (5) в (4), получим выражения для для :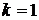

. (6)

Для экспериментального определения поместите между лазером и экраном щель шириной 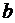. Получите дифракционную картину. Измерьте расстояние 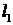между первыми симметричными минимумами, т.е. ширину центрального максимума, а также расстояние 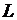. По формуле (6) определите длину волны.

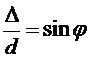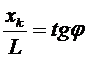Второй способ. Дифракция на двух щелях. Из геометрических соображений (рис.9) следуют соотношения и , где 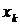- координата интерференционного максимума (или минимума), порядок которого 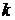, - расстояние между щелями, 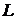- кратчайшее расстояние от щелей до экрана.

При малом угле 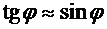, тогда , и величина оптической разности хода лучей 1 и 2, :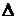

. (7)

Если в точке А наблюдается максимум, то

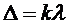. (8)

Приравняв (7) и (8), получим

.

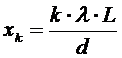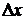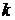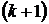Тогда расстояние между двумя соседними максимумами (или минимумами) и равно

,

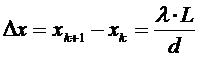откуда выражение для длины волны l

. (9)

Для экспериментального определения 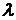измерьте на экране по дифракционной картине расстояние 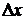между двумя соседними максимумами (или минимумами) и расстояние 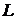от щелей до экрана. По формуле (9) рассчитайте 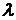. Значение дано на экране со щелями.

Сравните результаты измерений l по 1 и 2 способу. Сделайте вывод.

Задание 5. Проверка соотношения неопределенностей.

(по указанию преподавателя)

Лазерный луч – это поток фотонов. На примере дифракции от одной щели можно проверить соотношение неопределенностей:

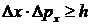, (10)

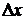где ( - постоянная Планка), - неопределенность по координате в момент прохождения фотонов через щель, – неопределенность в составляющей импульса (по оси x), возникающая из-за дифракции фотонов при прохождении щели.

Соотношение (10) для дифракции на одной щели можно получить из простых рассуждений. Неопределенность по координате 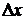равна ширине щели 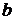, 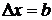. И если ограничиться только центральным максимумом, то неопределенность в составляющей импульса имеет простое выражение (схема на рис.11):

, (11)

где 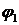- угол, соответствующий первому минимуму, 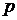– импульс фотона.

∆py

Из условия минимума для дифракции на одной щели следует, что 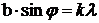или, т.к. Dx = b и для первого минимума 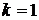, , то , и тогда

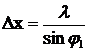. (12)

Длина волны фотона 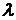связана с импульсом известным соотношением

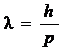. (13)

Тогда с учетом (11, 12, 13) найдем выражение для :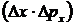

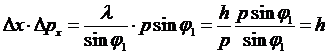, или .

Если учесть остальные максимумы, то действительно придем к неравенству (10): .

Для экспериментальной проверки соотношения неопределенностей преобразуем формулу (11). Из геометрических соображений (рис.11) следует, что 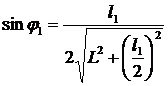, тогда с учетом (13) ,

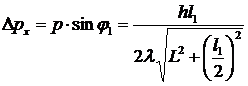т.к. 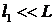, то и

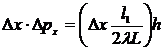. Учтя, что 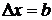, получим

. (14)

Для экспериментальной проверки соотношения неопределенности для щели заданной ширины 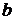получите дифракционную картину на экране на расстоянии 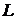. Измерьте ширину первого максимума 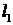_. В формулу (14) подставьте значения 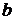, , 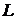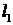и l = 660 мкм. Убедитесь в том, что полученное вами соотношение близко к . Сделайте выводы.

Контрольные вопросы

1. Каков принцип действия гелий-неонового лазера?

2. Какое излучение называется спонтанным, а какое вынужденным?

3. Что такое инверсная заселенность? Чем она достигается?

4. Как происходит усиление света в активной среде?

5. Чем обусловлена малая расходимость лазерного луча?

6. Какой процесс называют накачкой, какие существуют способы накачки?

7. Начертите трехуровневую схему лазера, покажите переходы: излучательный (лазерный), безызлучательный, накачку.

8. Начертите общую схему лазера. Какова роль активного элемента? Резонатора?

9. Как можно убедиться в пространственной когерентности лазерного излучения?

10. Как устроен резонатор? Какова его роль?

11. Каково условие дифракционного минимума от одной щели?

12. Вывести условие интерференционного максимума от двух щелей в схеме Юнга.

Список литературы

1. Трофимова Т.И. Курс физики.

2. Яворский Б.М., Детлаф А.А. Курс физики.

ЛАБОРАТОРНАЯ РАБОТА № 6-6

ОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ ПЛАНКА

Цель работы – изучение спектров испускания и поглощения,

определение постоянной Планка.