Допустимые превышения температур

При работе электрической машины часть ее энергии превращается в тепло. Это тепло выделяется в обмотках в виде электрических потерь и в виде потерь на перемагничивание стали. Кроме этого, нагреваются от трения подшипники и коллектор. Нагрев электрической машины вызывает старение изоляции, а вызванное нагревание обмоток и неодинаковые коэффициенты линейного расширения у различных частей тягового двигателя могут привести к разрыву изоляции, а значит и к преждевременному выходу машины из строя.

В связи с этим вполне естественно предположить, что на интенсивности старения изоляции будут сказываться следующие факторы:

1) значение и время действия рабочих температур;

2) пределы и частота изменения температур;

3) влажность;

4) электрическое напряжение;

5) воздействие химических элементов;

6) вибрационные нагрузки.

В настоящем подразделе будут рассматриваться первые два пункта из перечисленных.

В зависимости от нагревостойкости компонентов, входящих в состав изоляции ее подразделяют на 5 классов А, В, Е, F, Н. В тяговом электромагнитостроении используют три класса В, F, Н.

Предельные температуры нагревания для этих классов изоляции мы указывали в одном из первых разделов. Хотелось бы заметить, что расчетный срок службы изоляции класса В составляет 4…5 лет, а изоляции класса Н – 8…10 лет.

Допустимые превышения температур нормируются для каждой части тягового двигателя (обмотки якоря, обмотки полюсов, коллектора).

Таблица 7.1

Допустимые превышения температур

Класс нагревостойкости	Допустимая температура нагрева, °С
Обмотка якоря	Обмотка полюсов	Коллектор
В
F
Н

Различаются изоляционные материалы для разных классов. Для класса В – это материалы на основе слюды, асбеста и стекловолокна. Класс F– то же самое, но пропитывается синтетическими связующими и эпоксидными смолами. Класс Н – то же самое, но пропитываются кремнийорганическим составом.

7.2. Классическая теория нагревания
однородного твердого тела

Согласно этой теории части машины рассматриваются как однородные тела, выделяющие тепловую энергию. Часть этой энергии вызывает нагревание тела, а часть рассеивается в окружающую среду.

Для лучшего понимания процессов сделаем небольшой экскурс в теплотехнику и определим ряд ее аспектов и терминов. Итак, общая теплоемкость тела–количество тепла, необходимое для его нагревания на 1 °С. Общая теплоемкость зависит от массы тела m и удельной теплоемкости С

С = сm.

Общая теплоотдача тела В – количество тепловой энергии, отдаваемой за единицу времени со всей поверхности в окружающую среду при разности температур в 1 °С

,

где 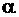– коэффициент теплоотдачи Вт/см²; S – площадь поверхности тела.

Коэффициент теплоотдачи – количество тепловой энергии, отдаваемой лучеиспусканием и конвенцией за единицу времени с единицы поверхности тела при разности температур в 1 °С.

Представим, что в начале испытания температура тела равна температуре окружающей среды, тогда за начальную единицу времени выделится тепловая энергия . За какое-то время dt выделится энергия . Причем она будет делиться на две составляющие:

Часть её пойдет на нагревание тела , а другая на рассеивание в окружающую среду.

Если за время dt температура тела повысилась на , то на это затрачена тепловая энергия

.

Так как тепловая энергия частью поглощается телом, а частью рассеивается, то можно записать уравнение теплового баланса

.

Хотелось бы сразу пояснить два момента.

Во-первых, если в начале нагревания температура тела равна температуре окружающей среды т. е. , то

.

Вся выделившаяся энергия будет затрачиваться на нагревание тела. И наоборот, если величина постоянная, то через некоторое время тело настолько нагреется, что вся выделившаяся энергия будет рассеиваться в окружающую среду, то есть , тогда d и

.

Отсюда, установившееся превышение температуры тела

.

Учитывая, что выделившийся в теле тепловой поток

,

запишем

.

Разделив правую и левую часть на В и обозначив , получим

,

где Т – постоянная времени нагревания, т. е. это время, за которое превышение температуры рассматриваемого тела над температурой окружающей среды достигнет при отсутствии теплоотдачи в окружающую среду.

Разделив переменные, получим

,

интегрируя, получим

,

где N – постоянная интегрирования.

При t = 0

,

тогда

или

.

Определим из полученного выражения, превышение температуры тела над температурой окружающей среды в функции времени

;

;

. (4)

Если начальное превышение температуры тела , тогда

.

Исходя из этого кривые нагревания и охлаждения однородного тела будут иметь вид, показанный на рис. 7.1.

Рис. 7.1. Кривые нагревания и охлаждения однородного тела: 1, 2 – кривые намагничивания; 3 – кривая охлаждения

Учитывая что можно сказать, что, если тепловыделение прекратилось, т. е. , то уравнение приобретает вид

.

Этому уравнению соответствует на рис. 7.1 кривая (3) охлаждения тела. Это наиболее общее уравнение, характеризующее нагревание тела. Теперь рассмотрим процесс нагревания, для примера, одной из обмоток. Остальные обмотки рассчитывают аналогично.