Равновесный состав реагирующей смеси

Концентрации всех компонентов в реагирующей смеси связаны между собой стехиометрическим уравнением, их можно определить через начальный состав и степень превращения ключевого компонента x.

В равновесии достигается равновесная степень превращения xр, так что выражение (2) или (3) примет вид

КР = f(xР) (4

Определив из него xр, далее находят равновесные концентрации всех компонентов. Приведем примеры.

Простая реакция.

•Простая обратимая реакция: А = R.

Начальная концентрация компонента А - С_A0, компонент R - отсутствует.

В равновесном состоянии С_А,равн= c_A0(1-x_Р)

и С_R,равн= С_A0x_Р.

Из (2) получим

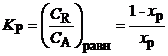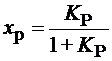, (5)

Учитывая зависимость К_Р(Т) для экзо- и эндотермических реакций, можно построить зависимость x_Р(Т) для этих реакций - рис. 3.3.

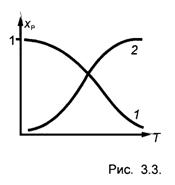
2. Конверсия СО с водяным паром: СО + Н2О = СО2 + Н2. Для нее

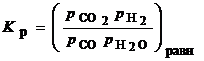
где парциальные давления компонентов pi = РСi;

Р - общее давление.

Концентрации СО, Н₂О, СО₂, Н2 в начальной смеси С₁₀, С₂₀, С₃₀, С₄₀, а в равновесии - С₁р, С₂р, С₃р, С₄р соответственно.

Выразим Сip через равновесную степень превращения xP:

С₁р = С₁₀(1 - x_Р); С₂р = С₂₀ - С₁₀Х_Р; С₃р = С₃₀ + С₁₀X_Р; С₄р = С₄₀ + С₁₀X_Р;

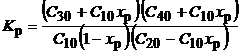
тогда из (3.39) получим квадратное уравнение относительно xP:

Его решение

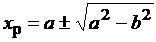
где а = К_Р/[2С₁₀(К_Р - 1)], b = (С₂₀/С₁₀) [К_Р - С₃₀С₄₀/(С₁₀С₂₀)]. (0 < X_Р < 1)

3. Не всегда можно получить аналитическое выражение для xр.

Реакция SO₂ + 0,5O₂ = SO₃ протекает с изменением объема.

Начальные концентрации SO₂ и O₂ - С₁₀ и С₂₀ соответственно.

Парциальные давления компонентов получим из определения pi = РСi

Р - общее давление.

Концентрации компонентов выразим через степень превращения SO₂ - x:

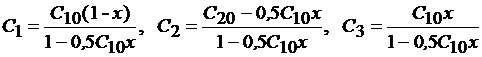
(индекс "3" относится к SO₃).

В условиях равновесия

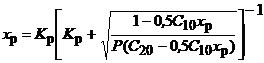
Уравнение решают методом подбора xр, после чего находят концентрации всех компонентов.

Сложная реакция

Для расчета равновесного состава смеси, в которой протекает сложная реакция, описываемая несколькими уравнениями, надо использовать только стехиометрически независимые уравнения как при расчете состава реагирующей смеси .Возможная последовательность расчета такая.

1. Определяется базисная система стехиометрически независимых уравнений, позволяющая выразить концентрации всех компонентов смеси через степени превращения ключевого вещества в каждом уравнении выбранной системы.

Обозначим их C(x). Число определенных степеней превращения и количество уравнений в базисной системе совпадают.

Например, для конверсии метана определена базисная система уравнений

CН4 + Н2О = СО + 3Н2;

СН4 + 2Н2О = СO2 + 4Н2.

и получены выражения для концентраций всех веществ, т.е. C(x).

2. Сложное превращение может быть представлено протекающими реакциями, не обязательно совпадающими с уравнениями для расчета состава реагирующей смеси, но их число такое же, как в базисной системе уравнений. Для этих уравнений известны константы равновесия, и можно определить уравнения равновесия. Обозначим их KPj(C).

В примере конверсии метана такими реакциями являются реакции

CН4 + Н2О = СО + 3Н2;

СО + Н2О = СО2 + Н2,

и химическое равновесие - KP(C) - определяется уравнениями:

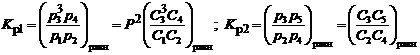
где КР1, КР2 – константы равновесия; р1, р2, р3, р4, р5 – равновесные парциальные давления соответственно CН4, Н2О, Н2, СО, СО2; Сi – соответствующие концентрации (мольные доли).

3. Полученные зависимости C(x) подставляем в выражения K_Pj(C) и получаем зависимости K_Pj(х), в которых x становятся равновесными степенями превращения X_Р, т.е. получаем зависимости K_P(X_Р). Для заданных условий (температура, давление) определяем константы равновесия реакций, и из уравнений K_P(X_Р) определяем все значения X_P. Теперь из имеющихся зависимостей C(x) можно рассчитать равновесный состав реакционной смеси – концентрации всех компонентов.

Изменение химического равновесия достигается изменением внешних условий. Направленность влияния определяется правилом, называемом принципом Ле-Шателье: